Giải Toán 9 trang 95 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 95 Tập 2 trong Bài 3: Hình cầu Toán 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 95.

Giải Toán 9 trang 95 Tập 2 Chân trời sáng tạo

Vận dụng 1 trang 95 Toán 9 Tập 2: Gấp chiếc đèn trang trí dạng hình cầu (mặt cầu) theo hướng dẫn sau:

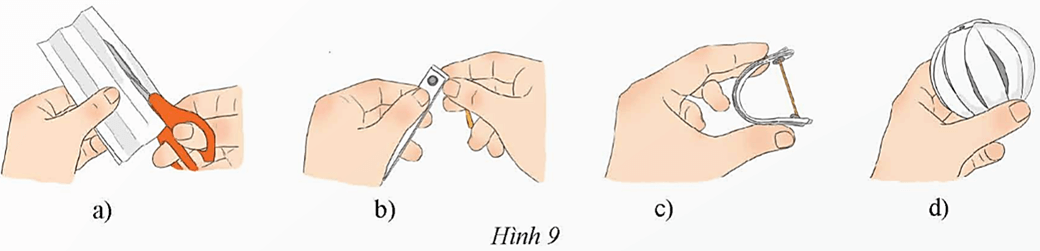
− Cắt các mảnh giấy hình chữ nhật có chiều dài 20 cm, chiều rộng 1 cm (Hình 9a).

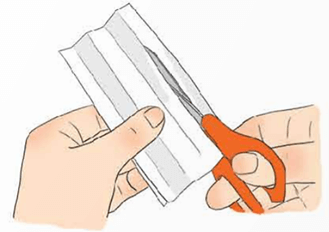
− Đục lỗ rồi dùng nút gắn vào nhau (Hình 9b).

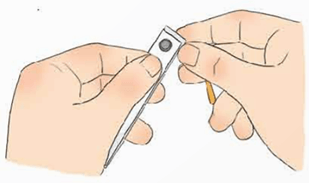
− Cố định hai lỗ bằng que tre có độ dài bằng $\frac{2x}{\pi }$ (khoảng 0,6x) với x là khoảng cách giữa hai cái lỗ (Hình 9c).

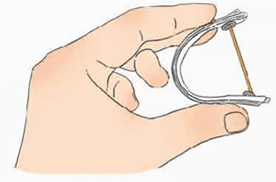
− Tách các mảnh giấy ra và trải đều, hình được tạo thành có dạng hình cầu (Hình 9d).

Lời giải:

HS thực hành theo các bước như trong Hình 9 như sau:

Bước 1: Cắt các mảnh giấy hình chữ nhật có chiều dài 20 cm, chiều rộng 1 cm.

Bước 2: Đục lỗ rồi dùng nút gắn vào nhau.

Bước 3: Cố định hai lỗ bằng que tre có độ dài bằng $\frac{2x}{\pi }$ (khoảng 0,6x) với x là khoảng cách giữa hai cái lỗ.

Bước 4: Tách các mảnh giấy ra và trải đều, hình được tạo thành có dạng hình cầu.

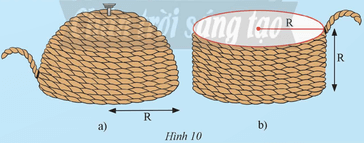
Khám phá 3 trang 95 Toán 9 Tập 2: Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R.

a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b.

b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.

Lời giải:

a) Diện tích xung quanh của phần hình trụ là: S = 2πR . R = 2πR².

Vậy diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b là 2πR².

b) Theo đề bài, chiều cao của phần hình trụ được quấn dây bằng bán kính R.

Dự đoán: Diện tích nửa mặt cầu là 2πR².

Lời giải bài tập Toán 9 Bài 3: Hình cầu hay khác:

• Giải Toán 9 trang 93

• Giải Toán 9 trang 94

• Giải Toán 9 trang 96

• Giải Toán 9 trang 97