Giải Toán 9 trang 10 Tập 2 Kết nối tri thức
Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 10 Tập 2 trong Bài 19: Phương trình bậc hai một ẩn Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 10.
Giải Toán 9 trang 10 Tập 2 Kết nối tri thức
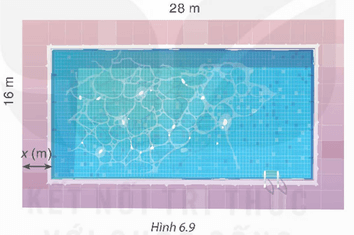
Mở đầu trang 10 Toán 9 Tập 2: Trên một mảnh đất hình chữ nhật có kích thước 28 m × 16 m, người ta dự định làm một bể bơi có đường đi xung quanh (H.6.9). Hỏi bề rộng của đường đi là bao nhiêu để diện tích của bể bơi là 288 m2?
Lời giải:
Sau bài học này, chúng ta sẽ giải được bài toán trên như sau:
Theo bài, ta có điều kiện của x là 0 < x < 8.
Chiều dài của bể bơi là: 28 – x – x = 28 – 2x (m).
Chiều rộng của bể bơi là: 16 – x – x = 16 – 2x (m).
Diện tích của bể bơi theo x là:
S = (28 – 2x)(16 – 2x) = 448 – 56x – 32x + 4x2 = 4x2 – 88x + 448 (m2).
Theo bài, S = 288 m2 nên ta có phương trình: 4x2 – 88x + 448 = 288.
Giải phương trình:
4x2 – 88x + 448 = 288
4x2 – 88x + 160 = 0
x2 – 22x + 40 = 0.
Phương trình trên có a = 1; b’ = –11; c = 40 và ∆’ = (–11)2 – 1.40 = 81 nên
Do đó, phương trình trên có hai nghiệm phân biệt và
Ta thấy chỉ có x = 2 thỏa mãn điều kiện 0 < x < 16.
Vậy bề rộng của đường đi là 2 mét để diện tích của bể bơi là 288 m2.
HĐ1 trang 10 Toán 9 Tập 2: Xét bài toán trong tình huống mở đầu.
Gọi x (m) là bề rộng của mặt đường (0 < x < 8). Tính chiều dài và chiều rộng của bể bơi theo x.
Lời giải:
Chiều dài của bể bơi là: 28 – x – x = 28 – 2x (m).
Chiều rộng của bể bơi là: 16 – x – x = 16 – 2x (m).
HĐ2 trang 10 Toán 9 Tập 2: Dựa vào kết quả HĐ1, tính diện tích của bể bơi theo x.
Lời giải:
Diện tích của bể bơi theo x là:
S = (28 – 2x)(16 – 2x) = 448 – 56x – 32x + 4x2 = 4x2 – 88x + 448 (m2).
HĐ3 trang 10 Toán 9 Tập 2: Sử dụng giả thiết và kết quả HĐ2, hãy viết phương trình để tìm x.
Lời giải:
Theo bài, diện tích của bể bơi là S = 288 m2 nên ta có phương trình:
4x2 – 88x + 448 = 288
4x2 – 88x + 160 = 0.
Lời giải bài tập Toán 9 Bài 19: Phương trình bậc hai một ẩn hay khác: