Giải Toán 9 trang 16 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 16 Tập 2 trong Bài 19: Phương trình bậc hai một ẩn Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 16.

Giải Toán 9 trang 16 Tập 2 Kết nối tri thức

Luyện tập 7 trang 16 Toán 9 Tập 2: Sử dụng máy tính cầm tay, tìm nghiệm của các phương trình sau:

a) $5x^2+2\sqrt{10}x+2=0;$

b) 3x² – 5x + 7 = 0;

c) 4x² – 11x + 1 = 0.

Lời giải:

Với mỗi loại máy tính cầm tay, sau khi mở máy ta bấm phím để chuyển về chế độ giải phương trình bậc hai.

Tiếp theo, với từng phương trình ta thực hiện như sau:

Tìm nghiệm của phương trình	Bấm phím	Màn hình hiện	Kết luận
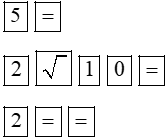$5x^2+2\sqrt{10}x+2=0$			Phương trình có nghiệm kép: $x_1=x_2=-\frac{\sqrt{10}}{5}.$
3x2 – 5x + 7 = 0		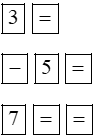Bấm tiếp phím	Phương trình vô nghiệm.
4x2 – 11x + 1 = 0		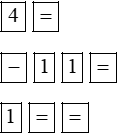Bấm tiếp phím	Phương trình có hai nghiệm phân biệt: $x_1=\frac{11+\sqrt{105}}{8};$ $x_2=\frac{11-\sqrt{105}}{8}.$

Bài 6.8 trang 16 Toán 9 Tập 2: Đưa các phương trình sau về dạng ax² + bx + x = 0 và xác định các hệ số a, b, c của phương trình đó.

a) 3x² + 2x – 1 = x² – x;

b) (2x + 1)² = x² + 1.

Lời giải:

a) 3x² + 2x – 1 = x² – x

3x² – x² + 2x + x – 1 = 0

2x² + 3x – 1 = 0

Phương trình trên có a = 2, b = 3 và c = –1.

b) (2x + 1)² = x² + 1

4x² + 4x + 1 – x² – 1 = 0

3x² + 4x = 0.

Phương trình trên có a = 3, b = 4 và c = 0.

Bài 6.9 trang 16 Toán 9 Tập 2: Giải các phương trình sau:

a) $2x^2+\frac{1}{3}x=0;$

b) (3x + 2)² = 5.

Lời giải:

a) $2x^2+\frac{1}{3}x=0$

$x\left(2x+\frac{1}{3}\right)=0$

x = 0 hoặc $2x+\frac{1}{3}=0$

x = 0 hoặc $2x=-\frac{1}{3}$

x = 0 hoặc $x=-\frac{1}{6}.$

vậy phương trình có hai nghiệm x₁ = 0, $x_2=-\frac{1}{6}.$

b) (3x + 2)² = 5.

3x + 2 = $\sqrt{5}$ hoặc 3x + 2 = -$\sqrt{5}$

3x = -2 + $\sqrt{5}$ hoặc 3x = -2-$\sqrt{5}$

$x=\frac{-2+\sqrt{5}}{3}$ hoặc $x=\frac{-2-\sqrt{5}}{3}.$

Vậy phương trình có hai nghiệm $x_1=\frac{-2+\sqrt{5}}{3},$ $x_2=\frac{-2-\sqrt{5}}{3}.$

Bài 6.10 trang 16 Toán 9 Tập 2: Không cần giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức ∆ và xác định số nghiệm của mỗi phương trình sau:

a) 11x² + 13x – 1 = 0;

b) 9x² + 42x + 49 = 0;

c) x² – 2x + 3 = 0.

Lời giải:

a) 11x² + 13x – 1 = 0

Ta có a = 11, b = 13, c = –1 và ∆ = 13² – 4.11.(–1) = 213 > 0.

Vậy phương trình trên có hai nghiệm phân biệt.

b) 9x² + 42x + 49 = 0

Ta có a = 9, b = 42, c = 49 và ∆ = 42² – 4.9.49 = 0.

Vậy phương trình trên có nghiệm kép.

c) x² – 2x + 3 = 0

Ta có a = 1, b = –2, c = 3 và ∆ = (–2)² – 4.1.3 = –8 < 0.

Vậy phương trình vô nghiệm (không có nghiệm).

Lời giải bài tập Toán 9 Bài 19: Phương trình bậc hai một ẩn hay khác:

• Giải Toán 9 trang 10

• Giải Toán 9 trang 11

• Giải Toán 9 trang 12

• Giải Toán 9 trang 13

• Giải Toán 9 trang 14

• Giải Toán 9 trang 15

• Giải Toán 9 trang 17