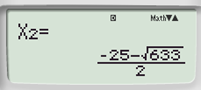Giải Toán 9 trang 17 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 17 Tập 2 trong Bài 19: Phương trình bậc hai một ẩn Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 17.

Giải Toán 9 trang 17 Tập 2 Kết nối tri thức

Bài 6.11 trang 17 Toán 9 Tập 2: Dùng công thức nghiệm của phương trình bậc hai, giải các phương trình sau:

a) $x^2-2\sqrt{5}x+2=0;$

b) 4x² + 28x + 49 = 0;

c) $3x^2-3\sqrt{2}x+1=0.$

Lời giải:

a) $x^2-2\sqrt{5}x+2=0$

Ta có $\Delta ={\left(-2\sqrt{5}\right)}^2-4\cdot 1\cdot 2=12>0$ và $\sqrt{\Delta }=\sqrt{12}=2\sqrt{3}.$

Do đó phương trình có hai nghiệm phân biệt:

$x_1=\frac{2\sqrt{5}+2\sqrt{3}}{2}=\sqrt{5}+\sqrt{3},$ $x_2=\frac{2\sqrt{5}-2\sqrt{3}}{2}=\sqrt{5}-\sqrt{3}.$

b) 4x² + 28x + 49 = 0

Ta có $\Delta$ = 28² -4.4.49 = 0.

Do đó phương trình có nghiệm kép:

$x_1=x_2=-\frac{28}{2\cdot 4}=-\frac{7}{2}.$

c) $3x^2-3\sqrt{2}x+1=0$

Ta có $\Delta ={\left(-3\sqrt{2}\right)}^2-4\cdot 3\cdot 1=6>0.$

Do đó phương trình có hai nghiệm phân biệt:

$x_1=\frac{3\sqrt{2}+\sqrt{6}}{6},$ $x_2=\frac{3\sqrt{2}-\sqrt{6}}{6}.$

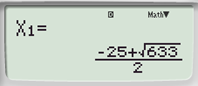
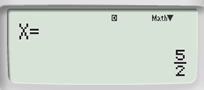
Bài 6.12 trang 17 Toán 9 Tập 2: Sử dụng máy tính cầm tay, tìm nghiệm của các phương trình sau:

a) 0,1x² + 2,5x – 0,2 = 0;

b) 0,01x² – 0,05x + 0,0625 = 0;

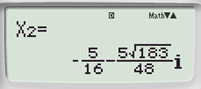
c) 1,2x² + 0,75x + 2,5 = 0.

Lời giải:

Với mỗi loại máy tính cầm tay, sau khi mở máy ta bấm phím để chuyển về chế độ giải phương trình bậc hai.

Tiếp theo, với từng phương trình ta thực hiện như sau:

Tìm nghiệm của phương trình	Bấm phím	Màn hình hiện	Kết luận
0,1x2 + 2,5x – 0,2 = 0		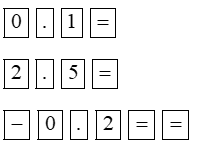Bấm tiếp phím	Phương trình có hai nghiệm phân biệt: $x_1=\frac{-25+\sqrt{633}}{2};$ $x_2=\frac{-25-\sqrt{633}}{2}.$
0,01x2 – 0,05x + 0,0625 = 0		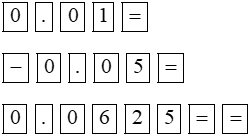	Phương trình có nghiệm kép: $x_1=x_2=\frac{5}{2}.$
1,2x2 + 0,75x + 2,5 = 0		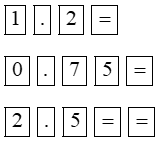Bấm tiếp phím	Phương trình vô nghiệm.

Bài 6.13 trang 17 Toán 9 Tập 2: Độ cao h (mét) so với mặt đất của một vật được phóng thẳng đứng lên trên từ mặt đất với vận tốc ban đầu v₀ = 19,6 m/s cho bởi công thức h = 19,6t – 4,9t², ở đó t là thời gian kể từ khi phóng (giây) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016). Hỏi sau bao lâu kể từ khi phóng, vật sẽ rơi trở lại mặt đất?

Lời giải:

Khi vật rơi trở lại mặt đất, độ cao h = 0 hay 19,6t – 4,9t² = 0 với t > 0.

Giải phương trình:

19,6t – 4,9t² = 0

t(19,6 – 4,9t) = 0

t = 0 hoặc 19,6 – 4,9t = 0

t = 0 hoặc 4,9t = 19,6

t = 0 hoặc t = 4

Ta thấy chỉ có giá trị t = 4 thỏa mãn điều kiện t > 0.

Vậy kể từ khi phóng sau 4 giây vật sẽ rơi trở lại mặt đất.

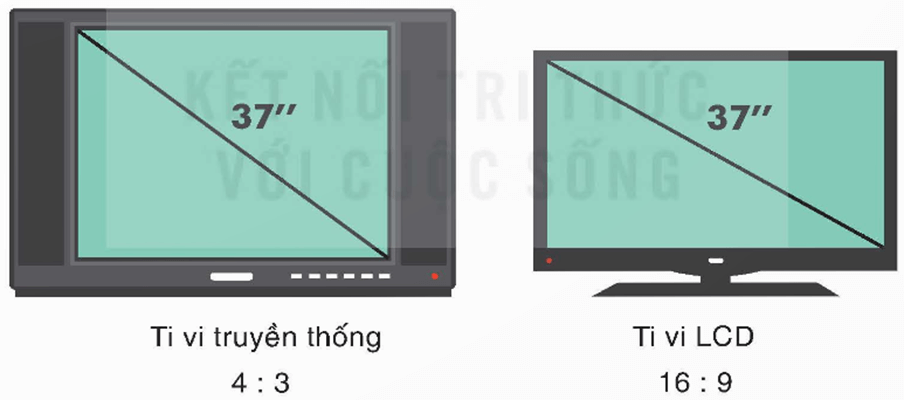
Bài 6.14 trang 17 Toán 9 Tập 2: Kích thước màn hình ti vi hình chữ nhật được xác định bằng độ dài đường chéo. Ti vi truyền thống có định dạng 4 : 3, nghĩa là tỉ lệ giữa chiều dài và chiều rộng của màn hình là 4 : 3. Hỏi diện tích của màn hình ti vi truyền thống 37 in là bao nhiêu? Diện tích của màn hình ti vi LCD 37 in có định dạng 16 : 9 là bao nhiêu? Màn hình ti vi nào có diện tích lớn hơn? Ở đây, các diện tích của màn hình được tính bằng inch vuông.

Lời giải:

Tỉ lệ giữa chiều dài và chiều rộng là 4 : 3, gọi chiều dài là 4x (in) thì chiều rộng là 3x (in) (x > 0).

Theo định lí Pythagore, ta có:

(3x)² + (4x)² = 37²

9x² + 16x² = 1 369

25x² = 1 369

x² = 54,76

x = 7,4 hoặc x = –7,4.

Ta thấy chỉ có x = 7,4 thỏa mãn điều kiện x > 0.

Diện tích của màn hình ti vi truyền thống 37 in là:

4x . 3x = 12x² = 12 . 54,76 = 657,12 (in²).

Tương tự, tỉ lệ giữa chiều dài và chiều rộng là 16 : 9, gọi chiều dài là 16y (in) thì chiều rộng là 9y (in) (y > 0).

Theo định lí Pythagore, ta có:

(9x)² + (16x)² = 37²

81x² + 256x² = 1 369

337x² = 1 369

$x^2=\frac{1369}{337}.$

Diện tích của màn hình ti vi LCD 37 in là:

$16x\cdot 9x=144x^2=144\cdot \frac{1369}{337}\approx 585$ (in²).

Ta thấy 657,12 > 585.

Do đó, màn hình ti vi truyền thống có diện tích lớn hơn.

Bài 6.15 trang 17 Toán 9 Tập 2: Một mảnh vườn hình chữ nhật có chiều rộng ngắn hơn chiều dài 6 m và có diện tích là 280 m². Tính các kích thước của mảnh vườn đó.

Lời giải:

Gọi chiều rộng mảnh vườn hình chữ nhật là x (m) (x > 0).

Chiều rộng ngắn hơn chiều dài 6 m nên chiều dài mảnh vườn là x + 6 (m).

Diện tích mảnh vườn là: x(x + 6) (m²).

Theo bài, mảnh vườn có diện tích là 280 m² nên ta có phương trình:

x(x + 6) = 280.

x² + 6x – 280 = 0.

Ta có ∆’ = 3² – 1.(–280) = 289 > 0 và $\sqrt{289}=17.$

Do đó, phương trình có hai nghiệm phân biệt:

x₁ = –3 + 17 = 14, x₂ = –3 – 17 = –20.

Ta thấy chỉ có giá trị x₁ = 14 thỏa mãn điều kiện x > 0.

Vậy chiều rộng mảnh vườn là 14 m và chiều dài mảnh vườn là 14 + 6 = 20 (m).

Lời giải bài tập Toán 9 Bài 19: Phương trình bậc hai một ẩn hay khác:

• Giải Toán 9 trang 10

• Giải Toán 9 trang 11

• Giải Toán 9 trang 12

• Giải Toán 9 trang 13

• Giải Toán 9 trang 14

• Giải Toán 9 trang 15

• Giải Toán 9 trang 16