Lý thuyết Ôn tập chương 2 Đại Số hay, chi tiết - Toán lớp 10

---

Lý thuyết Ôn tập chương 2 Đại Số hay, chi tiết

Tài liệu Lý thuyết Ôn tập chương 2 Đại Số hay, chi tiết Toán lớp 10 sẽ tóm tắt kiến thức trọng tâm về chương 2 Đại Số từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 10.

HÀM SỐ

I. SỰ BIẾN THIÊN CỦA HÀM SỐ

1. Ôn tập

Hàm số y = f(x) gọi là đồng biến (tăng) trên khoảng (a ; b) nếu

∀x₁, x₂ ∈ (a ; b) : x₁ < x₂ => f(x₁) < f(x₂)

Hàm số y = f(x) gọi là nghịch biến (giảm) trên khoảng (a ; b) nếu

2. Bảng biến thiên

Xét chiều biến thiên của một hàm số là tìm các khoảng đồng biến và các khoảng nghịch biến của nó. Kết quả xét chiều biến thiên được tổng kết trong một bảng gọi là bảng biến thiên.

Nhìn vào bảng biến thiên, ta sơ bộ hình dung được đồ thị hàm số (đi lên trong khoảng nào, đi xuống trong khoảng nào).

II. TÍNH CHẴN LẺ CỦA HÀM SỐ

1. Hàm số chẵn, hàm số lẻ

Hàm số với tập xác định gọi là hàm số chẵn nếu

∀x ∈ D thì -x ∈ D và f(x) = f(-x)

Hàm số với tập xác định gọi là hàm số lẻ nếu

∀x₁, x₂ ∈ (a ; b) : x₁ < x₂ => f(x₁) > f(x₂)

2. Đồ thị của hàm số chẵn, hàm số lẻ

Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.

Đồ thị của một hàm số lẻ nhận gốc tọa độ là tâm đối xứng.

HÀM SỐ y = ax + b

I. ÔN TẬP VỀ HÀM SỐ BẬC NHẤT

y = ax + b ( a ≠ 0 ).

Tập xác định D = R

Chiều biến thiên

Với a > 0 hàm số đồng biến trên

Với a < 0 hàm số nghịch biến trên

Bảng biến thiên

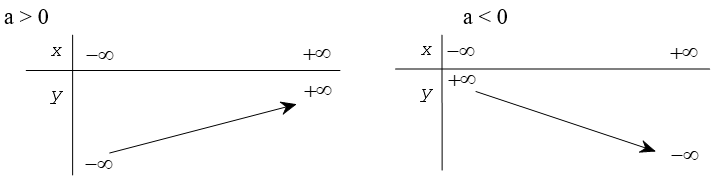
Đồ thị

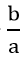
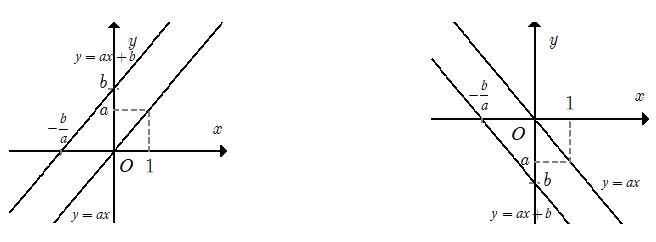
Đồ thị của hàm số là một đường thẳng không song song và cũng không trùng với các trục tọa độ. Đường thẳng này luôn song song với đường thẳng y = ax (nếu b ≠ 0) và đi qua hai điểm A(0 ; b), B( - ; 0).

II. HÀM SỐ HẰNG y = b

Đồ thị hàm số y = b là một đường thẳng song song hoặc trùng với trục hoành và cắt trục tung tại điểm (0 ; b). Đường thẳng này gọi là đường thẳng y = b.

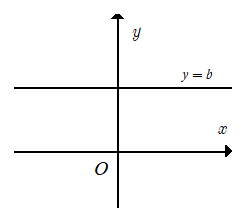
III. HÀM SỐ y = |x|

Hàm số y = |x| có liên quan chặt chẽ với hàm bậc nhất.

1. Tập xác định

Hàm số y = |x| xác định với mọi giá trị của x ∈ R tức là tập xác định y = |x|

2. Chiều biến thiên

Theo định nghĩa của giá trị tuyệt đối, ta có

Từ đó suy ra hàm số nghịch biến trên khoảng và đồng biến trên khoảng

Bảng biến thiên

Khi và dần tới thì dần tới khi dần tới thì cũng dần tới Ta có bảng biến thiên sau

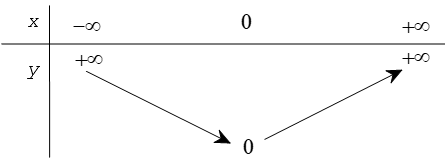
3. Đồ thị

Trong nửa khoảng đồ thị của hàm số trùng với đồ thị của hàm số Trong khoảng đồ thị của hàm số trùng với đồ thị của hàm số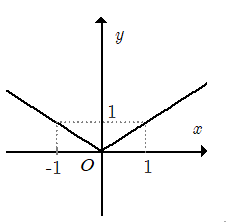

HÀM SỐ BẬC HAI

I. ĐỒ THỊ CỦA HÀM SỐ BẬC HAI

Đồ thị của hàm số là một đường parabol có đỉnh là điểm có trục đối xứng là đường thẳng Parabol này quay bề lõm lên trên nếu xuống dưới nếu

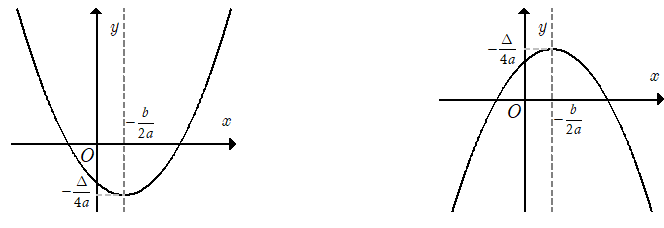
Cách vẽ

Để vẽ parabol ta thực hiện các bước

1) Xác định tọa độ của đỉnh

2) Vẽ trục đối xứng

3) Xác định tọa độ các giao điểm của parabol với trục tung (điểm ) và trục hoành (nếu có).

Xác định thêm một số điểm thuộc đồ thị, chẳng hạn điểm đối xứng với điểm qua trục đối xứng của parabol, để vẽ đồ thị chính xác hơn.

4) Vẽ parabol.

Khi vẽ parabol cần chú ý đến dấu của hệ số ( bề lõm quay lên trên, bề lõm quay xuống dưới).

II. CHIỀU BIẾN THIÊN CỦA HÀM SỐ BẬC HAI

Dựa vào đồ thị hàm số ta có bảng biến thiên của nó trong hai trường hợp và như sau

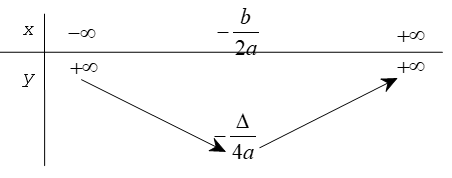
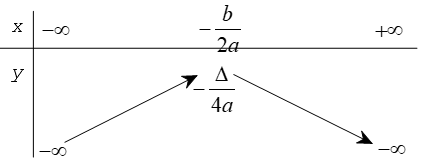
Từ đó, ta có định lí dưới đây

Định lí

Nếu thì hàm số nghịch biến trên khoảng đồng biến trên khoảng

Nếu thì hàm số đồng biến trên khoảng nghịch biến trên khoảng