Top 150 Đề thi Toán 10 Cánh diều có đáp án

---

Haylamdo biên soạn và sưu tầm 100 Đề thi Toán lớp 10 Cánh diều năm học 2023 mới nhất đầy đủ Học kì 1 và Học kì 2 gồm đề thi giữa kì, đề thi học kì có đáp án chi tiết, cực sát đề thi chính thức giúp học sinh ôn luyện & đạt điểm cao trong các bài thi Toán 10.

Mục lục Đề thi Toán lớp 10 Cánh diều năm 2023 mới nhất

Xem thử

Chỉ 200k mua trọn bộ Đề thi Toán 10 Cánh diều (cả năm) bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

- Đề thi Toán 10 Giữa kì 1 Cánh diều

• Đề thi Giữa kì 1 Toán lớp 10 Cánh diều có đáp án (4 đề)

  Xem đề thi

- Đề thi Toán 10 Học kì 1 Cánh diều

• Đề thi Học kì 1 Toán lớp 10 Cánh diều có đáp án (4 đề)

  Xem đề thi

- Đề thi Toán 10 Giữa kì 2 Cánh diều

• Đề thi Giữa kì 2 Toán 10 Cánh diều có đáp án (4 đề)

  Xem đề thi

- Đề thi Toán lớp 10 Học kì 2

• Đề thi Học kì 2 Toán lớp 10 Cánh diều có đáp án (4 đề)

  Xem đề thi

Xem thêm đề thi Toán 10 cả ba sách:

• Top 20 Đề thi Giữa kì 1 Toán lớp 10 năm học 2023 có đáp án (cả ba sách)

  Xem đề thi

• Top 20 Đề thi Học kì 1 Toán 10 năm học 2023 có đáp án (cả ba sách)

  Xem đề thi

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Cánh diều

Năm học 2023

Môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 1)

I. PHẦN TRẮC NGHIỆM

Câu 1: Trong các câu dưới đây, câu nào là mệnh đề ?

A. Hà Nội là thủ đô của Việt Nam.

B. Hôm nay là thứ mấy ?

C. Mệt quá !

D. Mấy giờ rồi ?

Câu 2: Trong các mệnh đề dưới đây, mệnh đề nào đúng ?

A. 5 là số tự nhiên chẵn;

B. 5 là số nguyên tố;

C. 5 là số nguyên âm;

D. 5 là số chia hết cho 3.

Câu 3: Cho tập hợp A = {1; 3; 5; 7; 9}. Số phần tử của tập hợp A là

A. 6;

B. 4;

C. 5;

D. 3.

Câu 4: Cho tập hợp B = $\left\{\left.x\in ℝ\right|a\le x<b\right\}$. Mệnh đề nào dưới đây đúng ?

A. B = [a; b];

B. B = (a; b];

C. B = [a; b) ;

D. B = (a; b).

Câu 5: Tập xác định của hàm số f(x)= $\sqrt{x-2}$ là

A. D = [2; +∞);

B. D = (2; +∞);

C. D = (– ∞; 2);

D. D = (– ∞; 2].

Câu 6: Trong mặt phẳng Oxy, điểm nào dưới đây thuộc đồ thị của hàm số y=$\sqrt{x}$ ?

A. P(4; 2);

B. M(1; – 1);

C. N(2; 4);

D. Q(2; – 4).

Câu 7: Cho hàm số f(x) = x³ – 2. Giá trị f(1) bằng bao nhiêu?

A. 3;

B. – 1;

C. 2;

D. 1

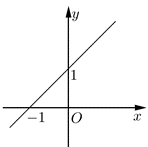
Câu 8: Hàm số nào dưới đây có đồ thị là đường thẳng như trong hình bên ?

A. y = x + 1;

B. y = x – 1;

C. y = – x + 1;

D. y = – x – 1.

Câu 9: Trong các mệnh đề dưới đây, mệnh đề nào đúng ?

A. Đồ thị hàm số chẵn nhận đường thẳng y = x làm trục đối xứng.

B. Đồ thị hàm số chẵn nhận trục hoành làm trục đối xứng.

C. Đồ thị hàm số chẵn nhận nhận đường thẳng y = – x làm trục đối xứng.

D. Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.

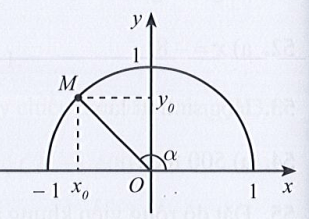
Câu 10: Trong mặt phẳng Oxy, biết điểm M(2; y₀) thuộc đồ thị của hàm số y = 2x – 3. Giá trị của y₀ bằng:

A. 2;

B. 0;

C. – 1;

D. 1.

Câu 11: Trong mặt phẳng Oxy đồ thị của hàm số y = x² – 2x + 3 có trục đối xứng là đường thẳng nào dưới đây ?

A. x = 1;

B. x = – 1;

C. x = 2;

D. x = – 2.

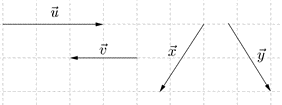
Câu 12: Cho các vectơ $\overrightarrow{u},\overrightarrow{v},\overrightarrow{x},\overrightarrow{y}$ như trong hình:

Mệnh đề nào dưới đây là đúng?

A. Hai vectơ $\overrightarrow{x}$ và $\overrightarrow{y}$ cùng hướng;

B. Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ cùng hướng;

C. Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ ngược hướng;

D. Hai vectơ $\overrightarrow{x}$ và $\overrightarrow{y}$ ngược hướng.

Câu 13: Vectơ có điểm đầu là A và điểm cuối là B được kí hiệu là:

A. AB;

B. BA;

C. $\overrightarrow{AB}$

D. $\overrightarrow{BA}$

Câu 14: Cho I là trung điểm của đoạn thẳng AB và M là một điểm tùy ý. Mệnh đề nào dưới đây đúng?

A. $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{IM}.$

B. $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MI}.$

C. $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{IM}.$

D. $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}.$

Câu 15: Cho hai tập hợp A = {1; 2; 3; 4; 5} và B = {1; 3; 5; 7}. Số phần tử của tập hợp A\B là

A. 2;

B. 3;

C. 1;

D. 6.

Câu 16: Cho hai tập hợp A = [– 2; 3), B = [1; 5]. Khi đó A $\cap$ B là tập hợp nào dưới đây ?

A. [– 2; 3);

B. [1; 3);

C. [1; 3];

D. (– 2; 5).

Câu 17: Hàm số f(x) = x² đồng biến trên khoảng nào dưới đây ?

A. (0; +∞);

B. (– 4; +∞);

C. (– ∞; 0);

D. (– ∞; – 1).

Câu 18: Cho hình chữ nhật ABCD có AB = 3a, BC = 4a. Độ dài của vectơ $\overrightarrow{AB}+\overrightarrow{AD}$ bằng

A. 25a;

B. 7a;

C. 5a;

D. a.

Câu 19: Cặp số nào sau đây là nghiệm của bất phương trình – 3x + 5y ≤ 6.

A. (2; 8);

B. (– 10; – 3);

C. (3; 3);

D. (0; 2).

Câu 20: Cặp số nào sau đây không là nghiệm của hệ bất phương trình -3x+5y$\le$6

A. (0; 0);

B. (1; 1);

C. (– 1; 1);

D. (– 1; – 1).

Câu 21: Cho 0° < α < 180°. Chọn câu trả lời đúng.

A. cosα < 0.

B. sinα > 0.

C. tanα < 0.

D. cotα > 0.

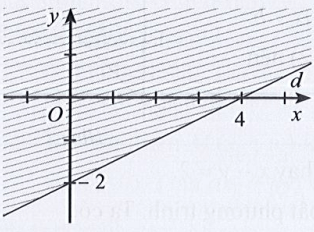
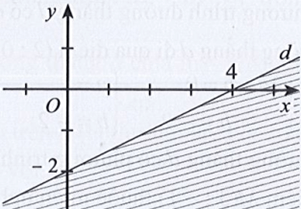
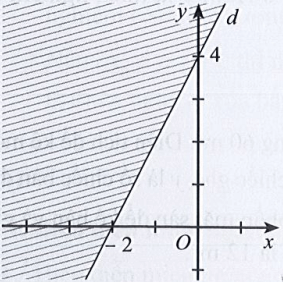
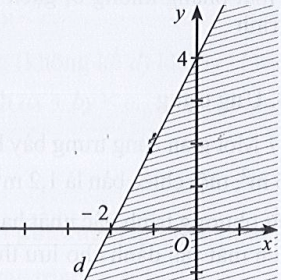
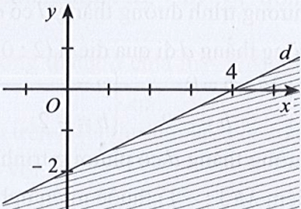
Câu 22: Miền nghiệm của bất phương trình x – 2y < 4 được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây?

A.

B.

C.

D.

Câu 23: Giá trị biểu thức T = sin²25° + sin²75° + sin²115° + sin²165° là:

A. T = sin 25°;

B. T = sin 75°;

C. T = 1;

D. T = 2.

Câu 24: Cho tam giác ABC có AB = 6,5 cm, AC = 8,5 cm, $\hat{A}$ =125° . Tính độ dài cạnh BC (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).

A. BC ≈ 177,9;

B. BC ≈ 13,3;

C. BC ≈ 51,1;

D. BC ≈ 7,1.

Câu 25: Miền nghiệm của bất phương trình 2x – 3y > 5 là nửa mặt phẳng (không kể đường thẳng d: 2x – 3y = 5) không chứa điểm có tọa độ nào sau đây?

A. (0; 0);

B. (3; 0);

C. (1; – 2);

D. (– 3; – 4).

II. PHẦN TỰ LUẬN

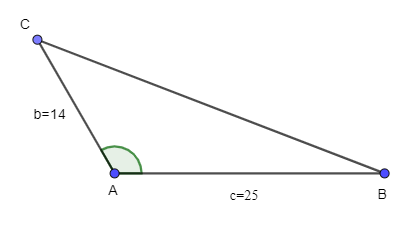
Câu 1: Giải tam giác ABC biết ABC có b = 14, c = 25 và $\hat{A}$ = 120°.

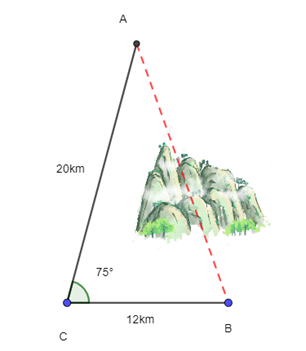
Câu 2: Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 20 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 12km. Góc tạo bởi dây AC và CB là 75°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.

Câu 3: Anh Trung có kế hoạch đầu tư 400 triệu đồng vào hai khoản X và Y. Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho khoản X. Viết hệ bất phương trình bậc nhất hai ẩn để mô tả hai khoản đầu tư đó và biểu diễn miền nghiệm của hệ bất phương trình vừa tìm được.

Lời giải

Gọi x (triệu đồng) là số tiền anh Trung đầu tư vào khoản X và y (triệu đồng) là số tiền anh Trung đầu tư vào khoản Y (x, y ≥ 0).

Vì anh Trung đầu tư 400 triệu đồng vào hai khoản X và Y nên ta có x + y ≤ 400.

Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng nên ta có x ≥ 100 và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho X nên ta cũng có y ≥ x hay x – y ≤ 0.

Từ đó ta có hệ bất phương trình sau: $\left\{\begin{array}{l}x+y\le 400\\ x\ge 100\\ x-y\le 0\end{array}\right.$.

Ta vẽ bốn đường thẳng:

d₁: x + y = 400 là đường thẳng đi qua hai điểm có tọa độ (400; 0) và (0; 400);

d₂: x = 100 là đường thẳng song song với trục Oy và đi qua điểm có tọa độ (100; 0);

d₃: x – y = 0 là đường thẳng đi qua hai điểm có tọa độ (0; 0) và (1; 1).

Ta xác định từng miền nghiệm của từng bất phương trình trong hệ, gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.

Miền nghiệm của hệ bất phương trình là miền trong tứ giác ABCD với như hình vẽ sau:

Câu 4: Lớp 10A có 36 học sinh, trong đó mỗi học sinh đều biết chơi ít nhất một trong hai môn thể thao đá cầu hoặc cầu lông. Biết rằng lớp 10A có 25 học sinh biết chơi đá cầu, có 20 học sinh biết chơi cầu lông. Hỏi lớp 10A có bao nhiêu học sinh biết chơi cả hai môn đá cầu và cầu lông?

-------------HẾT ----------

HƯỚNG DẪN GIẢI

I. PHẦN TRẮC NGHIỆM

1. A	2. B	3. C	4. C	5. A	6. A	7. B	8. A	9. C	10. D
11. A	12. C	13. C	14. A	15. B	16. B	17. D	18. C	19. C	20. C
21. B	22. B	23. D	24. B	25. B

Câu 1: Trong các câu dưới đây, câu nào là mệnh đề ?

A. Hà Nội là thủ đô của Việt Nam.

B. Hôm nay là thứ mấy ?

C. Mệt quá !

D. Mấy giờ rồi ?

Hướng dẫn giải

Đáp án đúng là: A

Ta có:

Câu “Hà Nội là thủ đô của Việt Nam” là câu khẳng định đúng. Do đó A là một mệnh đề.

Các câu “Hôm nay là thứ mấy?”, “Mấy giờ rồi?” là câu nghi vấn, không xác định được tính đúng sai. Do đó B và D không là mệnh đề.

Câu “Mệt quá!” là câu cảm thán không xác định được tính đúng sai. Do đó C không là mệnh đề.

Câu 2: Trong các mệnh đề dưới đây, mệnh đề nào đúng ?

A. 5 là số tự nhiên chẵn;

B. 5 là số nguyên tố;

C. 5 là số nguyên âm;

D. 5 là số chia hết cho 3.

Hướng dẫn giải

Đáp án đúng là: B

Ta có:

5 là số tự nhiên lẻ. Do đó A sai

5 có hai ước là 1 và chính nó nên 5 là số nguyên tố. Do đó B đúng.

5 là số nguyên dương. Do đó C sai.

5 chia 3 dư 2. Do đó D sai.

Câu 3: Cho tập hợp A = {1; 3; 5; 7; 9}. Số phần tử của tập hợp A là

A. 6;

B. 4;

C. 5;

D. 3.

Hướng dẫn giải

Đáp án đúng là: C

Tập hợp A có 5 phần tử.

Câu 4: Cho tập hợp B={x$\in$$R$$|a\le x<b$} Mệnh đề nào dưới đây đúng ?

A. B = [a; b];

B. B = (a; b];

C. B = [a; b) ;

D. B = (a; b).

Hướng dẫn giải

Đáp án đúng là: C

Ta có: B = {$-x\in R|a\le x<b$}.

Câu 5: Tập xác định của hàm số $f\left(x\right)=\sqrt{x-2}$ là

A. D = [2; +∞);

B. D = (2; +∞);

C. D = (– ∞; 2);

D. D = (– ∞; 2].

Hướng dẫn giải

Đáp án đúng là: A

Điều kiện xác định của hàm số f(x) là x – 2 ≥ 0 ⇔ x ≥ 2.

Vì vậy tập xác định của hàm số đã cho là D = [2; +∞).

Câu 6: Trong mặt phẳng Oxy, điểm nào dưới đây thuộc đồ thị của hàm số $y=\sqrt{x}$ ?

A. P(4; 2);

B. M(1; – 1);

C. N(2; 4);

D. Q(2; – 4).

Hướng dẫn giải

Đáp án đúng là: A

Thay tọa độ điểm P(4; 2) với x = 4 và y = 2 vào hàm số, ta được: 2=$\sqrt{4}$ là một mệnh đề đúng. Do đó P thuộc đồ thị hàm số đã cho.

Thay tọa độ điểm M(1; – 1) với x = 1 và y = – 1 vào hàm số, ta được: -1 = $\sqrt{1}$ là một mệnh đề sai. Do đó M không thuộc đồ thị hàm số đã cho.

Thay tọa độ điểm N(2; 4) với x = 2 và y = 4 vào hàm số, ta được: 4 = $\sqrt{2}$ là một mệnh đề sai. Do đó N không thuộc đồ thị hàm số đã cho.

Thay tọa độ điểm Q(2; – 4) với x = 2 và y = – 4 vào hàm số, ta được: -4 = $\sqrt{2}$ là một mệnh đề sai. Do đó Q không thuộc đồ thị hàm số đã cho.

Câu 7: Cho hàm số f(x) = x³ – 2. Giá trị f(1) bằng bao nhiêu?

A. 3;

B. – 1;

C. 2;

D. 1.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: f(1) = 1³ – 2 = – 1.

Câu 8: Hàm số nào dưới đây có đồ thị là đường thẳng như trong hình bên ?

A. y = x + 1;

B. y = x – 1;

C. y = – x + 1;

D. y = – x – 1.

Hướng dẫn giải

Đáp án đúng là: A

Vì đồ thị hàm số là đường thẳng nên là hàm số bậc nhất và có dạng y = ax + b (a ≠ 0).

Theo quan sát, ta thấy hàm số đi qua hai điểm có tọa độ (0 ; 1) và (– 1; 0) ta có hệ phương trình:

$\left\{\begin{array}{l}-a+b=0\\ b=1\end{array}\right.\iff \left\{\begin{array}{l}a=1\\ b=1\end{array}\right.$

Vì vậy hàm số cần tìm là y = x + 1.

Câu 9: Trong các mệnh đề dưới đây, mệnh đề nào đúng ?

A. Hàm số y = x là hàm số nghịch biến trên ℝ.

B. Đồ thị hàm số y = x là một đường cong.

C. Hàm số y = x là hàm số đồng biến trên ℝ.

D. Hàm số y = x là hàm hằng.

Hướng dẫn giải

Đáp án đúng là: C

Hàm số y = x là đường thẳng và có a = 1 > 0 nên hàm số đồng biến trên ℝ. Do đó C đúng.

Câu 10: Trong mặt phẳng Oxy, biết điểm M(2; y₀) thuộc đồ thị của hàm số y = 2x – 3. Giá trị của y₀ bằng:

A. 2;

B. 0;

C. – 1;

D. 1.

Hướng dẫn giải

Đáp án đúng là: D

Thay tọa độ điểm M với x = 2 và y = y₀ vào hàm số y = 2x – 3, ta được:

y₀ = 2.2 – 3 = 1.

Vậy y₀ = 1.

Câu 11: Trong mặt phẳng Oxy đồ thị của hàm số y = x² – 2x + 3 có trục đối xứng là đường thẳng nào dưới đây ?

A. x = 1;

B. x = – 1;

C. x = 2;

D. x = – 2.

Hướng dẫn giải

Đáp án đúng là: A

Đồ thị hàm số y = x² – 2x + 3 là hàm số bậc hai có trục đối xứng là x = $-\frac{b}{2a}$ = $-\frac{-2}{2.1}$ = 1.

Câu 12: Cho các vectơ $\overrightarrow{u},\overrightarrow{v},\overrightarrow{x},\overrightarrow{y}$ như trong hình:

Mệnh đề nào dưới đây là đúng?

A. Hai vectơ $\overrightarrow{x}$ và $\overrightarrow{y}$ cùng hướng;

B. Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ cùng hướng;

C. Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ ngược hướng;

D. Hai vectơ $\overrightarrow{x}$ và $\overrightarrow{y}$ ngược hướng.

Hướng dẫn giải

Đáp án đúng là: C

Từ hình vẽ, ta có:

Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ có giá là hai đường thẳng song song nên $\overrightarrow{u}$ và $\overrightarrow{v}$ cùng phương. Vectơ $\overrightarrow{u}$ có hướng từ trái sáng phải còn vectơ $\overrightarrow{v}$ có hướng từ phải sang trái. Do đó hai vectơ này ngược hướng.

Hai vectơ $\overrightarrow{x}$ và $\overrightarrow{y}$ có giá là hai đường thẳng không song song nên $\overrightarrow{x}$ và $\overrightarrow{y}$ không cùng phương. Do đó hai vectơ này không cùng hướng cũng không ngược hướng.

Câu 13: Vectơ có điểm đầu là A và điểm cuối là B được kí hiệu là:

A. AB;

B. BA;

C. $\overrightarrow{AB}$;

D. $\overrightarrow{BA}$;

Hướng dẫn giải

Đáp án đúng là: C

Vectơ có điểm đầu là A và điểm cuối là B được kí hiệu là: $\overrightarrow{AB}$.

Câu 14: Trong các bất phương trình đã cho sau đây. Bất phương trình nào là bất phương trình bậc nhất hai ẩn?

A. $\frac{1}{2}x$ – y ≥ 0;

B. -$\frac{3}{x}$ + y < – 9;

C. 9x² – 5y > – 87;

D. x² + y² ≥ 0.

Hướng dẫn giải

Đáp án đúng là: A

Ta có:

$\frac{1}{2}x$ – y ≥ 0 là bất phương trình bậc nhất hai ẩn x và y. Do đó A đúng.

$\frac{3}{x}$ + y < – 9 không có dạng bất phương trình bậc nhất hai ẩn. Do đó B sai.

9x² – 5y > – 87 là bất phương trình có bậc của biến x là bậc 2. Do đó C sai.

x² + y² ≥ 0 là bất phương trình có bậc của biến x và y là bậc 2. Do đó D sai.

Câu 15: Cho hai tập hợp A = {1; 2; 3; 4; 5} và B = {1; 3; 5; 7}. Số phần tử của tập hợp A\B là

A. 1;

B. 2;

C. 3;

D. 6.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: A\B = {2; 4}.

Do đó tập hợp này có 2 phần tử.

Câu 16: Cho hai tập hợp A = [– 2; 3), B = [1; 5]. Khi đó A $\cap$ B là tập hợp nào dưới đây ?

A. [– 2; 3);

B. [1; 3);

C. [1; 3];

D. (– 2; 5).

Hướng dẫn giải

Đáp án đúng là: B

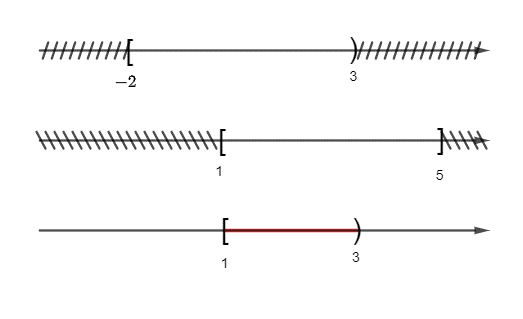
Ta có hình vẽ sau:

Khi đó A $\cap$ B = [1; 3).

Câu 17: Hàm số f(x) = x² đồng biến trên khoảng nào dưới đây ?

A. (– ∞; – 1);

B. (– 4; +∞);

C. (– ∞; 0);

D. (0; +∞).

Hướng dẫn giải

Đáp án đúng là: D

Xét hàm số bậc hai y = x² có:

Tọa độ điểm đỉnh là x = $-\frac{b}{2a}=-\frac{0}{2.1}=0\Rightarrow y=0$.

Ta có a = 1 > 0, khi đó:

Hàm số đồng biến trên (0; +∞);

Hàm số nghịch biến trên (– ∞; 0).

Câu 18: Cho hình chữ nhật ABCD có AB = 3a, BC = 4a. Độ dài của vectơ $\overrightarrow{AB}+\overrightarrow{AD}$ bằng

A. 25a;

B. 7a;

C. 5a;

D. a.

Hướng dẫn giải

Đáp án đúng là: C

Xét tam giác ABC vuông tại B, ta có:

AC² = AB² + BC² = (3a)² + (4a)² = 25a² (định lí Py – ta – go)

⇒ AC = 5a.

Vì ABCD là hình chữ nhật nên ABCD là hình bình hành. Do đó: $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$

⇒ $\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC=5a$.

Câu 19: Cặp số nào sau đây là nghiệm của bất phương trình – 3x + 5y ≤ 6.

A. (2; 8);

B. (– 10; – 3);

C. (3; 3);

D. (0; 2).

Hướng dẫn giải

Đáp án đúng là C

+) Thay x = 2, y = 8 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.2 + 5.8 ≤ 6 ⇔ 34 ≤ 6 (vô lí)

Do đó cặp số (2; 8) không là nghiệm của bất phương trình đã cho.

+) Thay x = – 10, y = – 3 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.(–10) + 5.(–3) ≤ 6 ⇔ 15 ≤ 6 (vô lí)

Do đó cặp số (– 10; – 3) không là nghiệm của bất phương trình đã cho.

+) Thay x = 3, y = 3 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.3 + 5.3 ≤ 6 ⇔ 6 ≤ 6 (luôn đúng)

Do đó cặp số (3; 3) không là nghiệm của bất phương trình đã cho.

+) Thay x = 0, y = 2 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.0 + 5.2 ≤ 6 ⇔ 10 ≤ 6 (vô lí)

Do đó cặp số (0; 2) không là nghiệm của bất phương trình đã cho.

Câu 20: Cặp số nào sau đây không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x+y\le 2\\ 2x-3y>-2\end{array}\right.$.

A. (0; 0);

B. (1; 1);

C. (– 1; 1);

D. (– 1; – 1).

Hướng dẫn giải

Đáp án đúng là C

Xét hệ phương trình: $\left\{\begin{array}{l}x+y\le 2\left(1\right)\\ 2x-3y>-2\left(2\right)\end{array}\right.$.

+) Thay x = 0 và y = 0 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:

(1) ⇔ 0 + 0 ≤ 2 ⇔ 0 ≤ 2 (luôn đúng);

(2) ⇔ 2.0 – 3.0 > – 2 ⇔ 0 > – 2 (luôn đúng).

Do đó cặp số (0; 0) là nghiệm của hệ bất phương trình đã cho.

+) Thay x = 1 và y = 1 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:

(1) ⇔ 1 + 1 ≤ 2 ⇔ 2 ≤ 2 (luôn đúng);

(2) ⇔ 2.1 – 3.1 > – 2 ⇔ – 1 > – 2 (luôn đúng).

Do đó cặp số (1; 1) là nghiệm của hệ bất phương trình đã cho.

+) Thay x = – 1 và y = 1 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:

(1) ⇔ – 1 + 1 ≤ 2 ⇔ 0 ≤ 2 (luôn đúng);

(2) ⇔ 2.(– 1) – 3.1 > – 2 ⇔ – 5 > – 2 (vô lí).

Do đó cặp số (– 1; 1) không là nghiệm của hệ bất phương trình đã cho.

+) Thay x = – 1 và y = – 1 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:

(1) ⇔ – 1 + (– 1) ≤ 2 ⇔ – 2 ≤ 2 (luôn đúng);

(2) ⇔ 2.(– 1) – 3.(– 1) > – 2 ⇔ 1 > – 2 (luôn đúng).

Do đó cặp số (– 1; – 1) là nghiệm của hệ bất phương trình đã cho.

Vậy cặp số (– 1; 1) không là nghiệm của hệ bất phương trình đã cho.

Câu 21: Cho 0° < α < 180°. Chọn câu trả lời đúng.

A. cosα < 0.

B. sinα > 0.

C. tanα < 0.

D. cotα > 0.

Hướng dẫn giải

Đáp án đúng là B

Với 0° < α < 180°, ta có:

– 1 < cosα < 1. Suy ra A sai.

0 < sinα < 1. Suy ra B đúng.

Do đó C và D sai.

Câu 22: Miền nghiệm của bất phương trình x – 2y < 4 được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây?

A.

B.

C.

D.

Hướng dẫn giải

Đáp án đúng là B

Phương trình đường thẳng d có dạng: x – 2y = 4.

Đường thẳng d cắt hai trục tọa độ Ox, Oy lần lượt tại hai điểm có tọa độ (4; 0) và (0; – 2).

Ta có: 0 – 2.0 = 0 < 4 (luôn đúng). Do đó miền nghiệm của bất phương trình chứa điểm (0; 0) và không chứa đường thẳng d.

Khi đó miền nghiệm là nửa mặt phẳng không bị gạch và không kể d được thể hiện trong hình vẽ sau:

Câu 23: Giá trị biểu thức T = sin²25° + sin²75° + sin²115° + sin²165° là:

A. T = sin 25°;

B. T = sin 75°;

C. T = 1;

D. T = 2.

Hướng dẫn giải

Đáp án đúng là D

T = sin²25° + sin²75° + sin²115° + sin²165°

= sin²25° + sin²75° + sin²75° + sin²25°

= 2sin²25° + 2sin²75°

= 2sin²25° + 2cos²25°

= 2(sin²25° + cos²25°)

= 2.1 = 2.

Câu 24: Cho tam giác ABC có AB = 6,5 cm, AC = 8,5 cm, $\hat{A}$ = 125°. Tính độ dài cạnh BC (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).

A. BC ≈ 177,9;

B. BC ≈ 13,3;

C. BC ≈ 51,1;

D. BC ≈ 7,1.

Hướng dẫn giải

Đáp án đúng là: B

Xét tam giác ABC, có:

BC² = AB² + AC² – 2.AB.AC.cosA

⇔ BC² = 6,5² + 8,5² – 2.6,5.8,5.cos125°

⇔ BC² ≈ 177,9

⇔ BC ≈ 13,3.

Vậy BC ≈ 13,3.

Câu 25: Miền nghiệm của bất phương trình 2x – 3y > 5 là nửa mặt phẳng (không kể đường thẳng d: 2x – 3y = 5) không chứa điểm có tọa độ nào sau đây?

A. (0; 0);

B. (3; 0);

C. (1; – 2);

D. (– 3; – 4).

Hướng dẫn giải

Đáp án đúng là B

+) Thay x = 0, y = 0 vào bất phương trình 2x – 3y > 5, ta được:

2.0 – 3.0 > 5 ⇔ 0 > 5 (vô lí)

Do đó cặp số (0; 0) không thuộc miền nghiệm của bất phương trình đã cho.

+) Thay x = 3, y = 0 vào bất phương trình 2x – 3y > 5, ta được:

2.3 – 3.0 > 5 ⇔ 6 > 5 (thỏa mãn)

Do đó cặp số (0; 0) thuộc miền nghiệm của bất phương trình đã cho.

+) Thay x = 1, y = – 2 vào bất phương trình 2x – 3y > 5, ta được:

2.1 – 3.(– 2) > 5 ⇔ 8 > 5 (thỏa mãn)

Do đó cặp số (1; – 2) thuộc miền nghiệm của bất phương trình đã cho.

+) Thay x = – 3, y = –4 vào bất phương trình 2x – 3y > 5, ta được:

2.(– 3) – 3.(– 4) > 5 ⇔ 6 > 5 (thỏa mãn)

Do đó cặp số (– 3; – 4) thuộc miền nghiệm của bất phương trình đã cho.

II. PHẦN TỰ LUẬN

Câu 1: Giải tam giác ABC biết ABC có b = 14, c = 25 và $\widehat{A}$ = 120°.

Lời giải

Xét ∆ABC, có:

Áp dụng định lí cosin, ta có:

BC² = AB² + AC² – 2AB.AC.cosA

⇔ BC² = 25² + 14² – 2.25.14.cos120°

⇔ BC² = 1 171

⇔ BC ≈ 34,22.

Áp dụng hệ quả của định lí cosin, ta có:

cosB = $\frac{a^2+c^2-b^2}{2.a.c}\approx \frac{34,{22}^2+{25}^2-{14}^2}{2.34,22.25}\approx 0,94$ ⇒ $\hat{B}\approx$20°45'.

Ta có: $\hat{C}=180°-\hat{A}-\hat{B}\approx 180°-120°-20°45\text{'}=39°15\text{'}$.

Câu 2: Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 20 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 12km. Góc tạo bởi dây AC và CB là 75°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.

Lời giải

Xét tam giác ABC, có:

Áp dụng định lí cosin trong tam giác ABC, có:

AB² = BC² + AC² – 2.AB.BC.cosA

⇔ AB² = 12² + 20² – 2.12.20.cos75°

⇔ AB² ≈ 419,77

⇔ AB ≈ 20,49 (km).

Ta có: AC + BC = 20 + 12 = 32 (km).

Vậy chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B là 32 – 20,49 ≈ 11,51 km.

Câu 3: Anh Trung có kế hoạch đầu tư 400 triệu đồng vào hai khoản X và Y. Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho khoản X. Viết hệ bất phương trình bậc nhất hai ẩn để mô tả hai khoản đầu tư đó và biểu diễn miền nghiệm của hệ bất phương trình vừa tìm được.

Lời giải

Gọi x (triệu đồng) là số tiền anh Trung đầu tư vào khoản X và y (triệu đồng) là số tiền anh Trung đầu tư vào khoản Y (x, y ≥ 0).

Vì anh Trung đầu tư 400 triệu đồng vào hai khoản X và Y nên ta có x + y ≤ 400.

Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng nên ta có x ≥ 100 và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho X nên ta cũng có y ≥ x hay x – y ≤ 0.

Từ đó ta có hệ bất phương trình sau: $\left\{\begin{array}{l}x+y\le 400\\ x\ge 100\\ x-y\le 0\end{array}\right.$.

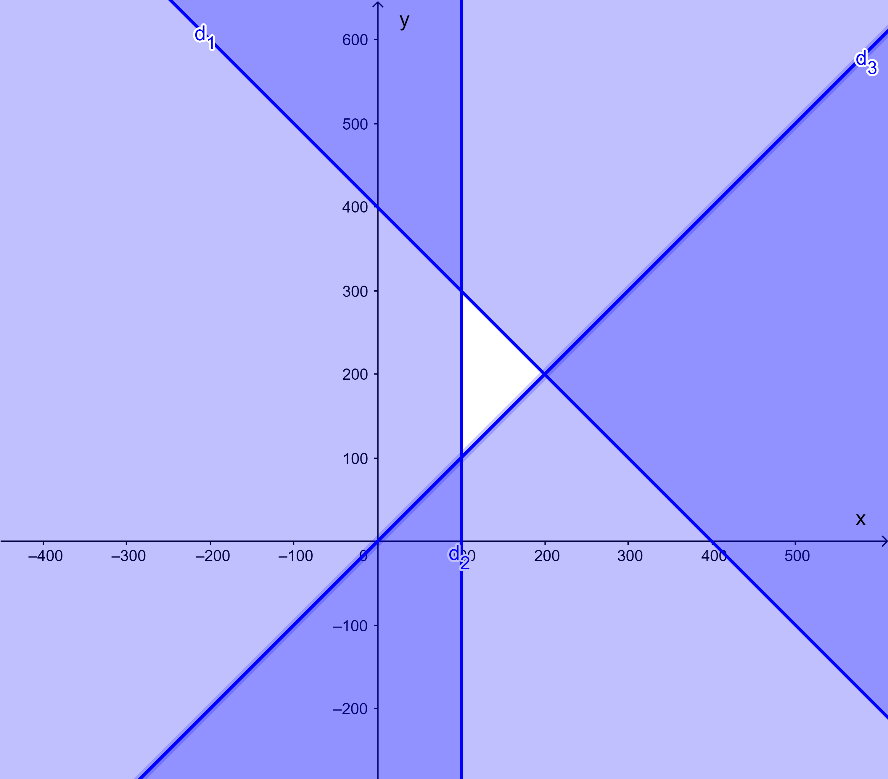
Ta vẽ bốn đường thẳng:

d₁: x + y = 400 là đường thẳng đi qua hai điểm có tọa độ (400; 0) và (0; 400);

d₂: x = 100 là đường thẳng song song với trục Oy và đi qua điểm có tọa độ (100; 0);

d₃: x – y = 0 là đường thẳng đi qua hai điểm có tọa độ (0; 0) và (1; 1).

Ta xác định từng miền nghiệm của từng bất phương trình trong hệ, gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.

Miền nghiệm của hệ bất phương trình là miền trong tứ giác ABCD với như hình vẽ sau:

Câu 4: Lớp 10A có 36 học sinh, trong đó mỗi học sinh đều biết chơi ít nhất một trong hai môn thể thao đá cầu hoặc cầu lông. Biết rằng lớp 10A có 25 học sinh biết chơi đá cầu, có 20 học sinh biết chơi cầu lông. Hỏi lớp 10A có bao nhiêu học sinh biết chơi cả hai môn đá cầu và cầu lông?

Lời giải

Gọi A là tập hợp số học sinh biết chơi đá cầu. Khi đó |A| = 25;

B là tập hợp số học sinh biết chơi cầu lông. Khi đó |B| = 20.

Vì mỗi học sinh đều biết chơi ít nhất một trong hai môn thể thao đá cầu hoặc cầu lông nên ta có: A ∪ B là tập hợp số học sinh của lớp 10A. Khi đó |A ∪ B| = 36.

Ta có: |A ∪ B| = |A| + |B| – |A ∩ B| ⇒ |A ∩ B| = 25 + 20 – 36 = 9 (học sinh).

Vậy lớp 10A có 9 học sinh biết chơi cả hai môn đá cầu và cầu lông.

MA TRẬN ĐỀ KIỂM TRA GIỮA KỲ 1

TT	Nội dung kiến thức	Đơn vị kiến thức	Mức độ nhận thức								Tổng			% tổng điểm
			Nhận biết		Thông hiểu		Vận dụng		Vận dụng cao		Số CH		TG (p)
			Số CH	TG (p)	Số CH	TG (p)	Số CH	TG (P)	Số CH	TG (p)	TN	TL
1	1. Mệnh đề toán học. Tập hợp	1.1. Mệnh đề	2	2	1	2		15		16	3	0	55	62
		1.2. Tập hợp	3	5	1	3	1		1		5	1
2	2. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn	2.1. Bất phương trình bậc nhất hai ẩn	1	1	1	2	1				3	0
		2.2. Hệ bất phương trình bậc nhất hai ẩn			1	3	1		1		2	1
3	3. Hàm số và đồ thị	3.1. Hàm số và đồ thị	1	1							1	0
		3.2. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng	1	2	1	3					2	0
4	3. Hệ thức lượng trong tam giác. Vectơ	3.1. Giá trị lượng giác của một góc từ 0° đến 180°	2	3	1	2	1	15			4	0	35	38
		3.2. Định lí côsin và định lí sin					1				0	1
		3.3. Giải tam giác và tính diện tích tam giác			1	3			1	8	1	1
		3.4. Khái niệm vectơ	2	2							2	0
		3.5. Tổng và hiệu của hai vectơ			1	2	1				2	0
Tổng			12	16	8	20	3	30	2	24	25	4	90
														100

Lưu ý:

- Các câu hỏi ở cấp độ nhận biết và thông hiểu là các câu hỏi trắc nghiệm khách quan 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.

- Các câu hỏi ở cấp độ vận dụng và vận dụng cao là các câu hỏi tự luận.

- Số điểm tính cho 1 câu trắc nghiệm là 0,20 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.

- Trong nội dung kiến thức:

+ Chỉ được chọn một câu mức độ vận dụng ở một trong ba nội dung 3.1; 3.2; 3.3.

+ (1*): chỉ được chọn một câu mức độ vận dụng ở một trong bốn nội dung 1.2; 2.1; 2.2; 2.3.

+ (1**): chỉ được chọn một câu mức độ vận dụng cao ở một trong hai nội dung 2.1; 2.3.

Xem thử