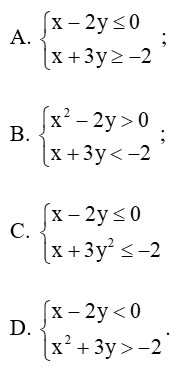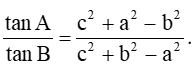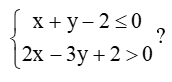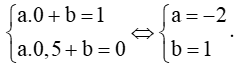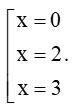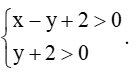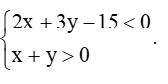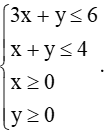Top 150 Đề thi Toán 10 Kết nối tri thức có đáp án

---

Haylamdo biên soạn và sưu tầm 100 Đề thi Toán lớp 10 Kết nối tri thức năm học 2023 mới nhất đầy đủ Học kì 1 và Học kì 2 gồm đề thi giữa kì, đề thi học kì có đáp án chi tiết, cực sát đề thi chính thức giúp học sinh ôn luyện & đạt điểm cao trong các bài thi Toán 10.

Mục lục Đề thi Toán lớp 10 Kết nối tri thức năm 2023 mới nhất

Xem thử

Chỉ 200k mua trọn bộ Đề thi Toán 10 Kết nối tri thức (cả năm) bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

- Đề thi Toán 10 Giữa kì 1 Kết nối tri thức

• Đề thi Giữa kì 1 Toán lớp 10 Kết nối tri thức có đáp án (4 đề)

  Xem đề thi

- Đề thi Toán 10 Học kì 1 Kết nối tri thức

• Đề thi Học kì 1 Toán lớp 10 Kết nối tri thức có đáp án (4 đề)

  Xem đề thi

- Đề thi Toán 10 Giữa kì 2 Kết nối tri thức

• Đề thi Giữa kì 2 Toán 10 Kết nối tri thức có đáp án (4 đề)

  Xem đề thi

- Đề thi Toán lớp 10 Học kì 2

• Đề thi Học kì 2 Toán lớp 10 Kết nối tri thức có đáp án (2 đề)

  Xem đề thi

Xem thêm đề thi Toán 10 cả ba sách:

• Top 20 Đề thi Giữa kì 1 Toán lớp 10 năm học 2023 có đáp án (cả ba sách)

  Xem đề thi

• Top 20 Đề thi Học kì 1 Toán 10 năm học 2023 có đáp án (cả ba sách)

  Xem đề thi

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Năm học 2023

Môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 1)

I. Trắc nghiệm (7 điểm)

Câu 1. Trong các câu sau, câu nào không phải mệnh đề?

A.8 là số chính phương;

B.2 là số chẵn;

C.Buồn ngủ quá!

D. Hình thoi có hai đường chéo vuông góc với nhau.

Câu 2. Tam giác ABC có bán kính đường tròn ngoại tiếp bằng R. Tìm mệnh đề sai trong các mệnh đề sau?

A. $\frac{a}{\sin A}=2R$;

B. $b=\frac{a.\sin B}{\sin A}$;

C. c = 2Rsin(A + B);

D. b = RsinA

Câu 3. Cho tập A = {0; 1}. Tập A có bao nhiêu tập con?

A. 3;

B. 6;

C. 4;

D. 2.

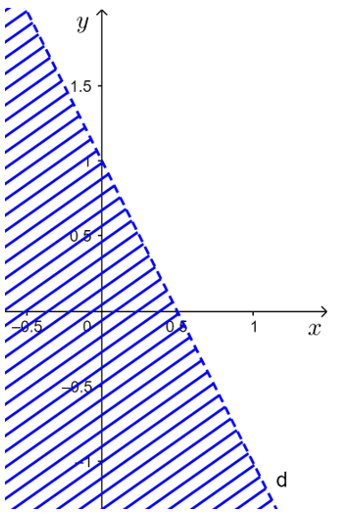
Câu 4. Điểm A(– 1; 3) là điểm thuộc miền nghiệm của bất phương trình:

A. – 3x + 2y – 4 > 0;

B. x + 3y < 0;

C. 3x – y > 0;

D. 2x – y + 4 > 0.

Câu 5. Với giá trị nào của x mệnh đề chứa biến P(x): 2x² – 1 < 0 là mệnh đề đúng:

A. 1;

B. 5;

C. 0;

D. $\frac{4}{5}$.

Câu 6. Cho α và β là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?

A. sin α = sin β;

B. cos α = – cos β;

C. tan α = – tan β;

D. cot α = cot β.

Câu 7. Hệ nào dưới đây là hệ bất phương trình bậc nhất hai ẩn?

Câu 8. Giá trị của sin 60° + cos 30° bằng bao nhiêu?

A. $\frac{\sqrt{3}}{2}$ ;

B. $\sqrt{3}$;

C. $\frac{\sqrt{3}}{3}$;

D. 1.

Câu9. Cho tập hợp A = [3; 7). Hãy chọn đáp án đúng.

A. A = {x ∈ ℝ | 3 < x ≤ 7};

B. A = {x ∈ ℝ | 3 ≤ x < 7};

C. A = {x ∈ ℝ | 3 < x < 7};

D. A = {x ∈ ℝ | 3 ≤ x ≤ 7}.

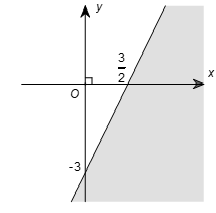
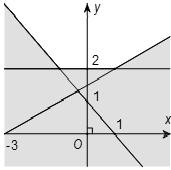
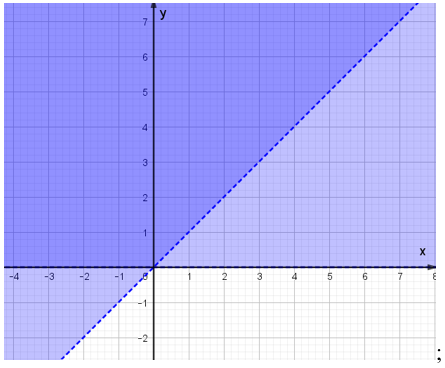
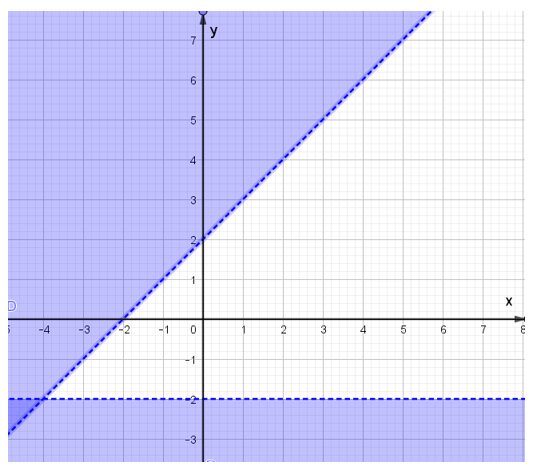
Câu 10. Phần tô đậm trong hình vẽ sau, biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?

A. 2x – y < 3;

B. 2x – y > 3;

C. x – 2y < 3;

D. x – 2y > 3.

Câu 11. Cho tam giác ABC thoả mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng ?

A. cos B + cos C = 2cos A;

B. sin B + sin C = 2sin A;

C. sin B + sin C = $\frac{1}{2}\sin A$;

D. sin B + cos C = 2sin A.

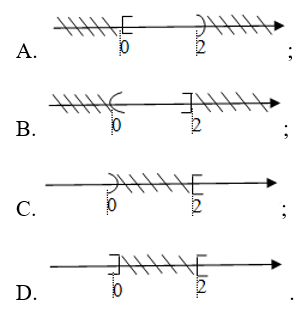
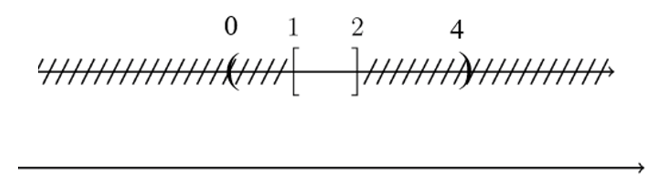
Câu 12. Cho A = [0; 5], B = (– ∞; 2). Biểu diễn trên trục số của tập hợp C_ℝ(A ∩ B) là hình nào?

Câu 13. Cho 0° < α < 180°, biết $\cos =-\frac{2}{3}$ . Tính tan α.

A. $\frac{5}{4}$ ;

B. $-\frac{5}{2}$ ;

C. $\frac{\sqrt{5}}{2}$ ;

D. $-\frac{\sqrt{5}}{2}$ .

Câu 14. Cho hệ bất phương trình . Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?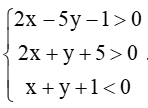

A. O(0; 0);

B. M(1; 0);

C. N(0; – 2);

D. P(0; 2).

Câu 15. Độ dài trung tuyến m_c ứng với cạnh c của DABC bằng biểu thức nào sau đây

A. $\frac{b^2+a^2}{2}-\frac{2}{4}$ ;

B. $\sqrt{\frac{b^2+a^2}{2}+\frac{c^2}{4}}$;

C. $\frac{1}{2}\sqrt{\left(2b^2+a^2\right)-c^2}$ ;

D. $\sqrt{\frac{b^2+a^2-c^2}{4}}$ .

Câu 16. Cho A là tập hợp các hình tứ giác; B là tập hợp các hình bình hành; C là tập hợp các hình thoi; D là tập hợp các hình vuông. Trong các khẳng định sau khẳng định nào sai?

(I) C ⊂ B ⊂ A;

(II) C ⊂ D ⊂ A;

(III) D ⊂ B ⊂ A.

A. (I);

B. (II);

C. (III);

D. (I) và (III).

Câu 17. Tam giác ABC có a = 16,8; $\hat{B}$= 56°13'; $\hat{C}$= 71°. Cạnh c bằng bao nhiêu?

A. 29,9;

B. 14,1;

C. 17,5;

D. 19,9.

Câu18. Phủ định của mệnh đề $"\exists x\in R:x^2<0"$ là

A. $\forall x\in R:x^2\le 0$;

B. $\exists x\in R:x^2\le 0$;

C. $\forall x\in R:x^2<0$;

D. $\forall x\in R:x^2\ge 0$.

Câu 19. Cho biết cot α = 5. Tính giá trị của E = 2 cos² α + 5 sin α cos α + 1?

A. $\frac{10}{26}$;

B. $\frac{100}{26}$;

C. $\frac{50}{26}$;

D. $\frac{101}{26}$.

Câu 20. Miền nghiệm của bất phương trình – x + 2 + 2(y – 2) < 2 (1 – x) là nửa mặt phẳng không chứa điểm nào trong các điểm sau?

A. (0; 0);

B. (1; 1);

C. (4; 2);

D. (1; – 1).

Câu 21. Mệnh đề nào sau đây sai?

A.$ℝ\backslash (-\infty ;3]=\left(3;+\infty \right)$ ;

B. $[-2;4)\cup [4;+\infty )=[-2;+\infty )$;

C. $[1;7]\cap \left(7;10\right)=\varnothing$;

D. $[1;5]\backslash \left(0;7)=[-1;0\right)$.

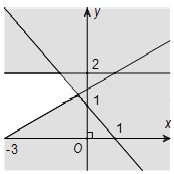
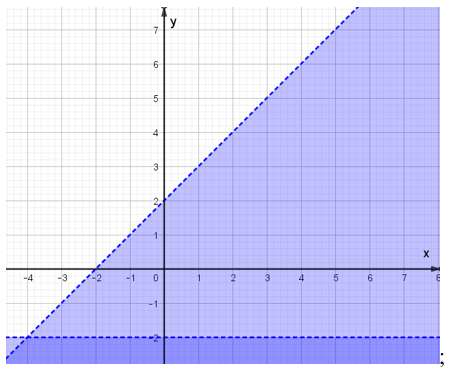
Câu 22. Miền nghiệm của hệ bất phương trình 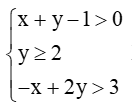là phần không tô đậm của hình vẽ nào trong các hình vẽ sau?

A.

B.

C.

D.

Câu 23. Cho tam giác ABC thoả mãn : b² + c² – a² = $\sqrt{3}$bc. Khi đó :

A. $\hat{A}$= 30°;

B. $\hat{A}$= 45°;

C. $\hat{A}$= 60°;

D. $\hat{A}$= 75°.

Câu24. Viết tập hợp A = {x | x ∈ ℕ, (x² – 5x + 6)(x – 1)(x + 3) = 0} bằng cách liệt kê các phần tử:

A. A = {1; 2; 3};

B. A = {– 1; 1; 2; 3};

C. A = {– 3; 1; 2; 3};

D. A = {– 3; – 1; 1; 2; 3}.

Câu 25. Trong các mệnh đề sau, mệnh đề nào sai?

A. Tam giác ABC là tam giác đều ⇔ Tam giác ABC cân;

B. Tam giác ABC là tam giác đều ⇔ Tam giác ABC có ba góc bằng nhau;

C. Tam giác ABC là tam giác đều ⇔ Tam giác ABC có ba cạnh bằng nhau;

D. Tam giác ABC là tam giác đều ⇔ Tam giác ABC cân và có một góc bằng 60°.

Câu 26. Một tam giác có ba cạnh là 26, 28, 30. Bán kính đường tròn nội tiếp là:

A. 16;

B. 8;

C. 4;

D. 4$\sqrt{2}$.

Câu 27. Bất phương trình nào dưới đây là bất phương trình bậc nhất hai ẩn?

A. 2x² + y – 3 < 0;

B. 5x + 3y² < 3;

C. 3²x + 9y ≤ 4²;

D. x² + xy – 4y < 5.

Câu 28. Trong các đẳng thức sau đây, đẳng thức nào sai?

A. sin 0° + cos 0° = 1;

B. sin 90° + cos 90° = 1;

C. sin 180° + cos 180° = – 1;

D. sin 60° + cos 60° = $\frac{\sqrt{3}+1}{2}$.

Câu 29. Cho mệnh đề: “Nếu a là số tự nhiên thì a là số hữu tỉ không âm”. Phát biểu mệnh đề đảo và xét tính đúng sai của mệnh đề này.

A. “Nếu a là số hữu tỉ không âm thì a là số tự nhiên”, đây là mệnh đề sai;

B. “Nếu a là số hữu tỉ không âm thì a là số tự nhiên”, đây là mệnh đề đúng;

C. “Nếu a là số tự nhiên không âm thì a là số hữu tỉ”, đây là mệnh đề sai;

D. “Nếu a là số hữu tỉ thì a là số tự nhiên không âm”, đây là mệnh đề đúng.

Câu 30. Cho hai góc nhọn α và β (α < β). Khẳng định nào sau đây là sai?

A. cos α < cos β;

B. sin α < sin β;

C. tan α + tan β > 0;

D. cot α > cot β;

Câu 31. Giá trị lớn nhất F_max của biểu thức F(x; y) = x + 2y trên miền xác định bởi hệ 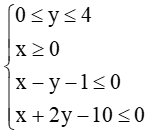là

A. F_max = 6;

B. F_max = 8;

C. F_max = 10;

D. F_max = 12.

Câu 32. Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 78°24'. Biết CA = 250 m, CB = 120 m. Khoảng cách AB bằng bao nhiêu ?

A. 266 m;

B. 255 m;

C. 166 m;

D. 298 m.

Câu 33. Cho bất phương trình x + y < 5. Khẳng định nào dưới đây đúng?

A. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + y = 5 chứa gốc tọa độ;

B. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + y = 5 không chứa gốc tọa độ;

C. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + y = – 5 chứa gốc tọa độ;

D. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + y = – 5 không chứa gốc tọa độ.

Câu 34. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Với mọi số thực x, nếu x < – 3 thì x² > 9;

B. Với mọi số thực x, nếu x² < 9 thì x < – 3;

C. Với mọi số thực x, nếu x < – 3 thì x² < 9;

D. Với mọi số thực x, nếu x² > 9 thì x > – 3.

Câu 35. Điểm nào dưới đây không thuộc miền nghiệm của bất phương trình 2x – 3y > 15?

A. (1; – 5);

B. (2; – 5);

C. (3; – 3);

D. (10; 1).

II. Tự luận (3 điểm)

Câu 1. Cho 2 tập hợp A = (– 1; 4), B = (m – 1; 2m + 1].

a) Khi m = 2, hãy tìm A ∪ B, A ∩ B.

b) Tìm tất cả các giá trị thực của tham số m để B ⊂ A.

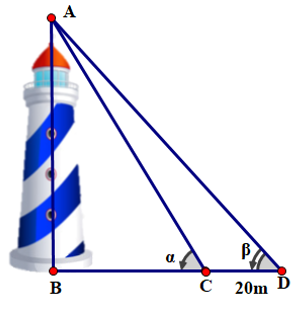
Câu 2. Để đo chiều cao của tháp có đỉnh A, chân tháp là B, người ta đứng dưới mặt đất quan sát ở hai điểm C và D sao cho B, C, D thẳng hàng (như hình vẽ).

Qua đo đạc, ta thu được DC = 20 m, α = 58°; β = 47°. Chiều cao của tháp gần nhất với kết quả nào dưới đây?

Câu 3. Cho tam giác ABC với BC = a, AC = b và AB = c. Chứng minh rằng:

-----HẾT-----

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Năm học 2023

Môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 2)

I. Trắc nghiệm (7 điểm)

Câu 1. Trong các phát biểu sau, phát biểu nào không phải là mệnh đề?

A. 2 là số nguyên âm;

B. Bạn có thích học môn Toán không?;

C. 13 là số nguyên tố;

D. Số 15 chia hết cho 2.

Câu 2. Trong các tập hợp sau, tập hợp nào là con của tập hợp A = {1; 2; 3; 4; 5}?

A. A₁ = {1; 6};

B. A₂ = {0; 1; 3};

C. A₃ = {4; 5};

D. A₄ = {0}.

Câu 3.Cho các tập hợp A = {x ∈ ℝ | – 5 ≤ x < 1} và B = {x ∈ ℝ | – 3 < x ≤ 3}. Tìm tập hợp A ∪ B.A. A ∪ B = [– 5; 1);

B. A ∪ B = [– 5; 3];

C. A ∪ B = (– 3; 1);

D. A ∪ B = (– 3; 3].

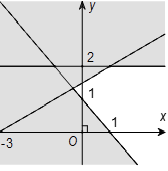
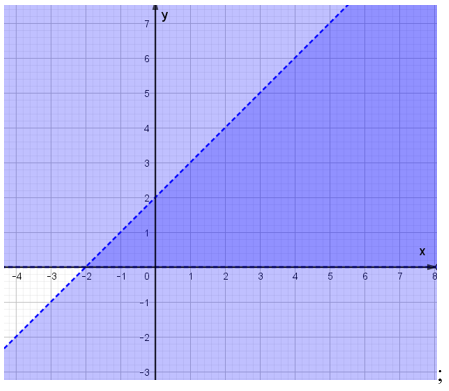
Câu 4.Nửa mặt phẳng không bị gạch chéo ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?

A. x + 2y > 1;

B. 2x + y > 1;

C. 2x + y < 1;

D. 2x – y > 1.

Câu 5. Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình:

A. (0; 0);

B. (1; 1);

C. (– 1; 1);

D. (– 1; – 1).

Câu 6.Mệnh đề nào sau đây đúng?

A. sin (180° – α) = – sin α;

B. cos (180° – α) = – cos α;

C. tan (180° – α) = tan α;

D. cot (180° – α) = cot α);

Câu 7. Tam giác ABC có BC = 1, AC = 3,$\hat{C}={60}^0$. Tính độ dài cạnh AB.

A. $\sqrt{13}$;

B. $\frac{\sqrt{46}}{2}$;

C. $\frac{\sqrt{34}}{2}$;

D. $\sqrt{7}$.

Câu 8. Cho hai mệnh đề P: “x là số chẵn” và Q: “x chia hết cho 2”.

Phát biểu mệnh đề P kéo theo Q.

A. Hoặc x là số chẵn hoặc x chia hết cho 2;

B. Nếu x là số chẵn thì x chia hết cho 2;

C. Nếu x chia hết cho 2 thì x là số chẵn;

D. x là số chẵn và x chia hết cho 2.

Câu 9. Trong các cặp số sau đây: (– 5; 0); (– 2; 1); (– 1; 3); (– 7; 0). Có bao nhiêu cặp số là nghiệm của bất phương trình x – 4y + 5 ≥ 0?

A. 0;

B. 1;

C. 3;

D. 4.

Câu 10. Giá trị của biểu thức P = sin30°.cos15° + sin150°.cos165° là

A. 0;

B. 1;

C. – 1;

D. 0,5.

Câu 11. Mệnh đề phủ định của mệnh đề P: “∃x, x² + 2x + 3 là số chính phương” là:

A. ∀x, x² + 2x + 3 không là số chính phương;

B. ∃x, x² + 2x + 3 là số nguyên tố;

C. ∀x, x² + 2x + 3 là hợp số;

D. ∃x, x² + 2x + 3 là số thực.

Câu 12. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn ?

A. 2x² + 1 ≥ y + 2x²;

B. 2x – 6y + 5 < 2x – 6y + 3;

C. 4x² < 2x + 5y – 6;

D. 2x³ + 1 ≥ y + 2x².

Câu 13. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Khẳng định nào dưới đây đúng?

A. a² = b² + c² + 2bcsinA;

B. a² = b² + c² – 2bccosA;

C. a² = b² + c² – 2acsinA;

D. a² = b² + c² + 2abcosA.

Câu 14. Cho tập hợp D = {x ∈ ℕ^* | x(x – 2)(x – 3) = 0}.

Viết lại tập hợp D dưới dạng liệt kê các phần tử của tập hợp đó.

A. D = {0; 1; 2};

B. D = {2; 3};

C. D = {0; 2; 3};

D. D = {1; 2}.

Câu 15. Hệ nào là hệ bất phương trình bậc nhất hai ẩn trong các hệ sau?

Câu 16. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. S là diện tích và p là nửa chu vi tam giác. R là bán kính đường tròn ngoại tiếp và r là bán kính đường tròn nội tiếp tam giác. Công thức nào sau đây sai?

A. S = $\frac{abc}{4R}$;

B. S = pr ;

C. S = $\sqrt{p(p+a)(p+b)(p+c)}$;

D. S = $\frac{1}{2}bc.\sin A$

Câu 17. Cho $\hat{A}={45}^0$, chọn đáp án SAI trong các đáp án dưới đây?

A. sin A = $\frac{\sqrt{3}}{2}$;

B. cos A = $\frac{\sqrt{2}}{2}$;

C. tan A = 1;

D. cot A = 1.

Câu 18. Cặp số nào sau đây là một nghiệm của bất phương trình: 3x + 2(y + 3) > 4(x + 1) – y + 3 ?

A. (–3; 0);

B. (3; 1);

C. (2; 1);

D. (0; 0).

Câu 19. Cho tập hợp B gồm các số tự nhiên bé hơn 20 và chia hết cho 4.

Viết tập hợp trên dưới dạng chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.

A. B = {x ∈ ℤ | x ≤ 20 và x ⁝ 4};

B. B = {x ∈ ℤ | x < 20 và x ⁝ 4};

C. B = {x ∈ ℕ | x ≤ 20 và x ⁝ 4};

D. B = {x ∈ ℕ | x < 20 và x ⁝ 4}.

Câu 20. Cho tam giác ABC biết $\frac{\sin B}{\sin C}=\sqrt{3}$ và AB = $2\sqrt{2}$. Tính AC.

A. $2\sqrt{2}$;

B. $2\sqrt{3}$;

C. $2\sqrt{6}$;

D. $2\sqrt{5}$.

Câu 21. Cho tập hợp K = [1 ; 7) \ (– 3 ; 5). Khẳng định nào sau đây đúng ?

A. K = [1; 7);

B. K = (– 3; 7);

C. K = [1; 5);

D. K = [5; 7).

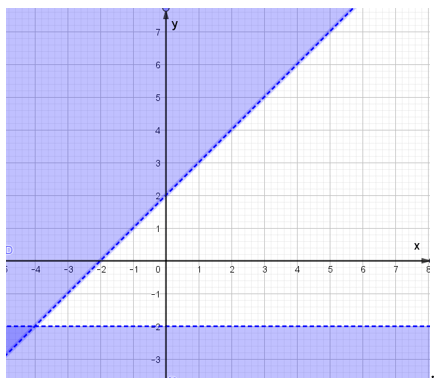
Câu 22. Miền nghiệm của hệ bất phương trình 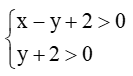là phần màu trắng được biểu diễn trong hình vẽ nào dưới dây ?

A.

B.

C.

D.

Câu 23. Cho hai nửa khoảng M = (0; 2], N = [1; 4). Tìm E = C_ℝ(M ∩ N).

A. E = (0; 4);

B. E = [1; 2];

C. E = (– ∞; 1) ∪ (2; +∞);

D. E = (– ∞; 0] ∪ [4; +∞).

Câu 24. Cho mệnh đề: “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được một đường tròn”.

Mệnh đề đảo của mệnh đề trên là:

A. “Tứ giác là một hình thoi khi và chỉ khi tứ giác đó nội tiếp được trong một đường tròn”;

B. “Một tứ giác nội tiếp được trong một đường tròn khi và chỉ khi tứ giác đó là hình thoi”;

C. “Nếu một tứ giác nội tiếp được trong một đường tròn thì tứ giác đó là hình thoi”;

D. “Tứ giác là một hình thoi kéo theo tứ giác đó nội tiếp được trong một đường tròn”.

Câu 25. Cho tam giác ABC có AB = 4, AC = 8 và $\hat{A}={30}^0$. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

A. 7;

B. 6;

C. 5;

D. 4.

Câu 26. Cho góc α thỏa mãn ${\cos }^2\alpha =\frac{1}{6}$. Khẳng định nào sau đây là đúng?

A. 1 + cot²α = 6;

B. 1 + cot²α = 5;

C. 1 + tan²α = 5;

D. 1 + tan²α = 6.

Câu 27. Cho định lý sau: “Nếu hai tam giác bằng nhau thì hai tam giác đó đồng dạng”.

Phát biểu định lý trên dưới dạng điều kiện cần.

A. Hai tam giác bằng nhau kéo theo hai tam giác đó đồng dạng;

B. Hai tam giác bằng nhau là điều kiện cần để hai tam giác đó đồng dạng;

C. Hai tam giác đồng dạng là điều kiện cần để hai tam giác đó bằng nhau;

D. Hai tam giác bằng nhau tương đương với hai tam giác đó đồng dạng.

Câu 28. Miền nghiệm của bất phương trình x – 3y + 3 > 0 là:

A. Nửa mặt phẳng bờ là đường thẳng Δ: x – 3y + 3 = 0, không chứa gốc tọa độ O;

B. Nửa mặt phẳng bờ là đường thẳng Δ: x – 3y + 3 = 0 (không kể bờ), không chứa gốc tọa độ O;

C. Nửa mặt phẳng bờ là đường thẳng Δ: x – 3y + 3 = 0, chứa gốc tọa độ O;

D. Nửa mặt phẳng bờ là đường thẳng Δ: x – 3y + 3 = 0 (không kể bờ), chứa gốc tọa độ O.

Câu 29. Cho các mệnh đề dưới đây:

(1) 24 là số nguyên tố.

(2) Phương trình x² – 5x + 9 = 0 có 2 nghiệm thực phân biệt.

(3) Phương trình x² + 1 = 0 có 2 nghiệm thực phân biệt.

(4) Mọi số nguyên lẻ đều không chia hết cho 2.

Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 1;

B. 2;

C. 3;

D. 4.

Câu 30. Bạn Vân có tối đa 120 phút để trồng rau trong vườn. Biết có hai loại rau là rau cải và rau muống, một cây rau cải trồng mất 5 phút, một cây rau muống trồng mất 7 phút. Gọi số cây rau cải bạn Vân trồng được là x cây, số cây rau muống bạn Vân trồng được là y cây. Các bất phương trình mô tả điều kiện của bài toán là:

A. 7x + 5y ≥ 120; x > 0; y > 0;

B. 5x + 7y ≤ 120; x ≥ 0; y ≥ 0;

C. 7x + 5y > 120; x > 0; y > 0;

D. 7x + 5y < 120; x < 0; y > 0.

Câu 31. Cho tam giác ABC. Xét dấu của biểu thức P = cos $\frac{A}{2}$. sin B?

A. P > 0;

B. P < 0;

C. P = 0;

D. Một kết quả khác.

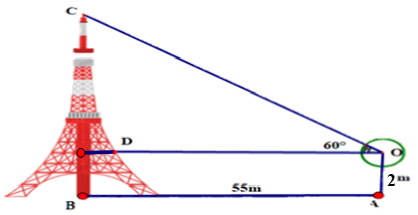
Câu 32. Để xác định chiều cao của một tòa tháp mà không cần lên đỉnh của tòa nhà người ta làm như sau: đặt giác kế thẳng đứng cách chân tháp một khoảng AB = 55 m, chiều cao của giác kế là OA = 2 m.

Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh C của tháp. Đọc trên giác kế số đo góc $\widehat{COD}={60}^0$.

Chiều cao của ngọn tháo gần nhất với giá trị nào sau đây?

A. 87 m;

B. 90 m;

C. 97 m;

D. 100 m.

Câu 33. Cho góc α với 0° < α < 180°. Tính giá trị của cosα, biết $\tan \alpha =-2\sqrt{2}$.

A. $\frac{1}{3}$;

B. $\frac{2\sqrt{2}}{3}$;

C. $\frac{1}{3}$;

D. $\frac{\sqrt{2}}{3}$.

Câu 34. Miền nghiệm của hệ bất phương trình 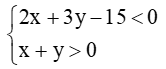chứa điểm nào trong các điểm sau đây ?

A. (1; 15);

B. (7; 8);

C. (9; 11);

D. (1; 2).

Câu 35. Cho tam giác ABC có AB = 5 , $\hat{A}={30}^0$, $\hat{B}={75}^0$. Tính diện tích tam giác ABC.

A. $\frac{5}{2}$;

B. 4;

C. $\frac{25}{4}$;

D. 5.

II. Tự luận (3 điểm)

Câu 1. Cho hai tập hợp A = (0; 3), B = (2; 4). Xác định các tập hợp A ∪ B, A ∩ B, A \ B và C_ℝA.

Câu 2. Một phân xưởng có hai máy đặc chủng loại 1 và loại 2 sản xuất hai loại sản phẩm kí hiệu là A và B. Một tấn sản phẩm loại A lãi 2 triệu đồng, một tấn sản phẩm loại B lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A phải dùng máy loại 1 trong 3 giờ và máy loại 2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B phải dùng máy loại 1 trong 1 giờ và máy loại 2 trong 1 giờ. Máy loại 1 làm việc không quá 6 giờ một ngày, máy loại 2 làm việc không quá 4 giờ 1 ngày. Hỏi cần sản xuất bao nhiêu tấn sản phẩm loại A và loại B để số tiền lãi mà phân xưởng này có thể thu được trong một ngày là lớn nhất?

Câu 3. Cho tam giác ABC. Chứng minh rằng:

sin A = sin B . cos C + sin C . cos B.

-----HẾT----

C. Đáp án và hướng dẫn giải đề kiểm tra giữa kỳ 1

ĐÁP ÁN ĐỀ SỐ 2

I. Bảng đáp án trắc nghiệm

1.B	2. C	3. B	4. B	5. C	6. B	7. D
8. B	9. B	10. A	11. A	12. A	13. B	14. B
15. C	16. C	17. A	18. A	19. D	20. C	21. D
22. D	23. C	24. C	25. C	26. D	27. C	28. D
29. A	30. B	31. A	32. C	33. A	34. D	35. C

II. Hướng dẫn giải chi tiết trắc nghiệm

Câu 1.

Đáp án đúng là: B

Phát biểu “Bạn có thích học môn Toán không?” là một câu hỏi, không khẳng định tính đúng sai nên đây không phải mệnh đề.

Câu 2.

Đáp án đúng là: C

Tập con của tập hợp A là tập hợp gồm các phần tử đều là phần tử của tập hợp A.

Tập A₁ = {1; 6} không là tập con của tập A vì 6 ∉ A.

Tập A₂ = {0; 1; 3} không là tập con của tập A vì 0 ∉ A.

Tập A₃ = {4; 5} là tập con của tập A vì 4 ∈ A, 5 ∈ A.

Tập A₄ = {0} không là tập con của tập A vì 0 ∉ A.

Vậy chỉ có tập A₃ là tập con của tập A.

Câu 3.

Đáp án đúng là: B

Ta có: A = {x ∈ ℝ | – 5 ≤ x < 1} = [– 5; 1)

Và B = {x ∈ ℝ | – 3 < x ≤ 3} = (– 3; 3].

Do đó, A ∪ B = {x | x ∈ A hoặc x ∈ B} = [– 5; 3].

Câu 4.

Đáp án đúng là: B

Giả sử đường thẳng d có phương trình: y = ax + b.

Từ hình vẽ ta thấy, đường thẳng d đi qua hai điểm có tọa độ (0; 1) và (0,5; 0).

Khi đó ta có hệ

Do đó, d: y = – 2x + 1 hay d: 2x + y = 1.

Lấy điểm O(0; 0) không thuộc đường thẳng d, ta thấy 2 . 0 + 0 = 0 < 1 và nửa mặt phẳng không bị gạch chéo không chứa điểm O.

Vậy nửa mặt phẳng không bị gạch chéo ở hình đã cho là miền nghiệm của bất phương trình 2x + y > 1.

Câu 5.

Đáp án đúng là: C

Thay lần lượt các cặp số vào hệ bất phương trình 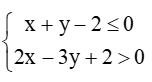ta thấy chỉ có cặp số (– 1; 1) không thỏa mãn, do cặp số này không thỏa mãn bất phương trình thứ hai của hệ (2 . (– 1) – 3 . 1 + 2 = – 3 < 0).

Vậy trong các cặp số đã cho, cặp số (– 1; 1) không là nghiệm của hệ bất phương trình đã cho.

Câu 6.

Đáp án đúng là: B

Hai góc bù nhau thì sin bằng nhau, côsin, tang và côtang đối nhau.

Do đó, sin (180° – α) = sin α; cos (180° – α) = – cos α;

tan (180° – α) = – tan α; cot (180° – α) = – cot α).

Vậy trong các đáp án đã cho, đáp án đúng là đáp án B.

Câu 7.

Đáp án đúng là: D

Áp dụng định lí côsin trong tam giác ABC ta có:

AB² = BC² + AC² – 2 BC. AC . cosC = 1² + 3² – 2 . 1 . 3 . cos 60° = 7.

Suy ra AB = $\sqrt{7}$.

Câu 8.

Đáp án đúng là: B

Vì mệnh đề kéo theo được phát biểu dưới dạng là “Nếu P thì Q”.

Nên mệnh đề P kéo theo Q là “Nếu x là số chẵn thì x chia hết cho 2”.

Câu 9.

Đáp án đúng là: B

Ta có:

– 5 – 4.0 + 5 = 0, vậy (– 5; 0) là nghiệm của bất phương trình.

– 2 – 4.1 + 5 = – 1 < 0, vậy (– 2; 1) không là nghiệm của bất phương trình.

– 1 – 4.3 + 5 = – 8 < 0, vậy (– 1; 3) không là nghiệm của bất phương trình.

– 7 – 4.0 + 5 = – 2 < 0, vậy (–7; 0) không là nghiệm của bất phương trình.

Vậy có 1 cặp số là nghiệm của bất phương trình.

Câu 10.

Đáp án đúng là: A

Sử dụng công thức: sin (180° – α) = sinα và cos(180° – α) = –cosα.

Ta có: sin30° = sin150°; cos15° = –cos165°

P = sin30°.cos15° + sin150°.cos165°= sin30°.cos15° – sin30°.cos15°=0.

Câu 11.

Đáp án đúng là: A

Ta có:

Phủ định của ∃ là ∀.

Phủ định của “là số chính phương” là “không là số chính phương”.

Vậy mệnh đề phủ định $\overline{)P}$ của mệnh đề P là: “∀x, x² + 2x + 3 không là số chính phương”.

Câu 12.

Đáp án đúng là: A

Xét bất phương trình 2x² + 1 ≥ y + 2x² ⇔ 2x² + 1 – 2x² – y ≥ 0 ⇔ 0x – y ≥ – 1 (1)

Bất phương trình (1) có hai ẩn x, y có lũy thừa bậc cao nhất là bậc một và các hệ số a = 0, b = –1, c = – 1.

Do đó, đây là một bất phương trình bậc nhất hai ẩn.

Chú ý: Đáp án B không thỏa mãn vì ta biến đổi đưa về được 5 < 3 (vô lí).

Đáp án C, D bậc của các ẩn không phải bậc nhất.

Câu 13.

Đáp án đúng là: B

Định lí côsin:

Trong tam giác ABC: a² = b² + c² – 2bccosA.

Vậy đáp án đúng là B.

Câu 14.

Đáp án đúng là: B

Ta có: x(x – 2)(x – 3) = 0 ⇔

Vì x ∈ ℕ^* nên ta loại nghiệm x = 0.

Do đó tập hợp D gồm 2 phần tử là 2 và 3.

Vậy D = {2; 3}.

Câu 15.

Đáp án đúng là: C

Xét hệ 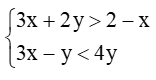ta có:

3x + 2y > 2 – x ⇔ 4x + 2y > 2 là một bất phương trình bậc nhất hai ẩn;

3x – y < 4y ⇔ 3x – 5y < 0 là một bất phương trình bậc nhất hai ẩn.

Do đó, 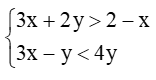là hệ bất phương trình bậc nhất hai ẩn.

Câu 16.

Đáp án đúng là: C

Các công thức tính diện tích tam giác ABC là:

S = $\frac{1}{2}$bcsinA = $\frac{abc}{4R}$ = pr = $\sqrt{p(p-a)(p-b)(p-c)}$.

Trong đó, S = $\sqrt{p(p-a)(p-b)(p-c)}$ là công thức Heron.

Do đó C sai.

Câu 17.

Đáp án đúng là: A

Ta có sin A = sin 45° = $\frac{\sqrt{2}}{2}$, suy ra đáp án sai là A.

cos A = cos 45° = $\frac{\sqrt{2}}{2}$;

tan A = tan 45° = 1;

cot A = cot 45° = 1.

Vậy các đáp án B, C, D đúng.

Câu 18.

Đáp án đúng là: A

Ta có:

3x + 2(y + 3) > 4(x + 1) – y + 3

⇔ 3x + 2y + 6 > 4x + 4 – y + 3

⇔ 3x + 2y + 6 – 4x – 4 + y – 3 > 0

⇔ –x + 3y – 1 > 0

Xét cặp số (x₀; y₀) = (–3; 0) và bất phương trình –x + 3y – 1 > 0 ta có:

–(–3) + 3.0 – 1 = 2 > 0

Do đó, cặp số (–3; 0) là một nghiệm của bất phương trình: 3x + 2(y + 3) > 4(x + 1) – y + 3.

Câu 19.

Đáp án đúng là: D

Gọi x là phần tử của tập hợp B, ta có:

+ Tập hợp B gồm các số tự nhiên nên x ∈ ℕ.

+ Tập hợp B gồm các số tự nhiên bé hơn 20 và chia hết cho 4 nên x < 20 và x ⁝ 4.

Do đó tập hợp B được viết dưới dạng chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó như sau:

B = {x ∈ ℕ | x < 20 và x ⁝ 4}.

Câu 20.

Đáp án đúng là: C

Áp dụng định lý sin trong tam giác ABC, ta có

$\frac{AC}{\sin B}=\frac{AB}{\sin C}\iff \frac{\sin B}{\sin C}=\frac{AC}{AB}$

Từ $\frac{\sin B}{\sin C}=\sqrt{3}$ suy ra $\frac{AC}{AB}=\sqrt{3}$

$\iff AC=AB\sqrt{3}=2\sqrt{2}.\sqrt{3}=2\sqrt{6}$.

Câu 21.

Đáp án đúng là: D

Tập hợp K là tập hợp các phần tử thuộc [1; 7) nhưng không thuộc (– 3; 5).

Ta xác định tập hợp K bằng cách vẽ trục số như sau: Trên cùng một trục số, tô đậm nửa khoảng [1; 7) và gạch bỏ khoảng (–3; 5), sau đó bỏ luôn các khoảng chưa được tô hoặc đánh dấu. Phần tô đậm không bị gạch bỏ chính là tập hợp K.

Vậy K = [1 ; 7) \ (– 3 ; 5) = [5 ; 7).

Câu 22.

Đáp án đúng là: D

+) Bất phương trình x – y + 2 > 0 có:

Điểm (0; 0) không nằm trên đường thẳng x – y + 2 = 0 và 0 – 0 + 2 = 2 > 0 nên miền nghiệm của bất phương trình x – y + 2 > 0 là nửa mặt phẳng bờ là đường thẳng x – y + 2 = 0 (không kể bờ) chứa điểm (0; 0).

+) Bất phương trình y + 2 > 0 có:

Điểm (0; 0) không nằm trên đường thẳng y + 2 = 0 và 0 + 2 = 2 > 0 nên miền nghiệm của bất phương trình y + 2 > 0 là nửa mặt phẳng bờ là đường thẳng y + 2 = 0 (không kể bờ) chứa điểm (0; 0).

Miền màu trắng trong hình vẽ là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình

Câu 23.

Đáp án đúng là: C

Ta biểu diễn hai nửa khoảng M = (0; 2], N = [1; 4) lên cùng một trục số. Phần không bị gạch chính là giao của hai tập hợp M và N.

Do đó, M ∩ N = (0; 2] ∩ [1; 4) = [1; 2].

Hiển nhiên, M ∩ N là một tập con của tập số thực ℝ.

Do đó, E = C_ℝ(M ∩ N) = ℝ \ (M ∩ N).

Ta có biểu diễn:

Tập hợp ℝ \ (M ∩ N) là tập hợp các phần tử thuộc ℝ nhưng không thuộc M ∩ N.

Vậy E = C_ℝ(M ∩ N) = ℝ \ (M ∩ N) = (– ∞; 1) ∪ (2; +∞).

Câu 24.

Đáp án đúng là: C

Xét mệnh đề “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được trong một đường tròn”, ta có:

P: “Tứ giác là một hình thoi”.

Q: “Tứ giác đó nội tiếp được một đường tròn”.

Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu một tứ giác nội tiếp được trong một đường tròn thì tứ giác đó là hình thoi”.

Đối chiếu với các đáp án, ta thấy mệnh đề ở câu C là phù hợp nhất.

Câu 25.

Đáp án đúng là: C

Tam giác ABC có: BC² = AB² + AC² - 2.AB.BC.cosA(định lí côsin)

Thay số: BC² = 4² + 8² - 2.4.8.cos30⁰ = 80 - $32\sqrt{3}$

Do đó: BC ≈ 5.

Ta có: $\frac{BC}{\sin A}=2R\left(\mathrm{định}\mathrm{lý}\sin \right)\Rightarrow \frac{BC}{2\sin A}\approx \frac{5}{2\sin {30}^o}=5$.

Câu 26.

Đáp án đúng là: D

Sử dụng cos²α + sin²α = 1⇒ ${\sin }^2\alpha =1-\frac{1}{6}=\frac{5}{6}$

⇒ tan²α = $\frac{{\sin }^2\alpha }{{\cos }^2\alpha }=\frac{\frac{5}{6}}{\frac{1}{6}}$ = 5 và cot²α = $\frac{{\cos }^2\alpha }{{\sin }^2\alpha }=\frac{\frac{1}{6}}{\frac{5}{6}}=\frac{1}{5}$.

⇒ 1 + tan²α = 1 + 5 = 6và 1 + cot²α = 1 + $\frac{1}{5}=\frac{6}{5}$.

Vậy đáp án D đúng.

Câu 27.

Đáp án đúng là: C

Ta có:

P: “Hai tam giác bằng nhau”.

Q: “Hai tam giác đó đồng dạng”.

Ta thấy định lý trên có dạng P ⇒ Q có thể được phát biểu dưới dạng điều kiện cần như sau:

Q là điều kiện cần để có P.

Do đó định lý đã cho được phát biểu dưới dạng điều kiện cần là:

Hai tam giác đồng dạng là điều kiện cần để hai tam giác đó bằng nhau.

Câu 28.

Đáp án đúng là: D

- Trên mặt phẳng Oxy vẽ đường thẳng Δ: x – 3y + 3 = 0 đi qua hai điểm $A\left(1;\frac{4}{3}\right)$ và B(0; 1).

- Xét gốc tọa độ O(0; 0). Ta thấy O không nằm trên đường thẳng Δ và 0 – 3.0 + 3 > 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng bờ là đường thẳng Δ (không kể bờ), chứa gốc tọa độ O.

Câu 29.

Đáp án đúng là: A

+) Vì số nguyên tố là những số chỉ chia hết cho số 1 và chính nó nên 24 không phải là số nguyên tố.

Vì vậy mệnh đề (1) là mệnh đề sai.

+) Ta có: x² – 5x + 9 = 0 có ∆ = (– 5)² – 4 . 9 = – 11 < 0 nên phương trình này vô nghiệm.

Vậy mệnh đề (2) là mệnh đề sai.

+) Vì phương trình x² + 1 = 0 vô nghiệm nên mệnh đề (3) là mệnh đề sai.

+) Mệnh đề (4) là mệnh đề đúng vì số lẻ không chia hết cho 2.

Vậy có 1 mệnh đề đúng.

Câu 30.

Đáp án đúng là: B

Gọi số cây rau cải bạn Vân trồng được là x cây, số cây rau muống bạn Vân trồng được là y cây nên ta có: x ≥ 0; y ≥ 0.

Thời gian Vân trồng x cây rau cải là: 5x (phút)

Thời gian Vân trồng y cây rau muống là: 7y (phút)

Bạn Vân có tối đa 120 phút để trồng rau trong vườn nên ta có: 5x + 7y ≤ 120

Vậy các bất phương trình mô tả điều kiện của bài toán là:

5x + 7y ≤ 120; x ≥ 0; y ≥ 0.

Câu 31.

Đáp án đúng là: A

Trong ∆ABC, ta có 0° < $\frac{A}{2}$ < 90°, và 0° < B < 180°.

Do đó cos $\frac{A}{2}$ > 0, và sin B > 0.

Vậy P = cos $\frac{A}{2}$. sin B > 0.

Câu 32.

Đáp án đúng là: C

Xét tam giác OCD vuông tại D có OD = AB = 55 (m); $\widehat{COD}$ = 60⁰.

Nên CD = OD. tan $\widehat{COD}$ = $55\sqrt{3}$≈ 95,26 (m).

Vậy chiều cao của tháp là: 95,26 + 2 = 97,26 (m).

Câu 33.

Đáp án đúng là: A

Ta có ${\tan }^2\alpha +1=\frac{1}{{\cos }^2\alpha }$

$\Rightarrow {\cos }^2\alpha =\frac{1}{{\tan }^2\alpha +1}=\frac{1}{{\left(-2\sqrt{2}\right)}^2+1}=\frac{1}{9}$

$\Rightarrow \cos \alpha =\pm \frac{1}{3}$

Vì 0° < α < 180° ⇒ sinα > 0 mà $\tan \alpha =-2\sqrt{2}$ nên cosα < 0.

Do đó $\cos \alpha =-\frac{1}{3}$.

Câu 34.

Đáp án đúng là: D

Xét điểm (1; 2) và hệ ta có:

2.1 + 3.2 – 15 = –7 < 0

1 + 2 = 3 > 0

Do đó, điểm (1; 2) nằm trong miền nghiệm của hệ bất phương trình

Câu 35.

Đáp án đúng là: C

Trong tam giác ABC có: $\hat{C}={180}^0-(\hat{A}+\hat{B})={180}^0-({30}^0+{70}^0)={75}^0$

Suy ra tam giác ABC cân tại A, suy ra AB = AC = 5.

Do đó diện tích tam giác ABC là: $S=\frac{1}{2}AB.AC.\sin A=\frac{1}{2}.5.5.\sin {30}^0=\frac{25}{4}$.

III. Hướng dẫn giải chi tiết tự luận

Câu 1.

Hướng dẫn giải

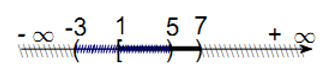
- Biểu diễn tập hợp A trên trục số ta có:

- Biểu diễn tập hợp B trên trục số ta có:

+) Hợp của hai tập hợp A và B là tập hợp các phần tử hoặc thuộc A hoặc thuộc B.

Do đó, A ∪ B = (0; 4).

+) Giao của hai tập hợp A và B là tập hợp các phần tử vừa thuộc A và vừa thuộc B.

Do đó, A ∩ B = (2; 3).

+) Vì hiệu của tập hợp A và B là tập hợp các phần tử thuộc A nhưng không thuộc B.

Mà nhìn vào trục số trên ta thấy nửa khoảng (0; 2] thuộc tập hợp A, không thuộc tập hợp B do đó hiệu của A và B gồm các phần tử nằm trong nửa khoảng (0; 2].

Vậy A \ B = (0; 2].

+ Ta có: C_ℝA = ℝ \ A.

Ta có ℝ \ A là tập hợp tất cả các phần tử thuộc ℝ mà không thuộc tập hợp A.

Vậy C_ℝA = ℝ \ A = (–∞; 0] ∪ [3; +∞).

Câu 2.

Hướng dẫn giải

Gọi x, y lần lượt là số tấn sản phẩm loại A, B mà phân xưởng sản xuất trong 1 ngày (x ≥ 0, y ≥ 0).

Khi đó, số tiền lãi một ngày là: F(x; y) = 2x + 1,6y (triệu đồng).

Số giờ làm việc trong ngày của máy loại 1 là 3x + y.

Số giờ làm việc trong ngày của máy loại 2 là x + y.

Vì máy loại 1 làm việc không quá 6 giờ một ngày, máy loại 2 làm việc không quá 4 giờ 1 ngày nên ta có hệ bất phương trình

Miền nghiệm của hệ bất phương trình là miền tứ giác OABC không bị gạch trong hình vẽ.

Ta có:

F(0; 0) = 2 . 0 + 1,6 . 0 = 0;

F(2; 0) = 2 . 2 + 1,6 . 0 = 4;

F(1; 3) = 2 . 1 + 1,6 . 3 = 6,8;

F(0; 4) = 2 . 0 + 1,6 . 4 = 6,4.

Do đó F(x; y) lớn nhất bằng 6,8 khi (x; y) = (1; 3).

Vậy để thu được lãi lớn nhất phải sản xuất 1 tấn sản phẩm loại A và 3 tấn sản phẩm loại B.

Câu 3.

Hướng dẫn giải

Giả sử tam giác ABC có BC = a, AC = b, AB = c.

Áp dụng công thức tính diện tích tam giác ta có:

$S=\frac{1}{2}ab\sin C=\frac{1}{2}bc\sin A=\frac{1}{2}acsinB.$

Suy ra: $\sin A=\frac{2S}{bc};\sin B=\frac{2S}{ac};\sin C=\frac{2S}{ab}.$

Lại có: $\cos B=\frac{a^2+c^2-b^2}{2ac};\cos C=\frac{a^2+b^2-c^2}{2ab}$; (định lí côsin).

Do đó, ta có:

sin B . cos C + sin C . cos B

$=\frac{2S}{\mathrm{ac}}.\frac{a^2+b^2-c^2}{2\mathrm{ab}}+\frac{2S}{\mathrm{ab}}.\frac{a^2+c^2-b^2}{2\mathrm{ac}}$

$=\frac{S}{a^2\mathrm{bc}}(a^2+b^2-c^2+a^2+c^2-b^2)=\frac{S}{a^2\mathrm{bc}}.2a^2=\frac{2S}{\mathrm{bc}}.\sin A$

Vậy sinA = sin B . cos C + sin C . cos B.

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Năm học 2023

Môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 3)

I. Trắc nghiệm (7 điểm)

Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề?

a) 6x + 1 > 3.

b) Phương trình x² + 3x – 1 = 0 có nghiệm.

c) ∀x ∈ ℝ, 5x > 1.

d) Năm 2018 là năm nhuận.

e) Hôm nay thời tiết đẹp quá!

A. 4;

B. 1;

C. 2;

D. 3.

Câu 2. Cho hai tập hợp A = (1; 4] và B = (2; 5]. Xác định tập hợp A ∩ B.

A. (1; 2);

B. (2; 4);

C. (2; 4];

D. [2; 4).

Câu 3. Tìm mệnh đề phủ định của mệnh đề sau: “Mọi con voi đều không biết bay”.

A. Con voi nào cũng biết bay;

B. Chỉ có một con voi biết bay;

C. Chỉ có một con voi không biết bay;

D.Có ít nhất một con voi biết bay.

Câu 4. Trong các đẳng thức sau đây, đẳng thức nào đúng?

A. $\sin {150}^o=-\frac{\sqrt{3}}{2}$;

B. $\cos {150}^o=\frac{\sqrt{3}}{2}$;

C. $\tan {150}^0=-\frac{1}{\sqrt{3}}$;

D. $\cot {150}^0=\sqrt{3}$.

Câu 5. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

A. 2x² + 3y > 0;

B. x² + y² < 2;

C. x + y² ≥ 0;

D. x + y ≥ 0.

Câu 6. Cho tam giác ABC cóa² + b² – c² > 0. Khi đó:

A. Góc C > 90°;

B. Góc C < 90°;

C. Góc C = 90°;

D. Không thể kết luận được gì về góc C.

Câu 7. Cho hệ bất phương trình:

Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?

A. M(0; 1);

B. N(– 1; 1);

C. P(1; 3);

D. Q(– 1; 0).

Câu8. Tập hợp A = [0; 2] là tập con của tập hợp nào dưới đây?

A. (0; 3);

B. (– 2; 1);

C. (– 1; 2];

D. (– 1; 1).

Câu 9. Trong các cặp số sau đây, cặp nào không thuộc nghiệm của bất phương trình: x – 4y + 5 > 0.

A. (– 5; 0);

B. (– 2; 1);

C. (0; 0);

D. (1; – 3).

Câu 10. Cho $△$ABC với a = 17,4; $\hat{B}$= 44°33'; $\hat{C}$= 64°. Cạnh b bằng bao nhiêu ?

A. 16,5;

B. 12,9;

C. 15,6;

D. 22,1.

Câu 11. Cho góc α tù. Điều khẳng định nào sau đây là đúng?

A. sin α < 0;

B. cos α > 0;

C. tan α > 0;

D. cot α < 0.

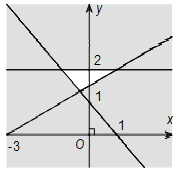
Câu 12. Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm trong hình vẽ của hình vẽ nào, trong các hình vẽ sau?

A. ;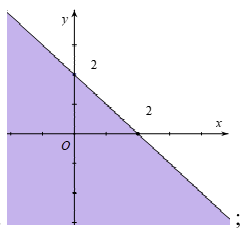

B. ;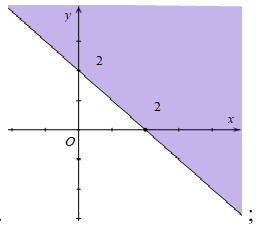

C. ;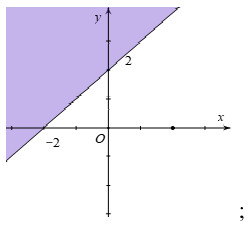

D. .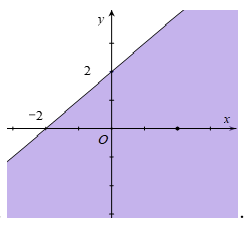

Câu13. Cho tập hợp E = {x ∈ ℤ, |x| ≤ 2}. Tập hợp E được viết dưới dạng liệt kê các phần tử là

A. E = {– 2; – 1; 1; 2};

B. E = {– 1; 0; 1};

C. E = {0; 1; 2};

D. E = {– 2; – 1; 0; 1; 2}.

Câu 14. Trong các câu sau, câu nào là mệnh đề chứa biến?

A. 18 là số chính phương;

B. Hình chữ nhật có hai đường chéo bằng nhau;

C. (x² + x) ⁝ 5, x ∈ ℕ;

D. 9 là số nguyên tố.

Câu 15. Cho tập hợp A = [– 5; 3). Tập C_ℝA là

A. $\left(-\infty ;-5\right)$;

B. $\left(5;+\infty \right)$ ;

C. $[3;+\infty )$;

D. $\left(-\infty ,-5)\cup [3;+\infty \right)$.

Câu 16. Cho DABC vuông tại A, góc B bằng 30°. Khẳng định nào sau đây là sai?

A. $\cos B=\frac{1}{\sqrt{3}}$;

B. $\sin C=\frac{\sqrt{3}}{2}$;

C. $cosC=\frac{1}{2}$;

D. $\sin B=\frac{1}{2}$.

Câu 17. Tam giác ABC có a = 8, c = 3, $\hat{B}$= 60°. Độ dài cạnh b bằng bao nhiêu ?

A. 49;

B. $\sqrt{97}$;

C. 7;

D. $\sqrt{61}$.

Câu 18.Điểm M(0; – 3) thuộc miền nghiệm của hệ bất phương trình nào sau đây?

Câu19. Cho phương trình ax + b = 0. Mệnh đề nào sau đây đúng?

A. Nếu phương trình có nghiệm thì a ≠ 0;

B. Nếu phương trình có nghiệm thì b ≠ 0;

C. Nếu phương trình vô nghiệm thì a = 0;

D. Nếu phương trình vô nghiệm thì b = 0.

Câu 20. Cho tập $A=(-\infty ;-3];B=(2;+\infty );C=(0;4)$ . Khi đó (A$\cup$B)$\cap$C là

A.$\left(x\in R|2\le x\le 4\right)$ ;

B. $\left(x\in R|2<x\le 4\right)$;

C. $\left(x\in R|2<x<4\right)$;

D. $\left(x\in R|2\le x<4\right)$.

Câu 21. Một tam giác có ba cạnh là 13, 14, 15. Diện tích tam giác bằng bao nhiêu ?

A. 84;

B. $\sqrt{84}$;

C. 42;

D. $\sqrt{168}$.

Câu 22. Trong các khẳng định sau, khẳng định nào sai?

A. cos 60° = sin 30°;

B. cos 60° = sin 120°;

C. cos 30° = sin 120°;

D. sin 60° = – cos 120°.

Câu 23. Cặp số (2; 3) là nghiệm của bất phương trình nào sau đây ?

A. 2x – 3y – 1 > 0;

B. x – y < 0;

C. 4x > 3y;

D. x – 3y + 7 < 0.

Câu 24. Tìm mệnh đề sai.

A. Hình thang ABCD nội tiếp đường tròn (O) ⇔ ABCD là hình thang cân;

B. 63 chia hết cho 7 ⇒ Hình bình hành có hai đường chéo vuông góc;

C. Tam giác ABC vuông tại C ⇔ AB² = AC² + BC²;

D. 10 chia hết cho 5 ⇒ Hình vuông có hai đường chéo bằng nhau và vuông góc nhau.

Câu 25. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?

A. $\left(x\in R|x^2-4x+3=0\right)$;

B. $\left(x\in R|6x^2-7x+1=0\right)$;

C. $\left(x\in R|x^2-4x+2=0\right)$;

D. $\left(x\in Z|\left(x\right)<1\right)$.

Câu 26.Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là sai?

A. Tam giác ABC cân thì tam giác có hai cạnh bằng nhau;

B. Số thực a chia hết cho 6 thì a chia hết cho 2 và 3;

C. Tứ giác ABCD là hình bình hành thì AB song song với CD;

D. Tứ giácABCD là hình chữ nhật thì tứ giác có ba góc vuông.

Câu 27. Cho biết $\cos =-\frac{2}{3}$. Tính giá trị của biểu thức $E=\frac{cot\alpha +3\tan \alpha }{2cot\alpha +\tan \alpha }$?

A. $-\frac{19}{13}$;

B. $\frac{19}{13}$;

C. $\frac{25}{13}$;

D. $-\frac{25}{13}$.

Câu 28. Miền nghiệm của hệ bất phương trình 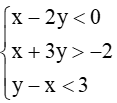là phần không tô đậm của hình vẽ nào trong các hình vẽ sau?

A.

B.

C.

D.

Câu 29. Tam giác với ba cạnh là 5; 12; 13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu ?

A. 2;

B. $2\sqrt{2}$;

C. $2\sqrt{3}$;

D. 3.

Câu 30.Cho bất phương trình 2x + 3y – 6 ≤ 0 (1). Chọn khẳng định đúng trong các khẳng định sau:

A. Bất phương trình (1) chỉ có một nghiệm duy nhất;

B. Bất phương trình (1) vô nghiệm;

C. Bất phương trình (1) luôn có vô số nghiệm;

D. Bất phương trình (1) có tập nghiệm là ℝ.

Câu 31. Trong các hệ thức sau hệ thức nào đúng?

A. ${\sin }^2\alpha +co{s}^2\alpha =1$;

B. ${\sin }^2\alpha +co{s}^2\frac{\alpha }{2}=1$;

C. $\sin {\alpha }^2+cos{\alpha }^2=1$;

D. ${\sin }^{2}2\alpha +co{s}^{2}2\alpha =1$.

Câu 32. Miền nghiệm của bất phương trình: 3(x – 1) + 4(y – 2) < 5x – 3 là nửa mặt phẳng chứa điểm:

A. (0; 0);

B. (– 4; 2);

C. (– 2; 2);

D. (– 5; 3).

Câu 33. Tam giác ABC có a = 6; b = $4\sqrt{2}$; c = 2. M là điểm trên cạnh BC sao cho BM = 3. Độ dài đoạn AM bằng bao nhiêu ?

A. $\sqrt{9}$;

B. 9;

C. 3;

D. $\frac{1}{2}\sqrt{108}$.

Câu 34. Giá trị nhỏ nhất F_min của biểu thức F(x; y) = y – x trên miền xác định bởi hệ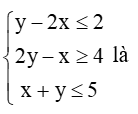

A. F_min = 1;

B. F_min = 2;

C. F_min = 3;

D. F_min = 4.

Câu 35. Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60°. Tàu thứ nhất chạy với tốc độ 30 km/h, tàu thứ hai chạy với tốc độ 40 km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?

A. 13;

B. 15$\sqrt{13}$;

C. 10$\sqrt{13}$;

D. 15.

II. Tự luận (3 điểm)

Câu 1. Cho A = [– 3; 5) ∩ [0; 6), B = (– ∞; 3] ∪ (2; 8].

a) Xác định A, B.

b) Có bao nhiêu số nguyên dương n thỏa mãn “n thuộc tập B và n không thuộc tập A”.

Câu 2. Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm A và sản phẩm B trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm A lãi 4 triệu đồng người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất ra một tấn sản phẩm B lãi được 3 triệu đồng người ta sử dụng máy I trong 6 giờ, máy II trong 3 giờ và máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 36 giờ, máy hai hoạt động không quá 23 giờ và máy III hoạt động không quá 27 giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất.

Câu 3. Cho a², b², c² là độ dài các cạnh của một tam giác nào đó và a, b, c là độ dài các cạnh của tam giác ABC. Khi đó, tam giác ABC là tam giác gì?

-----HẾT------