Bài tập chứng minh đẳng thức vectơ cực hay, có lời giải - Toán lớp 11
Bài tập chứng minh đẳng thức vectơ cực hay, có lời giải
Với Bài tập chứng minh đẳng thức vectơ cực hay, có lời giải Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập chứng minh đẳng thức vectơ từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải
+ Để chứng minh các đẳng thức vecto ta cần sử dụng các quy tắc ba điểm; quy tắc hình hộp; quy tắc hình bình hành; tính chất trọng tâm tam giác hay hệ thức trung điểm đoạn thẳng...
+ Biến đổi vế phức tạp thành vế đơn giản còn lại hoặc chứng minh cả hai vế cùng bằng một biểu thức vecto khác.
B. Ví dụ minh họa
Ví dụ 1: Cho hình lăng trụ tam giác ABC.A’B’C’. Đặt AA'→ = a→, AB→ = b→, AC→ = c→, BC→ = d→. Khẳng định nào dưới đây là đúng ?
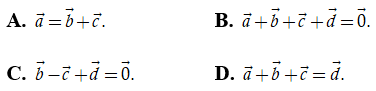
Hướng dẫn giải
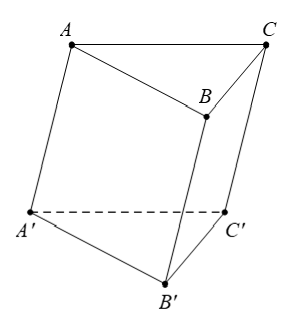
Ta có
Chọn C
Ví dụ 2: Cho hình lập phương ABCD.A’B’C’D’. Gọi O là tâm của hình lập phương. Khẳng định nào dưới đây là đúng ?
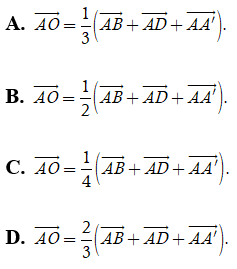
Hướng dẫn giải
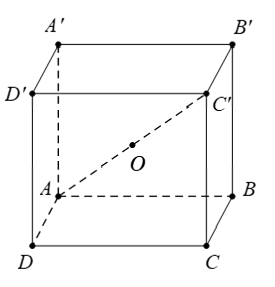
Theo quy tắc hình hộp, ta có AC→ = AB→ + AD→ + AA'→
Mà O là trung điểm của AC’ suy ra
AO→ = (1/2).AC'→ = (1/2).(AB→ + AD→ + AA'→)
Chọn B.
Ví dụ 3: Cho hình hộp ABCD. A’B’C’D’ tâm O. Khẳng định nào dưới đây là sai ?
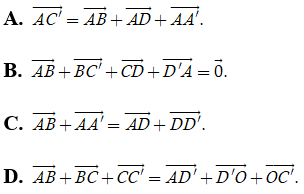
Hướng dẫn giải
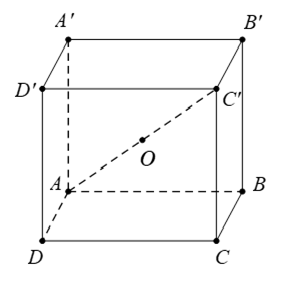
Dựa vào đáp án, ta thấy rằng:
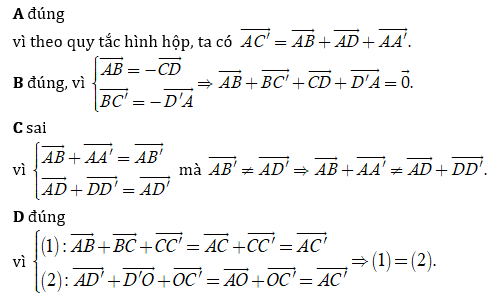
Chọn C
Ví dụ 4: Cho hình hộp ABDC.A1B1C1D1. Khẳng định nào dưới đây là sai ?
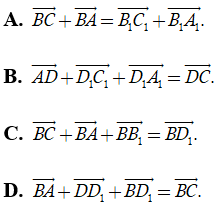
Hướng dẫn giải
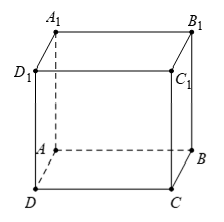
Dựa vào đáp án, ta thấy rằng:
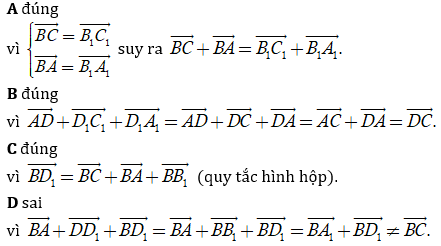
Chọn D
Ví dụ 5: Cho hình hộp ABCD.A1B1C1D1. Gọi M là trung điểm của AD. Khẳng định nào dưới đây là đúng ?
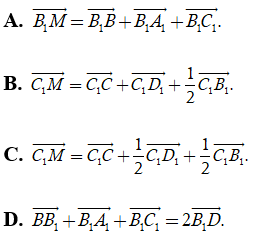
Hướng dẫn giải
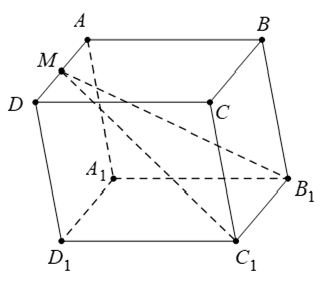
Dựa vào đáp án, ta thấy rằng:
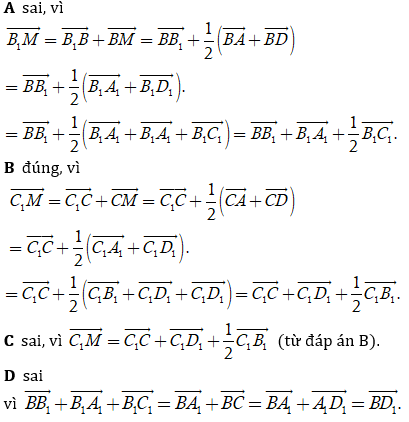
Chọn B

Ví dụ 6: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi G là trọng tâm của tam giác AB’C. Khẳng định nào dưới đây là đúng ?
A. AC'→ = 3AG→
B. AC'→ = 4AG→
C. BD'→ = 4BG→
D. BD'→ = 3BG→
Hướng dẫn giải
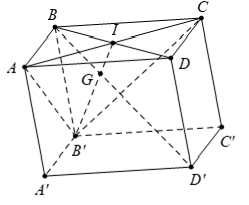
Cách 1. Gọi I là tâm của hình vuông ABCD ⇒ I là trung điểm của BD.
Ta có
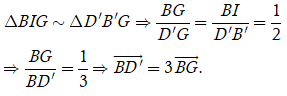
Cách 2. Theo quy tắc hình hộp, ta có 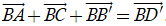
Do G là trọng tâm của tam giác AB’C suy ra
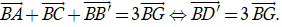
Chọn D
Ví dụ 7: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ MN→ = k.(AC→ + BD→)
A. k = 1/2 B. k = 1/3 C. k = 3 D. k = 2
Hướng dẫn giải
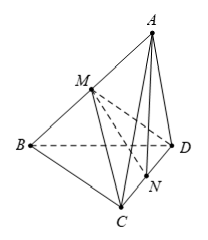

Chọn A
C. Bài tập vận dụng
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt SA→ = a→, SB→ = b→,SC→ = c→, SD→ = d→. Khẳng định nào dưới đây là đúng ?
Lời giải:
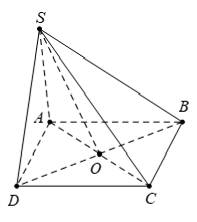
Gọi O là tâm hình bình hành ABCD.
Vì O là trung điểm của AC suy ra
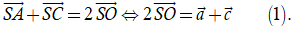
Và O là trung điểm của BD suy ra
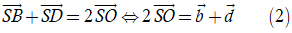
Từ (1) và (2), suy ra a→ + b→ = c→ + d→
Chọn A
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là điểm thỏa mãn GS→ + GA→ + GB→ + GC→ + GD→ = 0→. Khẳng định nào dưới đây là đúng ?
A. G; S; O không thẳng hàng.
B. GS→ = 4OG→
C. GS→ = 5OG→
D. GS→ = 3OG→
Lời giải:
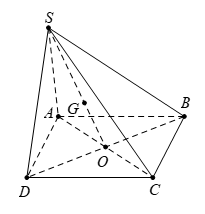
Gọi O là tâm hình bình hành ABCD suy ra
OA→ + OB→ + OC→ + OD→ = 0→
Ta có GS→ + GA→ + GB→ + GC→ + GD→ = 0→ = GS→ + 4GO→ + OA→ + OB→ + OC→ + OD→ = 0→ ⇔ GS→ + 4GO→= 0→ ⇔ GS→ = 4OG→ ⇒ ba điểm G; S, O thẳng hàng
Chọn B.
Câu 3: Cho tứ diện ABCD và điểm G thỏa mãn GA→ + GB→ + GC→ + GD→ = 0→ (G là trọng tâm của tứ diện). Gọi Go là giao điểm của GA và mặt phẳng (BCD). Khẳng định nào dưới đây là đúng ?

Lời giải:
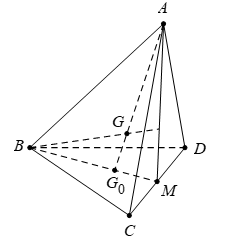
Vì G0 là giao điểm của đường thẳng AG với mặt phẳng (BCD)
Suy ra G0 là trọng tâm của tam giác BCD
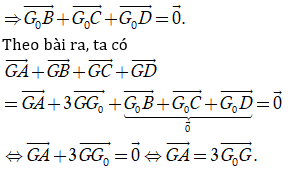
Chọn C

Câu 4: Cho tứ diện ABCD . Gọi M; N lần lượt là trung điểm của AB, CD và G là trung điểm của MN. Khẳng định nào dưới đây là sai ?
Lời giải:
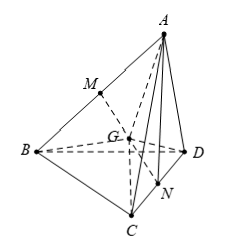
Vì M và N lần lượt là trung điểm của AB; CD suy ra
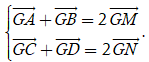
Mà G là trung điểm của MN
⇒ 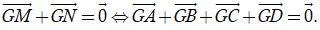
Khi đó
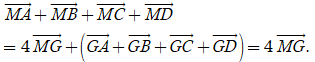
Chọn B.
Câu 5: Cho hình hộp ABCD.A1B1C1D1. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ
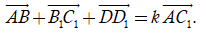
A, k = 4 B. k = 1 C. k = 0 D. k = 2
Lời giải:
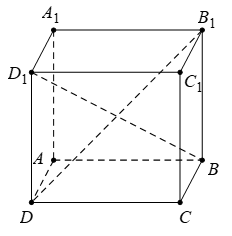
Ta có
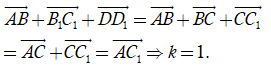
Chọn B
Câu 6: Cho hình hộp ABCD.A’B’C’D’. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ AC→ + BA'→ + k.(DB→ + C'D→) = 0→
A. k = 0 B. k = 1 C. k = 4 D. k = 2
Lời giải:
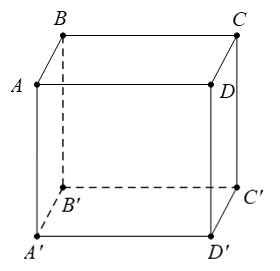
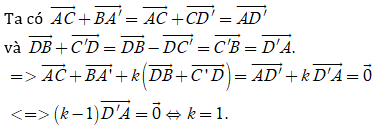
Chọn B.
Câu 7: Gọi M; N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn MN. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ IA→ + (2k - 1)IB→ + k.IC→ + ID→ = 0→
A. k = 2 B. k = 4 C. k = 1 D. k = 0
Lời giải:
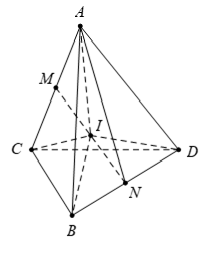
Vì M, N lần lượt là trung điểm của AC, BD
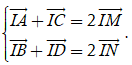
Mặt khác IM→ + IN→ = 0→ (do I là trung điểm của MN) ⇔ IA→ + IB→ + IC→ + ID→ = 0→
Ta có
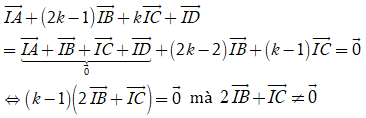
suy ra k - 1 = 0 hay k = 1
Chọn C.
Câu 8: Gọi M, N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn MN và P là một điểm bất kỳ trong không gian. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ PI→ = k(PA→ + PB→ + PC→ + PD→)
A. k = 4 B. k = 1/2 C. k = 1/4 D. k = 2
Lời giải:
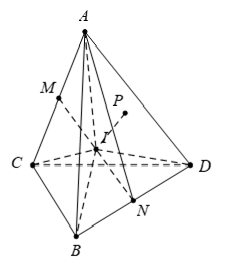
Vì M, N lần lượt là trung điểm của AC, BD
⇒ 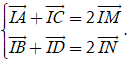
Mặt khác IM→ + IN→ = 0→ (do I là trung điểm của MN) ⇔ IA→ + IB→ + IC→ + ID→ = 0→
Khi đó
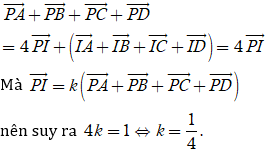
Chọn C