Cách tìm điều kiện để 3 vectơ đồng phẳng hay, chi tiết - Toán lớp 11

---

Cách tìm điều kiện để 3 vectơ đồng phẳng hay, chi tiết

Với Cách tìm điều kiện để 3 vectơ đồng phẳng hay, chi tiết Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm điều kiện để 3 vectơ đồng phẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

* Để chứng minh ba vectơ đồng phẳng, ta có thể chứng minh bằng một trong các cách:

- Chứng minh các giá của ba vectơ cùng song song với một mặt phẳng.

- Dựa vào điều kiện để ba vectơ đồng phẳng: Nếu có m, n ∈ R: c→ = ma→ + nb→ thì a→ ; b→ ; c→ đồng phẳng.

+ Để phân tích một vectơ x ⃗ theo ba vectơ a→; b→; c→ không đồng phẳng, ta tìm các số m, n, p sao cho: x→ = ma→ + nb→ + pc→ .

B. Ví dụ minh họa

Ví dụ 1: Cho hình hộp ABCD.A’B’C’D’. Gọi I và K lần lượt là tâm của hình bình hành ABB’A’ và BCC’B’. Khẳng định nào sau đây sai?

A. IK→ = (1/2)AC→ = (1/2)A'C'→

B. Bốn điểm I; K; C; A đồng phẳng.

C. BD→ + 2IK→ = 2BC→

D. Ba vectơ BD→ ; IK→ ; B'C'→ không đồng phẳng.

Hướng dẫn giải

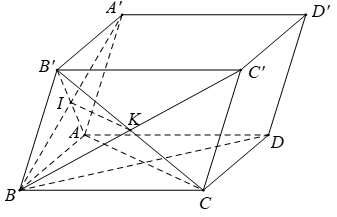
Chọn D.

Ta xét các phương án:

+ A đúng do tính chất đường trung bình trong tam giác A’BC’ và tính chất của hình bình hành ACC’A’.

+ B đúng do IK là đường trung bình của tam giác AB’C nên IK // AC

⇒ bốn điểm I; K; C; A đồng phẳng.

+ C đúng do việc ta phân tích:

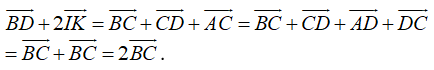
+ D sai do giá của ba vectơ BD→ ; IK→ ; B'C'→ đều song song hoặc trùng với mặt phẳng . Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.

Ví dụ 2: Cho ba vectơ a→ ; b→ ; c→ không đồng phẳng. Xét các vectơ x→ = 2a→ + b→, y→ = a→ - b→ - c→, z→ = -3b→ - 2c→. Chọn khẳng định đúng?

A. Ba vectơ x→, y→, z→ đồng phẳng

B. Ba vectơ x→, a→ cùng phương

C. Ba vectơ x→, b→ cùng phương

D. Ba vectơ x→, y→, z→ đôi một cùng phương

Hướng dẫn giải

Chọn A.

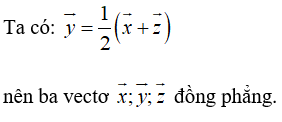
Ví dụ 3: Cho hình hộp ABCD.EFGH. Gọi I là tâm hình bình hành ABEF và K là tâm hình bình hành BCGF. Trong các khẳng định sau, khẳng định nào đúng?

A. BD→, AK→, GF→ đồng phẳng

B. BD→, IK→, GF→ đồng phẳng

C. BD→, EK→, GF→ đồng phẳng

D. BD→, IK→, GC→ đồng phẳng

Hướng dẫn giải

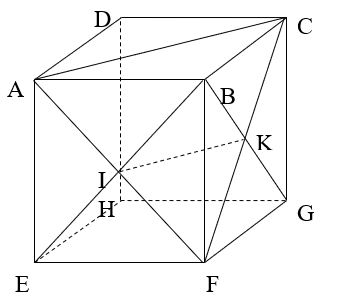
Chọn B.

+ Xét tam giác FAC có I; K lần lượt là trung điểm của AF và FC nên IK là đường trung bình của tam giác.

⇒ IK // AC nên IK // mp (ABCD) .

+ BC // GF nên GF // mp(ABCD)

+

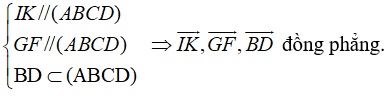
Ví dụ 4: Trong các khẳng định sau, khẳng định nào sai?

A. Nếu giá của ba vectơ a→; b→; c→ cắt nhau từng đôi một thì ba vectơ đó đồng phẳng.

B. Nếu trong ba vectơ a→; b→; c→ có một vectơ 0→ thì ba vectơ đó đồng phẳng.

C. Nếu giá của ba vectơ a→; b→; c→ cùng song song với một mặt phẳng thì ba vectơ đó đồng phẳng.

D. Nếu trong ba vectơ a→; b→; c→ có hai vectơ cùng phương thì ba vectơ đó đồng phẳng.

Hướng dẫn giải

Chọn A.

Ví dụ hình lập phương ABCD.A’B’C’D’ có giá ba vecto AB→; AD→ và AA'→ đôi một cắt nhau nhưng ba vecto đó không đồng phẳng.

Ví dụ 5: Cho hình hộp ABCD.A’B’C’D’. Gọi I và K lần lượt là tâm của hình bình hành ABB’A’ và BCC’B’. Khẳng định nào sau đây sai ?

Hướng dẫn giải

Chọn C

Ví dụ 6: Cho tứ diện ABCD. Trên các cạnh AD và BC lần lượt lấy M; N sao cho AM= 3MD; BN= 3NC. Gọi P; Q lần lượt là trung điểm của AD và BC. Trong các khẳng định sau, khẳng định nào sai?

A. Các vectơ BD→, AC→, MN→ đồng phẳng.

B. Các vectơ MN→, DC→, PQ→ đồng phẳng.

C. Các vectơ AB→, DC→, PQ→ đồng phẳng.

D. Các vectơ AB→, DC→, MN→ đồng phẳng.

Hướng dẫn giải

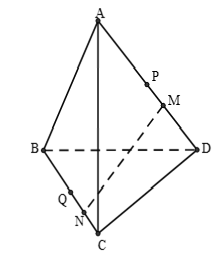
Chọn A

Ví dụ 7: Cho tứ diện ABCD. Gọi M; N lần lượt là trung điểm của AD ; BC. Trong các khẳng định sau, khẳng định nào sai?

A. Các vectơ AB→, DC→, MN→ đồng phẳng

B. Các vectơ AB→, AC→, MN→ không đồng phẳng

C. Các vectơ AN→, CM→, MN→ đồng phẳng

D. Các vectơ BD→, AC→, MN→ đồng phẳng

Hướng dẫn giải

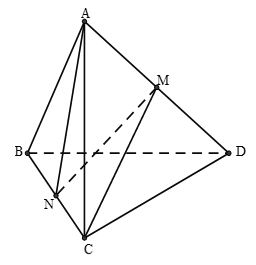
Chọn C.

A. Đúng vì MN→ = (1/2)(AB→ + DC→)

B. Đúng vì từ N ta dựng véctơ bằng véctơ MN→ thì MN→ không nằm trong mặt phẳng ( ABC) .

C. Sai. Tương tự đáp án B thì AN→ không nằm trong mặt phẳng (CMN) .

D. Đúng vì MN→ = (1/2)(AC→ + BD→)

C. Bài tập vận dụng

Câu 1: Cho ba vectơ a→, b→, c→ không đồng phẳng. Trong các khẳng định sau, khẳng định nào sai?

A. Các vectơ x→ = a→ + b→ + 2c→, y→ = 2a→ - 3b→ - 6c→, z→ = -a→ + 3b→ + 6c→ đồng phẳng.

B. Các vectơ x→ = a→ - 2b→ + 4c→, y→ = 3a→ - 3b→ + 2c→, z→ = 2a→ - 3b→ - 3c→ đồng phẳng.

C. Các vectơ x→ = a→ + b→ + c→, y→ = 2a→ - 3b→ + c→, z→ = -a→ + 3b→ + 3c→ đồng phẳng.

D. Các vectơ x→ = a→ + b→ - c→, y→ = 2a→ - b→ + 3c→, z→ = -a→ - b→ + 2c→ đồng phẳng.

Lời giải:

Chọn B

Các vectơ x→, y→, z→ đồng phẳng ⇔ ∃ m, n: x→ = my→ + nz→

+ Xét phương án C :

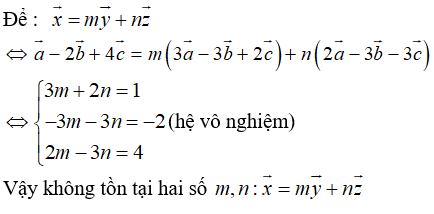
Câu 2: Gọi M ; N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm đoạn MN và P là 1 điểm bất kỳ trong không gian. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ: PI→ = k(PA→ + PB→ + PC→ + PD→)

A. k = 4                  B. k = 1/2                  C. k = 1/4                  D. k = 2

Lời giải:

Chọn C

Do M ; N lần lượt là trung điểm của AC ; BD nên ta có:

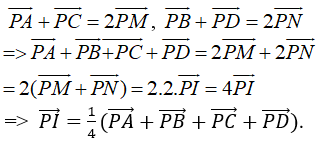
Vậy k = 1/4

Câu 3: Trong các mệnh đề sau đây, mệnh đề nào sai?

A. Vì I là trung điểm đoạn AB nên từ O bất kì ta có: OI→ = (1/2) (OA→ + OB→)

B. Vì AB→ + BC→ + CD→ + DA→ = 0→ nên bốn điểm A : B ; C ; D đồng phẳng

C. Vì NM→ + NP→ = 0→ nên N là trung điểm đoạn NP

D. Từ hệ thức AB→ = 2AC→ - 8AD→ ta suy ra ba vectơ AB→, AC→, AD→ đồng phẳng

Lời giải:

Chọn B.

Do AB→ + BC→ + CD→ + DA→ = 0→ đúng với mọi điểm A : B ; C ; D nên câu B sai

Câu 4: Trong các mệnh đề sau đây, mệnh đề nào đúng?

A. Từ AB→ = 3AC→ ta suy ra BA→ = -3CA→

B. Nếu AB→ = (-1/2)BC→ thì B là trung điểm đoạn AC.

C. Vì AB→ = -2AC→ + 5AD→ nên bốn điểm A ; B ; C ; D đồng phẳng

D. Từ AB→ = -3AC→ ta suy ra CB→ = 2AC→ .

Lời giải:

Chọn C

Ta xét các phương án:

+ Phương án A: Nếu AB→ = 3AC→ thì BA→ = 3CA→ ⇒ A sai.

+ Phương án B: nếu AB→ = (-1/2)BC→ thì A là trung điểm của BC. ⇒ B sai

+ Phương án C:

Ta có: AB→ = -2AC→ + 5AD→

Suy ra: AB→, AC→, AD→ hay bốn điểm A : B ; C ; D đồng phẳng. ⇒ C đúng

+ Nếu AB→ = -3AC→ thì AC→ + CB→ = -3AC→ hay CB→ = -4AC→ nên D sai.

Câu 5: Cho hình chóp S.ABC có M, N, P, Q lần lượt là trung điểm của SC; SB, AB và AC. Tìm mệnh đề sai ?

A. Hai vecto MN→ và PQ→ cùng phương

B. Ba vecto MN→; PQ→ và BC→ đồng phẳng

C. Ba vecto MN→; BC→ và AC→ đồng phẳng

D. A đúng và B sai

Lời giải:

+ Xét tam giác SBC có M và N lần lượt là trung điểm của SC và SB nên MN là đường trung bình của tam giác SBC.

⇒ MN là đường trung bình của tam giác.

⇒ MN // BC; MN = 1/2 BC     (1)

+ Tương tự; ta chứng minh được PQ là đường trung bình của tam giác ABC

⇒ PQ // BC; PQ = 1/2 BC     (2)

Từ (1) và ( 2) suy ra: MN//PQ nên Hai vecto MN→ và PQ→ cùng phương .

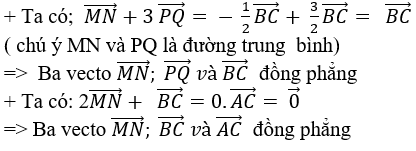
Chọn D