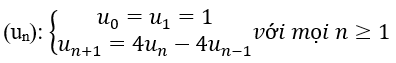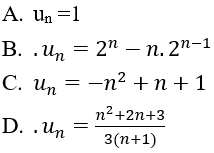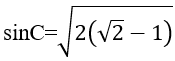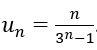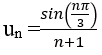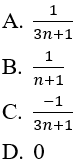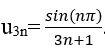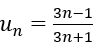60 bài tập trắc nghiệm Dãy số, Cấp số cộng, Cấp số nhân có đáp án - Toán lớp 11

---

60 bài tập trắc nghiệm Dãy số, Cấp số cộng, Cấp số nhân có đáp án

Với 60 bài tập trắc nghiệm Dãy số, Cấp số cộng, Cấp số nhân có đáp án Toán lớp 11 tổng hợp 60 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Dãy số, Cấp số cộng, Cấp số nhân từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

Bài 1: Trong các dãy số sau, dãy nào là cấp số nhân?

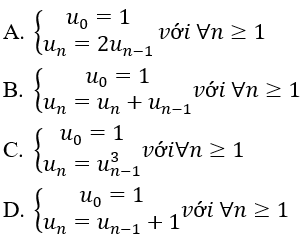
Lời giải:

Đáp án: A

Đáp án A.

Bài 2: Cho 4 số lập thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :

A. 22        B. 166        C. 1752        D. 1408

Lời giải:

Đáp án: D

Đáp án là D

Gọi 4 số lập thành cấp số cộng là u₁,u₂,u₃,u₄

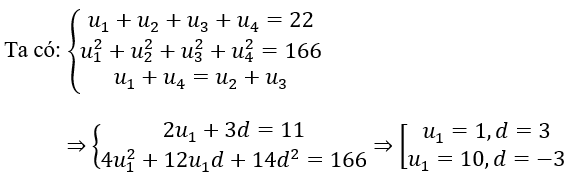
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1

Tổng các lập phương của chúng: 1³+4³+7³+10³=1408

Bài 3: Dùng quy nạp chứng minh mệnh đề chứa biến A(n) đúng với mọi số tự nhiên n > p ( là một số tự nhiên). Ở bước 2 ta giả thiết mệnh đề A(n) đúng với n = k. Khẳng định nào sau đây là đúng?

A. k > p        B. k chia hết cho p

C. k = p        D. k < p

Lời giải:

Đáp án: B

Chọn B.

Bài 4: Cho dãy số (u_n) xác định bởi u_n = n² – 4n – 2. Khi đó u₁₀ bằng:

A. 48        B. 60        C. 58        D. 10

Lời giải:

Đáp án: C

Hướng dẫn giải. u₁₀ = 10² – 4.20 – 2 =58

Đáp án C

Bài 5: Cho dãy số sau. Khi đó số hạng thứ 5 của dãy u_n là:

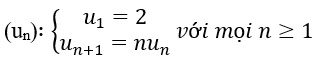
A. 10        B. 48        C. 16        D. 6

Lời giải:

Đáp án: B

u₁=2,u₂=2,u₃=4,u₄=12 ⇒ u₅=4.12=48. Chọn B

Bài 6: Cho cấp số nhân (u_n) có u₁ = 5; u₂ = 8. Tìm u₄

A. 512/25

B. 125/512

C. 625/512

D. 512/125

Lời giải:

Đáp án: A

Bài 6:

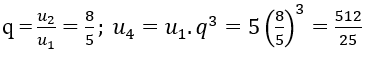
Đáp án A

Bài 7: Cho dãy số sau. Khi đó số hạng thứ 5 của dãy u_n là:

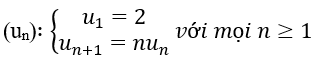
A. 10        B. 48        C. 16        D. 6

Lời giải:

Đáp án: B

Ta có u₂=u₁, u₃=2u₂, u₄=3u₃, u₅=4u₄=48.Chọn B

Bài 8: Trong mặt phẳng toạ độ, cho đồ thị (d) của hàm số y= 4x-5.

Với mỗi số nguyên dương, gọi A_n là giao điểm của(d) và đường thẳng x=n. Xét dãy số (u_n) với u_n là tu_ng độ của điểm A_n. Tính u₁+...+u₁₅.

A. 405        B. 305        C. 205        D. 105

Lời giải:

Đáp án: A

Dễ thấy u_n = 4n -5

Ta có: u_n+1 = 4(n + 1) - 5 = 4n - 1

⇒ u_(n+1)=u_n+4 với n ≥ 1 ⇒ (u_n) là một cấp số cộng với công sai d = 4

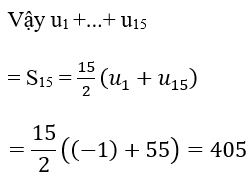
Đáp án là A

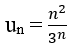
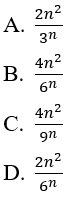
Bài 9: Cho dãy với mọi n ≥ 1. Khi đó số hạng u_2n của dãy u_n là:

Lời giải:

Đáp án: D

Ta có

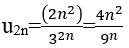
Bài 10: Cho dãy số sau. Công thức của số hạng tổng quát của dãy số là:

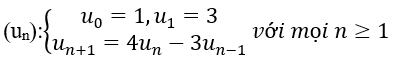
A. u_n = 2n² + 1

B. u_n = 3ⁿ

C. u_n = 2n + 1

Lời giải:

Đáp án: B

Ta có 3ⁿ⁺¹ =4.3ⁿ – 3.3^n-1 ⇒ u_n=3ⁿ. Chọn B

Bài 11: Cho dãy số sau. Công thức của số hạng tổng quát của dãy số là

Lời giải:

Đáp án: B

Ta có 2ⁿ⁺¹ – (n+1)2ⁿ= 4(2ⁿ – n.2^n-1 )- 4(2^n-1 – (n-1)2^n-2)→u_n= 2ⁿ – n.2^n-1

Chọn B

Bài 12: Cho tam giác ABC cân (AB=AC), có cạnh đáy BC, đường cao AH, cạnh bên AB theo thứ tự số đo lập thành một cấp số nhân. Hãy tính công bội q của cấp số nhân đó.

Lời giải:

Đáp án: C

Theo giả thiết AB=AC, BC,AH,AB lập thành cấp số nhân nên ta có hệ:

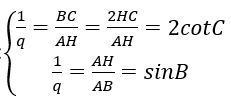
Từ đó ta có kết quả sau: 2cotC = sinC ⇔ 2cosC =sin²C = 1-cos²C ⇔ cos²C + 2cosC -1 =0 ⇒ cosC = -1 +√2 (0º< C < 90º)

Do C là góc nhọn nên

Cho nên công bội của cấp số nhân là:

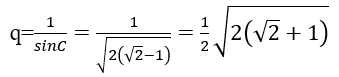
Đáp án C.

Bài 13: Cho dãy số (u_n) biết u₁ = (-1)ⁿ.5²ⁿ⁺⁵ Mệnh đề nào sau đây đúng?

A. Dãy số u_n bị chặn trên và không bị chặn dưới.

B. Dãy số u_n bị chặn dưới và không bị chặn trên.

C. Dãy số u_n bị chặn.

D. Dãy số u_n không bị chặn.

Lời giải:

Đáp án: D

Nếu n chẵn thì u_n = 5²ⁿ⁺⁵ > 0 tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn nên dãy u_n không bị chặn trên.

Nếu n lẻ thì u_n = -5²ⁿ⁺⁵ < 0 giảm xuống vô hạn (âm vô cùng) khi n tăng lên vô hạn nên dãy u_n không bị chặn dưới.

Vậy dãy số đã cho không bị chặn. Chọn D.

Bài 14: Tìm x biết 1+3 +5+...+x =64

A. 9        B. 11        C. 15        D. 17

Lời giải:

Đáp án: B

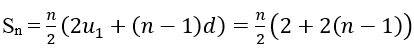
=n² = 64 ⇒ n=8

Vậy x=u_n=u₁+(n-1)d=1+7.2=15

Đáp án C.

Bài 15: Cho dãy số sau. Dãy số bị chặn trên bởi số nào dưới đây?

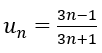
A. 1/3        B. 1        C.1/2        D.0

Lời giải:

Đáp án: B

Ta có

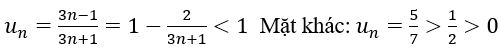
nên suy ra dãy u_n bị chặn trên bởi số 1. Chọn B.

Bài 16: Cho các dãy số sau:

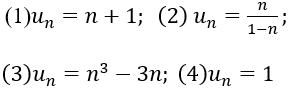
Khẳng định nào dưới đây là đúng?

A. (1) dãy đơn điệu tăng; (2) là dãy đơn điệu giảm; (3) là dãy đơn điệu tăng;(4) là dãy đơn điệu tăng

B. (1) dãy đơn điệu tăng; (2) là dãy đơn điệu giảm; (3) là dãy đơn điệu tăng;(4) là dãy không đơn điệu

C. (1) dãy đơn điệu tăng; (2) là dãy đơn điệu tăng; (3) là dãy không đơn điệu ;(4) là dãy không đơn điệu

D. Đáp án khác

Lời giải:

Đáp án: C

Dễ dàng có được đáp án. Chọn C

Bài 17: Cho các dãy số (u_n), (v_n), (x_n), (y_n) lần lượt xác định bởi:

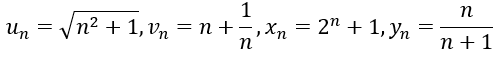
Trong các dãy số trên có bao nhiêu dãy bị chặn dưới

A. 1        B. 2        C. 3        D. 4

Lời giải:

Đáp án: D

Ta có

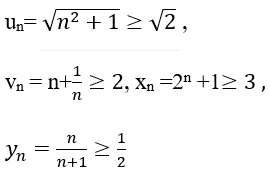
nên cả bốn dãy số đều bị chặn dưới. Chọn D

Bài 18: Tìm các số (x,y) biết y < 0 và các số x+6y, 5x+2y, 8x+y theo thứ tự lập thành cấp số cộng đồng thời các số x+ 5/3, y -1, 2x – 3y theo thứ tự đó lập thành một cấp số nhân.

A. (3, -1)        B. (-3, -1)        C. (-1,-3)        D. (-1,3)

Lời giải:

Đáp án: B

Ta có hệ phương trình:

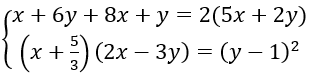
Từ đó ta suy ra

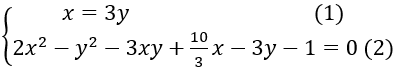
Thế (1) vào (2) ta được: 8y²+7y-1=0⇒y=-1 hoặc y=1/8

Do y < 0 , ta được y = -1, x = -3

Đáp án B

Bài 19: Cho dãy số (u_n) biết u_n=(-1)ⁿ.2n Mệnh đề nào sau đây sai?

A. u₁=-2        B. u₂=4        C. u₃=-6        D. u₄=-8

Lời giải:

Đáp án: D

Thay trực tiếp hoặc dùng chức năng CALC: u₁=-2.1=-2;u₂=(-1)².2.2=4;u₃=(-1)³.2.3=6;u₄=(-1)⁴.2.4=8. Chọn D.

Bài 20: Cho hai cấp số cộng(un): 4,7,10,13,16,...và (v_n):1,6,11,16,21,...Hỏi trong 100 số hạng đầu tiên của mỗi cấp số cộng , có bao nhiêu số hạng chung?

A. 10        B. 20        C. 30        D. 40

Lời giải:

Đáp án: B

Ta có: un = 4+(n-1).3 = 3n+1, 1 ≤ n ≤ 100

v_n = 1+ (k-1).5 = 5k -4, 1 ≤ k ≤ 100

Để một số là số hạng chung của hai cấp số cộng ta phải có:

3n +1 =5k -4 ⇔3n = 5(k-1)⇒ n⋮5 tức là n = 5t, k =1 + 3t, t ∈ Z

Vì 1 ≤ n ≤ 100 nên 1 ≤ t ≤ 20. Có 20 số hạng chung của hai dãy

Chọn đáp án B

Bài 21: Ba số x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1 đồng thời các số x, 2y, 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0. Tìm giá trị của q.

A. q = 1/3        B. q = 1/9        C. q = -1/3        D. q = -3

Lời giải:

Đáp án: A

Ta có: y = qx, z = x. q². Vì x, 2y, 3z lập thành CSC nên ta có:

x + 3 x. q²=2.2qx ⇔ 1 + 3q²=4q ⇔q=1(loại) hoặc q = 1/3.

Đáp án A.

Bài 22: Cho dãy số sau. Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào dưới đây?

Lời giải:

Đáp án: B

Dùng MTCT chức năng CALC: ta có u₁=1/2;u₂=1/4;u₃=3/26

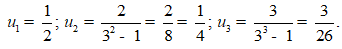
Bài 23: Cho dãy số sau. Tìm số hạng u₅

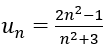
A. u₅=1/4        B. u₅=17/12        C. u₅=7/4        D. u₅=71/39

Lời giải:

Đáp án: C

Thế trực tiếp hoặc dùng chức năng CALC: u₅=49/28=7/4 Chọn C.

Bài 24: Trong các dãy số sau dãy số nào là cấp số nhân?

A. 1,3,5,7,9

B. -1,-3,1,3,5

C. 1,2,4,16,256

D. 1,2,4,8,16

Lời giải:

Đáp án: D

Đáp án D (CSN với công bội là 2).

Bài 25: Nếu các số 5 + m, 7 + 2m, 17 + m theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu?

A. m = 2        B. m = 3        C. m = 4        D.m = 5

Lời giải:

Đáp án: C

các số 5 + m, 7 + 2m, 17 + m theo thứ tự lập thành cấp số cộng nên:

5 + m + 17 + m = 2(7 + 2m) ⇔ m = 4.

Đáp án C.

Bài 26: Mặt sàn tầng một ngôi nhà cao hơn mặt sân 0,5m. Cầu thang đi tầng 1 lên tầng 2 gồm 21 bậc, mỗi bậc cao 18cm. Độ cao của tầng hai so với mặt sân là:

A. 4,10m        B. 4,28m        C. 1,89m        D. 1,8m

Lời giải:

Đáp án: B

Độ cao tầng hai so với mặt sàn là h = (0,5+ 0,18n) (m) với n = 21. Vậy ta có độ cao tầng 2 bằng 4,28m

Đáp án B

Bài 27: Dùng quy nạp chứng minh mệnh đề chứa biến A(n) đúng với mọi số tự nhiên n ≥ p (p là một số tự nhiên). Ở bước 1 (bước cơ sở) của chứng minh quy nạp, bắt đầu với n bằng:

A. n = 1        B. n = p        C. n > p        D. n ≥ p

Lời giải:

Đáp án: B

Chọn B.

Bài 28: Một học sinh chứng minh mệnh đề "8ⁿ+1 chia hết cho 7 mọi n ∈ ¥" như sau:

Giả sử (*) đúng với n = k, tức là 8ⁿ+1 chia hết cho 7

Ta có: 8^(k+1)+1=8(8^k+1)-7 , kết hợp với giả thiết 8^k+1 chia hết cho 7 nên suy ra được 8^(k+1)+1 chia hết cho 7 Vậy đẳng thức đúng với mọi n ∈ ¥

Khẳng định nào sau đây là đúng?

A. Học sinh trên chứng minh đúng.

B. Học sinh chứng minh sai vì không có giả thiết qui nạp.

C. Học sinh chứng minh sai vì không dùng giả thiết qui nạp.

D. Học sinh không kiểm tra bước 1 (bước cơ sở) của phương pháp qui nạp.

Lời giải:

Đáp án: D

Thiếu bước 1 là kiểm tra với n = 1, khi đó ta có 8 +1 = 9 không chi hết cho 7. Chọn D.

Bài 29: Ba số hạng đầu của một cấp số nhân là x – 6, x và y .Tìm y, biết rằng công bội của cấp số nhân là 6

A. y = 216        B. y = 216/5        C. y = 1296/5        D. y = 12

Lời giải:

Đáp án: B

Ta có x = 6(x – 6) ⇔ x = 7.2. Từ đó suy ra y = 6x = 43.2.

Đáp án B.

Bài 30: Trong các dãy số sau, dãy nào là dãy số nhân?

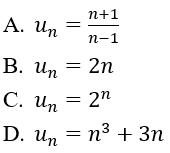
Lời giải:

Đáp án: C

Đáp án C vì

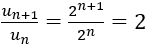
Bài 31: Trong các dãy số (u_n) sau đây, dãy số nào là dãy số bị chặn?

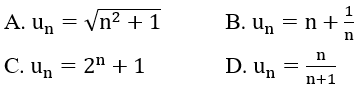
Lời giải:

Đáp án: D

Các dãy số n²;n;2ⁿ dương và tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn,

nên các dãy 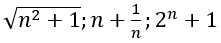cũng tăng lên vô hạn (dương vô cùng), suy ra các dãy này không bị chặn trên, do đó chúng không bị chặn. Chọn D.

Nhận xét:

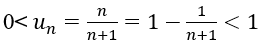
Bài 32: Trong các dãy số sau, dãy nào là cấp số cộng?

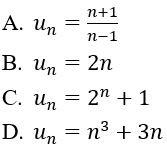
Lời giải:

Đáp án: B

Đáp án B. Ta có u_n+1-u_n=2(n+1)-2n=2. Đây là CSC với công sai d = 2.

Bài 33: Trong các dãy số (u_n) cho bởi số hạng tổng quát u_n sau, dãy số nào bị chặn?

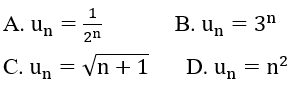
Lời giải:

Đáp án: A

Các dãy số n²;n;3ⁿ dương và tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn

nên các dãy 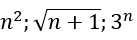cũng tăng lên vô hạn (dương vô cùng), suy ra các dãy này không bị chặn trên, do đó chúng không bị chặn. Chọn A.

Bài 34: Trong các dãy số (u_n) cho bởi số hạng tổng quát u_n sau, dãy số nào bị chặn trên?

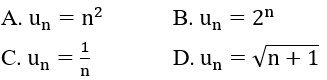
Lời giải:

Đáp án: C

Các dãy số n²;2ⁿ;n+1 là các dãy tăng đến vô hạn khi n tăng lên vô hạn nên chúng không bị chặn trên (có thể dùng chức năng TABLE của MTCT để kiểm tra). Chọn C.

Bài 35: Thêm hai số thực dương x và y vào giữa hai số 5 và 320 để được bốn số 5,x,y,320 theo thứ tự đó lập thành cấp số nhân. Khẳng định nào sau đây là đúng?

Lời giải:

Đáp án: B

Bốn số 5, x, y, 320 theo thứ tự lập thành cấp số nhân nên ta có:

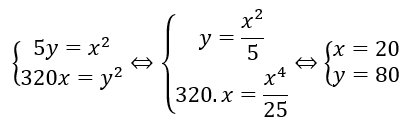
Đáp án B.

Bài 36: Số hạng đầu tiên của cấp số nhân (u_n) thoả mãn hệ

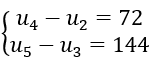
A. 2        B. 12        C. 24        D. 0

Lời giải:

Đáp án: B

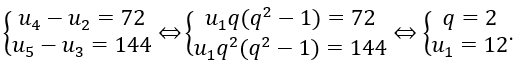
Đáp án B.

Bài 37: Cho dãy số (u_n) xác định bởi u_n = n² – 4n – 2. Khi đó u₁₀ bằng:

A. 48        B. 60        C. 58        D. 10

Lời giải:

Đáp án: C

Hướng dẫn giải. u₁₀ = 102 – 4.20 – 2 =58.

Đáp án C

Bài 38: Người ta trồng 3003 cây theo hình tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ 2 có 2 cây, hàng thứ 3 có 3 cây,...Vậy có tất cả bao nhiêu hàng?

A. 75        B. 76        C. 77        D. 78

Lời giải:

Đáp án: C

Gọi số hàng cần tìm là n. Ta có các hàng cây lập thành CSC với công sai d = 1 và số hạng đầu là 1.

Khi đó:

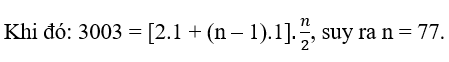
Đáp án C.

Bài 39: Cho dãy số u_n = 1+ (n +3).3ⁿ. khi đó công thức truy hồi của dãy là:

A. u_n+1 = 1 +3u_n với n ≥ 1

B. u_n+1 = 1 +3u_n + 3ⁿ⁺¹ với n ≥ 1

C. u_n+1 = u_n + 3ⁿ⁺¹ - 2 với n ≥ 1

D. u_n+1 = 3u_n + 3ⁿ⁺¹ - 2 với n ≥ 1

Lời giải:

Đáp án: D

Hướng dẫn giải. u_n+1 = 1+ (n+4).3ⁿ⁺¹ = 1 + (n+3).3ⁿ⁺¹ + 3ⁿ⁺¹

= 1 + 3ⁿ.(n+3).3 + 3ⁿ⁺¹ = 3[1 + (n+ 3).3ⁿ] + 3ⁿ⁺¹ – 2 = 3u_n + 3ⁿ⁺¹ -2

Đáp án là D

Bài 40: Cho dãy số (u_n) xác định bởi

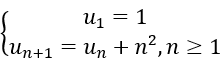
Công thức của u_n+1 theo n là:

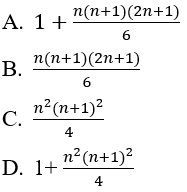
Lời giải:

Đáp án: A

Hướng dẫn giải.

u₁ = 1

u₂ = 1 + 12

u₃ = 1 + 12 + 22

u₄ = 1 + 12 + 22 + 32

...

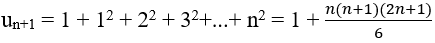
(có thể chứng minh bằng quy nạp). Đáp án A

Bài 41: Cho cấp số cộng (u_n) có u₃ = 15 và d = -2. Tìm u_n

Lời giải:

Đáp án: A

u₃ = 15 = u₁ – 2.2 ⇒ u₁ = 19. Vậy u_n=-2n+19.

Đáp án A.

Bài 42: Cho ba số tạo thành một cấp số nhân mà tổng của chúng bằng 93. Ta có thể sắp xếp chúng (theo thứ tự của cấp số nhân kế trên) như là số hạng thứ nhất, thứ hai và thứ bảy của một cấp số cộng. Tìm tích của 3 số đó.

A. 3375        B. 64        C. 2744        D. 1000

Lời giải:

Đáp án: A

Gọi 3 số cần tìm là a, b, c. Vì 3 số trên là số hạng thứ nhất, thứ hai và thứ bảy của một cấp số cộng

nên ta có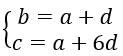

(với d là công sai của cấp số cộng đó).

3 số trên tạo thành cấp số nhân với tổng là 93 nên ta có:

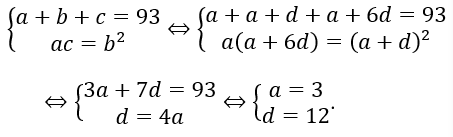
Vậy a = 3, b = 15, c = 75. Tích ba số trên là 3.15.75 = 3375.

Đáp án A.

Bài 43: Cho dãy số dưới với mọi n ≥ 1. Khi đó số hạng u_3n của dãy (u_n) là:

Lời giải:

Đáp án: D

Ta có

Bài 44: Công sai của cấp số cộng (u_n) thoả mãn

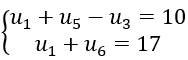
A. 0        B. -1        C. -2        D. -3

Lời giải:

Đáp án: D

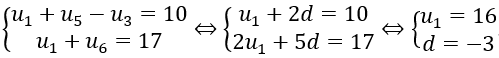
Bài 45: Cho dãy số (u_n) , biết

Dãy số (u_n) bị chặn trên bởi số nào dưới đây?

A. 1/3        B.1        C.1/2        D.10

Lời giải:

Đáp án: B

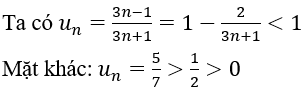
nên suy ra dãy (u_n) bị chặn trên bởi số 1. Chọn B.

Bài 46: Cho cấp số nhân có các số hạng lần lượt là x, 12, y, 192 Mệnh đề nào sau đây là đúng?

A. x = 1, y = 144.        B. x = 2, y = 72

C. x =3, y = 48        D. x = 4, y = 36

Lời giải:

Đáp án: C

Cấp số nhân có các số hạng lần lượt là x, 12, y, 192 nên ta có:

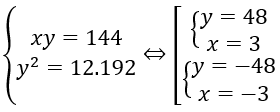
Đáp án C.

Bài 47: Trong các dãy số (u_n) cho bởi số hạng tổng quát u_n sau, dãy số nào là dãy số tăng?

Lời giải:

Đáp án: D

Vì 2ⁿ;n là các dãy dương và tăng nên 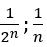là các dãy giảm, do đó loại các đáp án A và B.

Xét đáp án C:

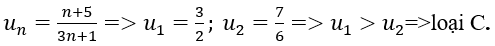
Bài 48: Tìm số hạng đầu của cấp số nhân có bốn số hạng, biết tổng ba số hạng đầu bằng 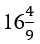, đồng thời theo thứ tự, chúng là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng.

A. 4        B. 16/9        C. 2/3        D. -1

Lời giải:

Đáp án: A

Gọi 4 số cần tìm là a, b, c, d. Vì 3 số hạng đầu là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng nên ta có

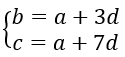
(với d là công sai của cấp số cộng đó).

Từ giả thiết ta có:

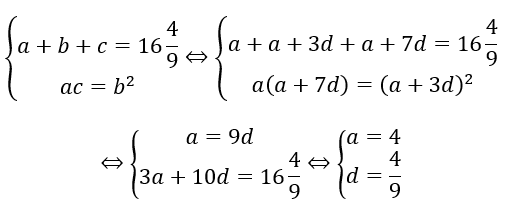
Vậy số hạng đầu là 4. Đáp án A.

Bài 49: Trong các dãy số (u_n) cho bởi số hạng tổng quát u_n sau, dãy số nào là dãy số giảm?

Lời giải:

Đáp án: C

u_n = sin n có thể dương hoặc âm phụ thuộc n nên đáp án A sai. Hoặc dễ thấy sin ⁡n có dấu thay đổi trên ¥ nên dãy sin⁡n không tăng, không giảm.

B.

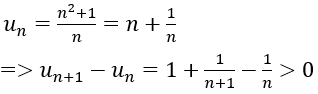
nên dãy đã cho tăng nên B sai.

C.

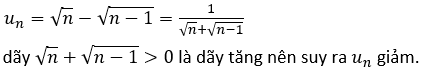
Chọn C.

Bài 50: Số hạng đầu tiên của cấp số cộng dương (u_n) thoả mãn

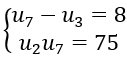
A. 2        B. 3        C. 4        D. 5

Lời giải:

Đáp án: B

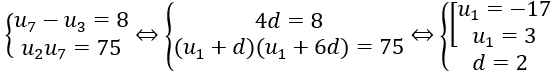
ĐÁp án B.

Bài 51: Tìm x dương để các số 2, 8, x, 128 theo thứ tự đó lập thành một cấp số nhân.

A. x = 14        B. x = 32        C. x = 64        D. x = 68

Lời giải:

Đáp án: B

Vì 8, x, 128 theo thứ tự đó lập thành một cấp số nhân nên ta có:

x²=8.128 ⇒ x=±36.

Đáp án B.

Bài 52: Cho dãy số z_n = 1 + (4n – 3).2ⁿ

A. Dãy z_n là dãy tăng

B. Dãy z_n bị chặn dưới

C. Cả A và B đề sai

D. Cả A và B đều đúng

Lời giải:

Đáp án: B

Hướng dẫn giải. u_n = n² – 4n + 7 = (n -2)² + 3 ≥ 3

⇒ (u_n) bị chặn dưới bởi 3

(u_n) không bị chặn trên bởi vì n càng lớn thì u_n càng lớn

Đáp án là B

Bài 53: Cho dãy số u_n = n² – 4n + 7. Kết luận nào đúng?

A. Dãy (u_n) bị chặn trên

B. Dãy (u_n) bị chặn dưới

C. Dãy (u_n) bị chặn

D. Các mệnh đề A,B,C đều sai

Lời giải:

Đáp án: D

Hướng dẫn giải. z_n+1 = 1 + (4n+1).2ⁿ⁺¹; z_n = 1 + (4n-3).2ⁿ

⇒ z_n+1-z_n=2ⁿ (4n+5) > 0 ∀n ∈ N*

⇒ (z_n) tăng ⇒ z_n ≥ z₁=3 ∀n ∈ N*

Đáp án là D

Bài 54: Cho 3 số x, 3, y lập thành một cấp số nhân và x⁴=y√3. Tìm công bội q của cấp số đó

A. 1/3        B. √3        C. 3        D. 1/√3

Lời giải:

Đáp án: B

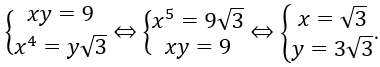
Vậy công bội q = √3.

Đáp án B.

Bài 55: Tìm m nguyên để phương trình x⁴-(3m+5) x²+(m+1)²=0 có bốn nghiệm lập thành một cấp số cộng (giả sử phương trình trên đã có bốn nghiệm phân biệt)

A. m=1        B. m=5        C. m=3/2        D. m=25/4

Lời giải:

Đáp án: B

x⁴-(3m+5) x²+(m+1)²=0 (1)

Đặt x²=t. Ta có phương trình trên có dạng:

t²-(3m+5)t+(m+1)²=0 (2)

Giả sử a, b là hai nghiệm dương phân biệt của phương trình (2) và a > b.

Khi đó 4 nghiệm của phương trình (1) sẽ là: -√a,-√b,√b,√a. Vì 4 nghiệm trên theo thứ tự lập thành CSC nên ta có:

-√a+√b=-2√b ⇔ a=9b.

Theo Viet ta có:

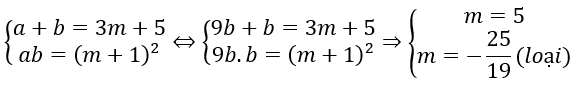
Đáp án B.

Bài 56: Xác định số đo góc nhỏ nhất của một tứ giác lồi, biết rằng số đo 4 góc lập thành một cấp số cộng và góc lớn nhất bằng 5 lần góc nhỏ nhất.

A. 30º        B. 45º        C. 15º        D. 60º

Lời giải:

Đáp án: A

Gọi 4 góc đó lập thành cấp số cộng là u₁,u₂,u₃,u₄

Ta có:

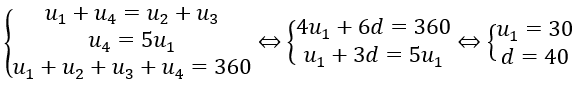
Đáp án A.

Bài 57: Khi sử dụng phương pháp quy nạp để chứng minh mệnh đề chứa biến A(n) đúng với mọi số tự nhiên n > p (p là một số tự nhiên), ta tiến hành hai bước:

- Bước 1, kiểm tra mệnh đề A(n) đúng với n = p

- Bước 2, giả thiết mệnh đề A(n) đúng với số tự nhiên bất kỳ n > p và phải chứng minh rằng nó cũng đúng với n = k+1

Trong hai bước trên:

A. Chỉ có bước 1 đúng.        B. Chỉ có bước 2 đúng.

C. Cả hai bước đều đúng.        D. Cả hai bước đều sai.

Lời giải:

Đáp án: C

Đáp án C.

Bài 58: Một học sinh chứng minh mệnh đề "8ⁿ+1 chia hết cho 7 mọi n ∈ ¥" (*) như sau:

- Giả sử đúng với n = k, tức là 8ⁿ+1 chia hết cho 7

- Ta có: 8^k+1+1=8(8^k+1)-7 , kết hợp với giả thiết 8^k+1 chia hết cho 7 nên suy ra được 8^k+1+1 chia hết cho 7 Vậy đẳng thức đúng với mọi n ∈ ¥

Khẳng định nào sau đây là đúng?

A. Học sinh trên chứng minh đúng.

B. Học sinh chứng minh sai vì không có giả thiết qui nạp.

C.Học sinh chứng minh sai vì không dùng giả thiết qui nạp.

D. Học sinh không kiểm tra bước 1 (bước cơ sở) của phương pháp qui nạp.

Lời giải:

Đáp án: D

Thiếu bước 1 là kiểm tra với n = 1, khi đó ta có 8 +1 = 9 không chi hết cho 7. Chọn D.

Bài 59: Dùng quy nạp chứng minh mệnh đề chứa biến A(n) đúng với mọi số tự nhiên n ≥ p (p là một số tự nhiên). Ở bước 1 (bước cơ sở) của chứng minh quy nạp, bắt đầu với n bằng:

A. n = 1        B. n = p        C. n > p        D. n ≥ p

Lời giải:

Đáp án: B

Đáp án B.

Bài 60: Cho phương trình: x³ + 3x² – (24+m)x -26 –n= 0. Tìm hệ thức liên hệ giữa m và n để 3 nghiệm phân biệt x₁,x₂,x₃ lập thành một cấp số cộng (giả sử phương trình đã cho có 3 nghiệm phân biệt)

A. 3m = n

B. m = 3n

C. m = n

D. m + n = 0

Đáp án và hướng dẫn giải

Lời giải:

Đáp án: C

Vì 3 nghiệm phân biệt x₁,x₂,x₃ lập thành một cấp số cộng và dùng hệ thức Viet cho phương trình bậc 3. Ta có:

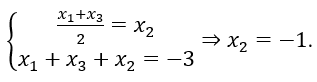
Vậy phương trình có 1 nghiệm là 1. Thay vào phương trình ta có:

-1 + 3 + (24+m) – 26 – n = 0 ⇔ m = n.

Đáp án C.