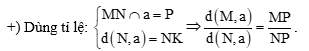Khoảng cách từ một điểm tới một đường thẳng, mặt phẳng lớp 11 (bài tập + lời giải)

---

Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Khoảng cách từ một điểm tới một đường thẳng, mặt phẳng lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Khoảng cách từ một điểm tới một đường thẳng, mặt phẳng.

Khoảng cách từ một điểm tới một đường thẳng, mặt phẳng lớp 11 (bài tập + lời giải)

1. Phương pháp giải

1.1. Xác định khoảng cách từ điểm đến đường thẳng

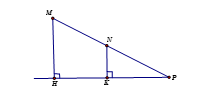
Bước 1: Xác định hình chiếu H của điểm M đến đường thẳng a

+) Trong mặt phẳng chứa M và a, kẻ MH $\perp$ a tại H.

+) Dựng (P) chứa M và vuông góc a tại H ⇒ MH $\perp$ a tại H.

Bước 2: Sử dụng các công thức tính độ dài đoạn thẳng để tính MH:

+) $△$MHN vuông tại H: MH² = MN² – NH².

+) $△$MAB vuông tại M có MH là đường cao:

$\frac{1}{M{H}^2}=\frac{1}{M{A}^2}+\frac{1}{M{B}^2}$

$MH=\frac{MA.MB}{AB}=\frac{MA.MB}{\sqrt{M{A}^2+M{B}^2}}$.

+) $△$MAB có MH là đường cao: $S_{MAB}=\frac{1}{2}.AB.MH\Rightarrow MH=\frac{2.S_{MAB}}{AB}$ .

1.2. Xác định khoảng cách từ điểm đến mặt phẳng

Xác định hình chiếu của điểm lên mặt phẳng

Cách 1: Dựng trực tiếp: AM $\perp$ (P) tại M ⇒ d(A, (P)) = AM.

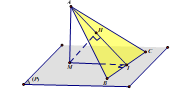
Cách 2: Dựng hình chiếu từ chân đường vuông góc

Ta có AM$\perp$ (P) và BC $\subset$ (P) nên AM $\perp$ BC (1).

Trong (P), dựng MI $\perp$BC (2).

Từ (1) và (2), suy ra BC $\perp$ (AMI).

Trong (AMI), dựng MH$\perp$ AI.

Có MH $\subset$ (AMI) và BC $\perp$(AMI) nên BC $\perp$ MH.

Vì BC $\perp$ MH và MH $\perp$ AI nên MH$\perp$ (ABC).

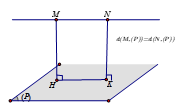
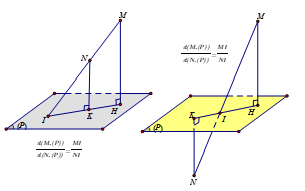
Cách 3: Sử dụng tính chất song song: MN // (P) ⇒ d(M, P) = d(N, (P)).

Cách 4: Sử dụng tỉ lệ: $MN\cap \left(P\right)=I\Rightarrow \frac{d\left(M,\left(P\right)\right)}{d\left(N,\left(P\right)\right)}=\frac{MI}{NI}$.

2. Ví dụ minh họa

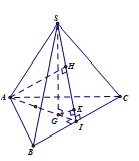
Ví dụ 1. Cho hình chóp S.ABC tất cả cách cạnh bằng 2a, SG $\perp$ (ABC) với G là trọng tâm DABC, I là trung điểm BC.

a) Tính khoảng cách từ S đến AI.

b) Tính khoảng cách từ A đến SI.

Hướng dẫn giải:

a) Ta có SG $\perp$ (ABC) ⇒ SG$\perp$AI ⇒ d(S, AI) = SG.

Vì DABC đều, AI là trung tuyến nên AI đồng thời là đường cao và $AI=\frac{2a\sqrt{3}}{2}=a\sqrt{3}$ .

Vì G là trọng tâm nên

Xét DSAG vuông tại G có:

$SG=\sqrt{S{A}^2-A{G}^2}=\sqrt{{\left(2a\right)}^2-{\left(\frac{2\sqrt{3}}{3}a\right)}^2}=\frac{2\sqrt{6}}{3}a$.

Vậy $d\left(S,AI\right)=SG=\frac{2\sqrt{6}}{3}a$ .

b) Trong (SAI): Vẽ AH$\perp$SI tại H ⇒ d(A, SI) = AH,

Vẽ GK $\perp$ SI tại K ⇒ d(G, SI) = GK .

Ta có: $AG\cap SI=I\Rightarrow \frac{d\left(A,SI\right)}{d\left(G,SI\right)}=\frac{AI}{GI}\Rightarrow d\left(A,SI\right)=AH=\frac{AI}{GI}.GK$ .

Có $GI=\frac{1}{3}AI=\frac{a\sqrt{3}}{3}$ .

Xét $△$SGI vuông tại G, có: $\frac{1}{G{K}^2}=\frac{1}{S{G}^2}+\frac{1}{G{I}^2}=\frac{3}{8a^2}+\frac{3}{a^2}=\frac{27}{8a^2}\Rightarrow GK=\frac{2a\sqrt{6}}{9}$ .

$\Rightarrow AH=\frac{AI}{GI}\cdot GK=\frac{3}{1}.\frac{2\sqrt{6}}{9}a=\frac{2\sqrt{6}}{3}a$

Vậy $d\left(A,SI\right)=\frac{2\sqrt{6}}{3}a$ .

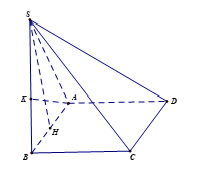
Ví dụ 2. Cho hình chóp S.ABCD có đáy hình vuông cạnh a, DSAB đều và nằm trong mặt phẳng vuông góc với đáy.

a) Tính khoảng cách từ S đến (ABCD).

b) Tính khoảng cách từ A đến (SBC).

Hướng dẫn giải:

a) Gọi H là trung điểm của AB.

Vì DSAB đều nên SH $\perp$AB và $SH=\frac{a\sqrt{3}}{2}$.

Mà (SAB) $\perp$ (ABCD) và (SAB) $\cap$ (ABCD) = AB nên SH $\perp$(ABCD).

Do đó d(S, (ABCD)) = SH $=\frac{a\sqrt{3}}{2}$ .

b) Vì SH $\perp$ (ABCD) nên SH $\perp$BC mà BC$\perp$ AB nên BC $\perp$(SAB).

Kẻ AK $\perp$ SB tại K.

Vì BC$\perp$(SAB) nên BC $\perp$ AK mà AK$\perp$SB nên AK $\perp$ (SBC).

Do đó d(A, (SBC)) = AK $=\frac{a\sqrt{3}}{2}$ .

3. Bài tập tự luyện

Bài 1. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), DABC là tam giác đều cạnh a, SA = 2a. Khoảng cách từ A đến mặt phẳng (SBC) bằng

A. $\frac{\sqrt{57}a}{3}$;

B. $\frac{2\sqrt{57}a}{19}$;

C. $\frac{2\sqrt{57}a}{3}$;

D. $\frac{\sqrt{57}a}{12}$.

Bài 2. Cho hình chóp S.ABCD có đáy là hình bình hành với $BC=a\sqrt{2},\widehat{ABC}=60°$ . Tam giác SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ điểm D đến mặt phẳng (SAB) bằng

A. $\frac{a\sqrt{6}}{2}$;

B. $\frac{a\sqrt{2}}{2}$;

C. $a\sqrt{2}$;

D. $\frac{2a\sqrt{6}}{3}$.

Bài 3. Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách từ A đến mặt phẳng (BCD) bằng

A. $\frac{a\sqrt{6}}{2}$;

B. $\frac{a\sqrt{3}}{3}$;

C. $\frac{2a\sqrt{6}}{3}$;

D. $\frac{a\sqrt{6}}{3}$.

Bài 4. Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau, AB = a, AC = b, AD = c. Khoảng cách từ điểm A đến mặt phẳng (BCD) bằng

A. $\frac{1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}}$;

B. $\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}$ ;

C. $\sqrt{a^2+b^2+c^2}$;

D. $\frac{1}{\sqrt{a^2+b^2+c^2}}$.

Bài 5. Cho lăng trụ ABC.A'B'C' có đáy là tam giác vuông cân tại A với AB = AC = 3a. Hình chiếu vuông góc của B' lên mặt đáy là điểm H thuộc BC sao cho HC = 2HB. Biết cạnh bên của lăng trụ bằng 2a. Khoảng cách từ B đến mặt phẳng (B'AC) bằng

A. $\frac{2a}{\sqrt{3}}$;

B. $a\sqrt{3}$ ;

C. $\frac{3a\sqrt{3}}{2}$;

D. $\frac{a}{2}$.

Bài 6. Cho hình chóp S.ABCD có SA $\perp$ (ABCD), SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.

A. $\frac{a\sqrt{2}}{4}$;

B. $\frac{a\sqrt{3}}{3}$ ;

C. $\frac{a\sqrt{3}}{4}$;

D. $\frac{a\sqrt{2}}{3}$.

Bài 7. Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a², BC = a. Khoảng cách từ S đến BC bằng bao nhiêu?

A. 2a;

B. 4a;

C. 3a;

D. 5a.

Bài 8. Cho hình chóp A.BCD có cạnh AC $\perp$ (BCD) và BCD là tam giác đều cạnh bằng a. Biết  $AC=a\sqrt{2}$ và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng

A. $a\sqrt{\frac{7}{5}}$;

B. $a\sqrt{\frac{4}{7}}$ ;

C. $a\sqrt{\frac{6}{11}}$ ;

D. $a\sqrt{\frac{2}{3}}$ .

Bài 9. Cho tứ diện SABC trong đó SA, SB, SC vuông góc với nhau từng đôi một và SA = 3a, SB = a, SC = 2a. Khoảng cách từ A đến đường thẳng BC bằng:

A. $\frac{3a\sqrt{2}}{2}$;

B. $\frac{7a\sqrt{5}}{5}$ ;

C. $\frac{8a\sqrt{3}}{3}$ ;

D. $\frac{5a\sqrt{6}}{6}$ .

Bài 10. Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng a. Khoảng cách từ tâm của đáy đến một cạnh bên bằng

A. $a\sqrt{2}\cot \alpha$ ;

B. $a\sqrt{2}\tan \alpha$ ;

C. $\frac{a\sqrt{2}}{2}\cos \alpha$ ;

D. $\frac{a\sqrt{2}}{2}\sin \alpha$ .