Bài toán thực tế về thể tích lớp 11 (bài tập + lời giải)

---

Chuyên đề phương pháp giải Bài toán thực tế về thể tích lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm Bài toán thực tế về thể tích.

Bài toán thực tế về thể tích lớp 11 (bài tập + lời giải)

1. Phương pháp giải

Để làm tốt dạng bài này, các em cần nắm vững các công thức liên quan đến tính thể tích của hình chóp, hình lăng trụ, hình lập phương, hình hộp chữ nhật…và vận dụng các công thức một cách linh hoạt trong các bài toán.

2. Ví dụ minh họa

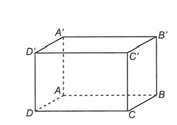
Ví dụ 1. Một tấm bìa hình vuông có cạnh 50 cm. Người ta cắt bỏ đi ở bốn góc tấm bìa hình vuông cạnh 16 cm rồi gấp lại thành một cái hộp chữ nhật không có nắp. Tính thể tích khối hộp chữ nhật.

Hướng dẫn giải:

Theo đề bài, ta có AA' = BB' = CC' = DD' = 16 cm.

Khi đó ABCD là hình vuông có cạnh AB = 50 – 2.16 = 18 cm.

Do đó V_{ABCD.A'B'C'D'} = AB.AB.AA' = 18.18.16 = 5184 cm³.

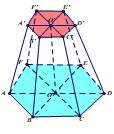
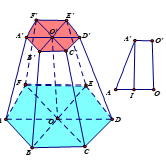
Ví dụ 2. Để tạo nên một chiếc lồng đèn hình chóp cụt đều như hình bên dưới cần dùng 3 loại thanh tre có độ dài lần lượt là 30 cm, 60 cm, 90 cm, sao cho lồng đèn cao nhất có thể. Tính thể tích lồng đèn này.

Hướng dẫn giải:

Vì để lồng đèn cao nhất nên thanh 90 cm được dùng làm cạnh bên, các thanh 30 cm, 60 cm lần lượt dùng làm các cạnh đáy lớn và đáy nhỏ của hình chóp cụt.

$h=A^{\text{'}}I=\sqrt{{90}^2-{\left(60-30\right)}^2}=60\sqrt{2}\left(cm\right)$.

$S=S_{ABCDEF}=6\cdot \frac{\sqrt{3}}{4}\cdot {60}^2=5400\sqrt{3}\left(c{m}^2\right)$.

$S^{\text{'}}=S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}{E}^{\text{'}}{F}^{\text{'}}}=6\cdot \frac{\sqrt{3}}{4}\cdot {30}^2=1350\sqrt{3}\left(c{m}^2\right)$.

$\Rightarrow V=\frac{1}{3}h\cdot \left(S+S^{\text{'}}+\sqrt{S{S}^{\text{'}}}\right)=189000\sqrt{6}\left(c{m}^3\right)$.

3. Bài tập tự luyện

Bài 1. Một hồ bơi hình hộp chữ nhật có đáy là hình vuông cạnh bằng 50 m. Lượng nước trong hồ cao 1,5m. Thể tích nước trong hồ là:

A. 3750 m³;

B. 2500 m³;

C. 1250 m³;

D. 1875 m³.

Bài 2. Một khối gỗ có dạng là lăng trụ, biết diện tích đáy và chiều cao lần lượt là 0,25 m² và 1,2 m. Mỗi mét khối gỗ này trị giá 5 triệu đồng. Hỏi khối gỗ đó có giá trị bao nhiêu tiền?

A. 750 000 đồng;

B. 500 000 đồng;

C. 1 500 000 đồng;

D. 3 000 000 đồng.

Bài 3. Từ một tấm bìa hình vuông người ta cắt ở bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng 6 cm, rồi gập tấm bìa lại để được một chiếc hộp không nắp có dạng hình hộp chữ nhật. Tính cạnh của tấm bìa ban đầu, biết rằng thể tích của chiếc hộp bằng 600 cm³.

A. 22 cm;

B. 10 cm;

C. 10 dm;

D. 22 dm.

Bài 4. Một thùng đựng rác có dạng khối chóp cụt tứ giác đều với hai cạnh đáy lần lượt là 2 dm và 3 dm, chiều cao bằng 4 dm. Tính thể tích của thùng đựng rác.

A. 76 dm²;

B. $\frac{76}{3}$  dm²;

C. 76 dm³;

D. $\frac{76}{3}$  dm³.

Bài 5. Một chiếc bánh chưng có dạng khối hộp chữ nhật với kích thước ba cạnh là 15 cm, 15 cm và 6 cm. Tính thể tích của chiếc bánh chưng đó.

A. 1350 cm²;

B. $\frac{1350}{2}$  cm²;

C. 1350 cm³;

D. $\frac{1350}{2}$  cm³.

Bài 6. Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12 cm. Tính khối lượng của miếng pho mát theo đơn vị gam, biết khối lượng riêng của loại pho mát đó là 3g/cm³.

A. 2160 g;

B. 2106 g;

C. 720 g;

D. 702g.

Bài 7. Người ta muốn xây một bồn chứa nước dạng khối hộp chữ nhật trong một phòng tắm. Biết chiều dài, chiều rộng và chiều cao của khối hộp đó là 5 m, 1m, 2m. Biết mỗi viên gạch có chiều dài 20 cm, chiều rộng 10 cm, chiều cao 5 cm. Hỏi người ta sử dụng ít nhất bao nhiêu viên gạch để xây bồn đó và thể tích thực của bồn chứa là bao nhiêu? (giả sử lượng xi măng và cát không đáng kể).

A. 1180 viên, 8820 lít;

B. 1182 viên, 8800 lít;

C. 1180 viên, 8800 lít;

D. 1182 viên, 8820 lít.

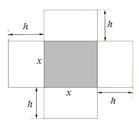
Bài 8. Một hộp không nắp được làm từ một mảnh bìa các tông như hình vẽ. Hộp có đáy là một hình vuông cạnh x (cm), chiều cao h (cm) và thể tích là 500 cm³. Tính độ dài cạnh hình vuông x sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.

A. x = 5 cm;

B. x = 10 cm;

C. x = 2 cm;

D. x = 3 cm.

Bài 9. Tính thể tích khối rubic mini (mỗi mặt của rubic có 9 ô vuông), biết chu vi mỗi ô (ô hình vuông trên một mặt) là 4 cm.

A. 27 cm³;

B. 1728 cm³;

C. 1 cm³;

D. 9 cm³.

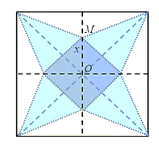
Bài 10. Cắt một miếng giấy hình vuông và xếp thành một hình chóp tứ giác đều như hình vẽ. Biết cạnh của hình vuông bằng 20 cm, OM = x (cm). Tìm x để hình chóp đều ấy có thể tích lớn nhất.

A. x = 9cm;

B. x = 8cm;

C. x = 6cm;

D. x = 7cm.