Lý thuyết Cấp số nhân hay, chi tiết nhất - Toán lớp 11

Lý thuyết Cấp số nhân hay, chi tiết nhất

Tài liệu Lý thuyết Cấp số nhân hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Cấp số nhân từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

I. ĐỊNH NGHĨA

Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.

Số q được gọi là công bội của cấp số nhân.

Nếu (u_n) là cấp số nhân với công bội q, ta có công thức truy hồi:

    u_n+1 = u_nq với n ∈ N^*

Đặc biệt:

    + Khi q = 0, cấp số nhân có dạng u₁, 0, 0,…, 0,…

    + Khi q = 1, cấp số nhân có dạng u₁, u₁, u₁,…, u₁,…

    + Khi u₁ = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0,…, 0…

II. SỐ HẠNG TỔNG QUÁT

Định lí 1

Nếu cấp số nhân có số hạng đầu u₁ và công bội q thì số hạng tổng quát u_n được xác định bởi công thức

    u_n = u₁.q^n-1 với n ≥ 2

III. TÍNH CHẤT CÁC SỐ HẠNG CỦA CẤP SỐ NHÂN

Định lí 2

Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là

    u_k² = u_k-1.u_k+1 với k ≥ 2

IV. TỔNG n SỐ HẠNG ĐẦU TIÊN CỦA MỘT CẤP SỐ NHÂN

Định lí 3

Cho cấp số nhân (u_n) với công bội q ≠ 1. Đặt S_n = u₁ + u₂ + … + u_n. Khi đó

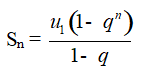
Chú ý: Nếu q = 1 thì cấp số nhân là u₁, u₁, u₁,…, u₁,… khi đó S_n = nu₁.