Lý thuyết Hàm số liên tục hay, chi tiết nhất - Toán lớp 11

Lý thuyết Hàm số liên tục hay, chi tiết nhất

Tài liệu Lý thuyết Hàm số liên tục hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Hàm số liên tục từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

I. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM

Định nghĩa 1

    Cho hàm số y = f(x) xác định trên khoảng K và x₀ ∈ K.

    Hàm số y = f(x) được gọi là liên tục tại x₀ nếu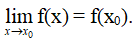

II. HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG

Định nghĩa 2

    Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.

    Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và

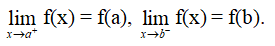
Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.

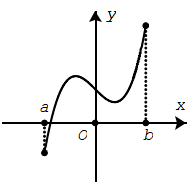
Hàm số liên tục trên khoảng (a;b)

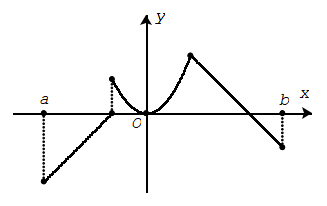
Hàm số không liên tục trên khoảng (a; b).

III. MỘT SỐ ĐỊNH LÍ CƠ BẢN

Định lí 1

    a) Hàm số đa thức liên tục trên toàn bộ tập số thực R.

    b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.

Định lí 2

    Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x₀. Khi đó:

    a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x₀;

    b) Hàm số 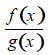liên tục tại x₀ nếu g(x₀) ≠ 0.

Định lí 3

    Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0..

Định lí 3 có thể phát biểu theo một dạng khác như sau:

    Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).