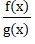Lý thuyết Tổng hợp chương Giới hạn hay, chi tiết nhất - Toán lớp 11

---

Lý thuyết Tổng hợp chương Giới hạn hay, chi tiết nhất

Tài liệu Lý thuyết Tổng hợp chương Giới hạn hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Tổng hợp chương Giới hạn từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

GIỚI HẠN CỦA DÃY SỐ

I. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ

1. Định nghĩa

Định nghĩa 1

    Ta nói dãy số (u_n) có giới hạn là 0 khi n dần tới dương vô cực, nếu |u_n| có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.

    Kí hiệu: 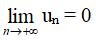hay u_n → 0 khi n → +∞.

Định nghĩa 2

    Ta nói dãy số (v_n) có giới hạn là a (hay v_n dần tới a) khi n → +∞ nếu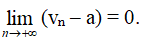

    Kí hiệu: 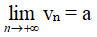hay v_n → a khi n → +∞.

2. Một vài giới hạn đặc biệt

a) 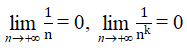với k nguyên dương;

b) 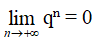nếu |q| < 1;

c) Nếu u_n = c (c là hằng số) thì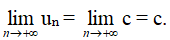

Chú ý: Từ nay về sau thay cho 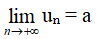ta viết tắt là lim u_n = a.

II. ĐỊNH LÝ VỀ GIỚI HẠN HỮU HẠN

Định lí 1

a) Nếu lim u_n = a và lim v_n = b thì

    lim (u_n + v_n) = a + b

    lim (u_n – v_n) = a – b

    lim (u_n.v_n) = a.b

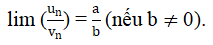
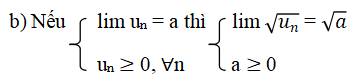
III. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN

Cấp số nhân vô hạn (u_n) có công bội q, với |q| < 1 được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn:

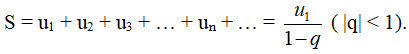
IV. GIỚI HẠN VÔ CỰC

1. Định nghĩa

    - Ta nói dãy số (u_n) có giới hạn là +∞ khi n → +∞, nếu u_n có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

    Kí hiệu: lim u_n = +∞ hay u_n → +∞ khi n → +∞.

    - Dãy số (u_n) có giới hạn là –∞ khi n → +∞, nếu lim (–u_n) = +∞.

    Kí hiệu: lim u_n = –∞ hay u_n → –∞ khi n → +∞.

Nhận xét: u_n = +∞ ⇔ lim(–u_n) = –∞

2. Một vài giới hạn đặc biệt

Ta thừa nhận các kết quả sau

a) lim n^k = +∞ với k nguyên dương;

b) lim qⁿ = +∞ nếu q > 1.

3. Định lí 2

a) Nếu lim u_n = a và lim v_n = ±∞ thì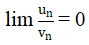

b) Nếu lim u_n = a > 0, lim v_n = 0 và v_n > 0, ∀ n > 0 thì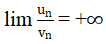

c) Nếu lim u_n = +∞ và lim v_n = a > 0 thì

GIỚI HẠN CỦA HÀM SỐ

I. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM

1. Định nghĩa

Định nghĩa 1

    Cho khoảng K chứa điểm x₀ và hàm số y = f(x) xác định trên K hoặc trên K \ {x₀}.

    Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x₀ nếu với dãy số (x_n) bất kì, x_n ∈ K \{x₀} và x_n → x₀, ta có f(x_n) → L.

    Kí hiệu: 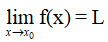hay f(x) → L khi x → x₀.

Nhận xét: 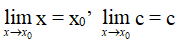với c là hằng số.

2. Định lí về giới hạn hữu hạn

Định lí 1

3. Giới hạn một bên

Định nghĩa 2

    - Cho hàm số y = f(x) xác định trên (x₀; b).

    Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x₀ nếu với dãy số (x_n) bất kì, x₀ < x_n < b và x_n → x₀, ta có f(x_n) → L.

    Kí hiệu: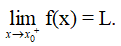

    - Cho hàm số y = f(x) xác định trên (a; x₀).

    Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x₀ nếu với dãy số (x_n) bất kì, a < x_n < x₀ và x_n → x₀, ta có f(x_n) → L.

    Kí hiệu: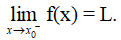

Định lí 2

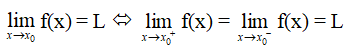
II. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC

Định nghĩa 3

a) Cho hàm số y = f(x) xác định trên (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → +∞ nếu với dãy số (x_n) bất kì, x_n > a và x_n → +∞, ta có f(x_n) → L.

Kí hiệu: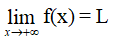

b) Cho hàm số y = f(x) xác định trên (–∞; a).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → –∞ nếu với dãy số (x_n) bất kì, x_n < a và x_n → –∞, ta có f(x_n) → L.

Kí hiệu: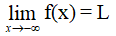

Chú ý:

a) Với c, k là hằng số và k nguyên dương, ta luôn có:

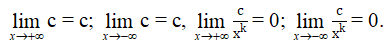
b) Định lí 1 về giới hạn hữu hạn của hàm số khi x → x₀ vẫn còn đúng khi x_n → +∞ hoặc x → –∞

III. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ

1. Giới hạn vô cực

Định nghĩa 4

Cho hàm số y = f(x) xác định trên (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là –∞ khi x → +∞ nếu với dãy số (x_n) bất kì, x_n > a và x_n → +∞, ta có f(x_n) → –∞

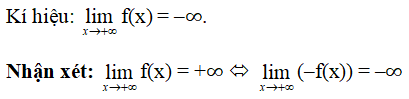
2. Một vài giới hạn đặc biệt

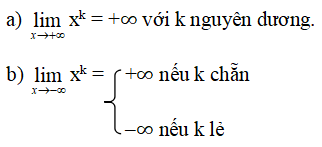
3. Một vài quy tắc về giới hạn vô cực

a) Quy tắc tìm giới hạn của tích f(x).g(x)

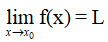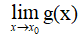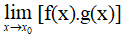L > 0	+∞	+∞
	–∞	–∞
L < 0	+∞	–∞
	–∞	+∞

b) Quy tắc tìm giới hạn của thương

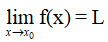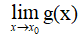		Dấu của g(x)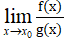
L	± ∞	Tùy ý	0
L > 0	0	+∞	+∞
		–∞	–∞
L < 0		+∞	–∞
		–∞	+∞

HÀM SỐ LIÊN TỤC

I. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM

Định nghĩa 1

    Cho hàm số y = f(x) xác định trên khoảng K và x₀ ∈ K.

    Hàm số y = f(x) được gọi là liên tục tại x₀ nếu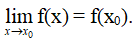

II. HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG

Định nghĩa 2

    Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.

    Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và

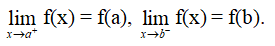
III. MỘT SỐ ĐỊNH LÍ CƠ BẢN

Định lí 1

    a) Hàm số đa thức liên tục trên toàn bộ tập số thực R.

    b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.

Định lí 2

    Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x₀. Khi đó:

    a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x₀;

    b) Hàm số 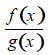liên tục tại x₀ nếu g(x₀) ≠ 0.

Định lí 3

    Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0..

Định lí 3 có thể phát biểu theo một dạng khác như sau:

    Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).