Tìm ảnh của một điểm qua phép đối xứng tâm cực hay - Toán lớp 11
Tìm ảnh của một điểm qua phép đối xứng tâm cực hay
Với Tìm ảnh của một điểm qua phép đối xứng tâm cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm ảnh của một điểm qua phép đối xứng tâm từ đó đạt điểm cao trong bài thi môn Toán lớp 11.
A. Phương pháp giải
Biểu thức toạ độ của phép đối xứng tâm
Trong hệ tọa độ Oxy:
• Nếu tâm đối xứng là O(0;0), với mỗi M(x;y) gọi M' = DO(M) = (x';y') thì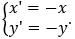 
• Nếu tâm đối xứng I(a;b) bất kì, với mỗi M(x;y) gọi M' = DI(M) = (x';y') thì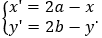 
B. Ví dụ minh họa
Ví dụ 1: Trong mặt phẳng tọa độ Oxy. Tìm ảnh của điểm M(-2020;2019) qua phép đối xứng tâm O(0;0)
Hướng dẫn giải:
Biểu thức tọa độ của phép đối xứng tâm O(0;0) là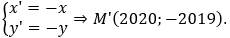 
Ví dụ 2: Trong mặt phẳng tọa độ Oxy. Tìm ảnh của điểm M(2;–1) qua phép đối xứng tâm I(1;2) là:
Hướng dẫn giải:
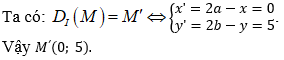
Ví dụ 3: Trong mặt phẳng Oxy, biết M'(5;3) là ảnh của M qua phép đối xứng tâm I(4;1). Tìm tọa độ điểm M.
Hướng dẫn giải:
+ Giải sử M(x,y). Thay biểu thức tọa độ của phép đối xứng tâm I(4;1) ta được: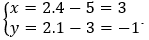 
Ví dụ 4: Trong mặt phẳng Oxy, Cho M(3;7) và M'(5;3). Biết M’ là ảnh của M qua phép đối xứng tâm I. Tìm tọa độ điểm I.
Hướng dẫn giải:
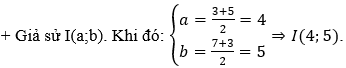
C. Bài tập trắc nghiệm
Câu 1. Trong mặt phẳng Oxy, cho điểm I(x0;y0). Gọi M(x;y) là một điểm tùy ý và M'(x';y') là ảnh của M qua phép đối xứng tâm I. Khi đó biểu thức tọa độ của phép đối xứng tâm I là:
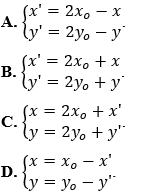
Lời giải:
Chọn A
+ I(x0;y0) là trung điểm của MM'nên có: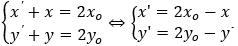 
Câu 2. Trong mặt phẳng tọa độ Oxy cho phép đối xứng tâm O(0;0) biến điểm M(-2;3) thành điểm M'có tọa độ là:
A. M'(-4;2).
B. M'(2;-3).
C. M'(-2;3).
D. M'(2;3).
Lời giải:
.
Biểu thức tọa độ của phép đối xứng tâm O(0;0) là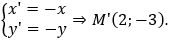 
Chọn B.
Câu 3. Ảnh của điểm M(3;–1) qua phép đối xứng tâm I(1;2) là:
A. (2; 1).
B. (–1; 5).
C. (–1; 3).
D. (5;–4).
Lời giải:
Chọn B
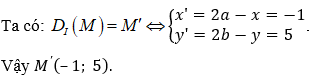
Câu 4. Trong mặt phẳng Oxy, ảnh của điểm A(5;3) qua phép đối xứng tâm I(4;1) là:
Lời giải:
Chọn C
+ Thay biểu thức tọa độ của phép đối xứng tâm I(4;1) ta được: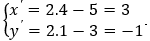 
Câu 5. Trong mặt phẳng tọa độ Oxy cho phép đối xứng tâm I(1;2) biến điểm M(x;y) thành M'(x';y'). Mệnh đề nào sau đây là đúng?
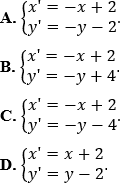
Lời giải:
.
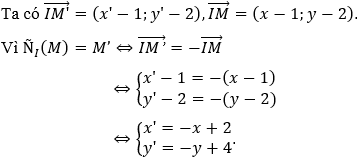
Chọn B.
Câu 6. Trong mặt phẳng Oxy. Phép đối xứng tâm O(0;0) biến điểm M(–2;3) thành điểm:
A. M'(–4;2).
B. M'(2;–3).
C. M'(–2;3).
D. M'(2;3).
Lời giải:
Chọn B
+ Thay biểu thức tọa độ của phép đối xứng tâm O(0;0) ta có :
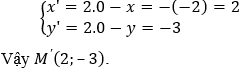
Câu 7. Trong mặt phẳng (Oxy), tìm ảnh của điểm A(5;3) qua phép đối xứng tâm I(4;1).
A. (5;3).
B. (-5;-3).
C. (3;-1).
D. (9/2;2).
Lời giải:
Chọn C
Gọi A' (x';y') là ảnh của A(5;3) qua phép đối xứng tâm I(4;1).
Ta có: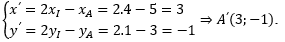 
Câu 8. Phép đối xứng tâm I(a;b) biến điểm A(1;3) thành điểm A'(1;7). Tính tổng T = a + b.
A. T = 4.
B. T = 6.
C. T = 7.
D. T = 8.
Lời giải:
.
Từ giả thiết, suy ra I là trung điểm của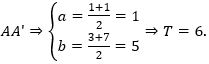 
Chọn B.
Câu 9. Phép đối xứng tâm O(0,0) biến điểm A(m;-m) thành điểm A' nằm trên đường thẳng x - y + 6=0. Tìm m.
A. m = 3.
B. m = 4.
C. m = -3.
D. m = -4.
Lời giải:
.
Ta có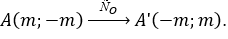 
Do A' nằm trên đường thẳng x - y + 6 = 0 nên -m - m + 6 = 0 ⇔ m = 3.
Chọn A.
Câu 10. Trong mặt phẳng tọa độ Oxy cho điểm M(2;1). Thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo vectơ 
= (1;2) biến điểm M thành điểm nào trong các điểm sau?
A. A(1;3).
B. B(2;0).
C. C(0;2).
D. D(-1;1).
Lời giải:
.
Phép đối xứng tâm O(0;0) biến điểm M(2;1) thành điểm M'(-2;-1).
Phép tịnh tiến theo vectơ = (1;2) biến điểm M'thành điểm M"
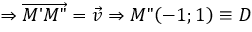
Chọn D.
Câu 11. Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng Δ: x + 2y - 3 = 0 và Δ': x - 2y - 7 = 0. Qua phép đối xứng tâm I(1;-3), điểm M trên đường thẳng Δ biến thành điểm N thuộc đường thẳng Δ'. Tính độ dài đoạn thẳng MN.
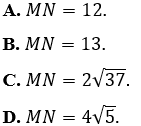
Lời giải:
.
Lấy điểm M(3-2m;m) thuộc Δ.
Gọi N là ảnh của M qua phép đối xứng tâm I(1;-3) → N(2m-1;-6-m).
Vì N ∈ Δ' nên (2m-1)-2(-6-m)-7=0 ⇔ m = -1.
Với m = -1 → M(5;-1), N(-3;-5)
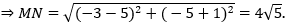
Chọn D.
