Cách tìm tâm đối xứng của một hình cực hay - Toán lớp 11
Cách tìm tâm đối xứng của một hình cực hay
Với Cách tìm tâm đối xứng của một hình cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm tâm đối xứng của một hình từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải
Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến hình H thành chính nó.
Khi đó ta nói H là hình có tâm đối xứng.
B. Ví dụ minh họa
Ví dụ 1: Tìm tâm đối xứng biến điểm A(1;3) thành điểm A'(1;7).
Hướng dẫn giải:
Từ giả thiết, suy ra I(a;b) là trung điểm của 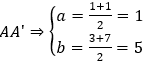
Vậy tâm đối xứng cần tìm là: I(1;5)
Ví dụ 2: Trong mặt phẳng Oxy cho đường thẳng d: x - 2y + 2 = 0 và d’: x - 2y - 8 = 0. Tìm phép đối xứng tâm biến d thành d’ và biến trục Ox thành chính nó.
Hướng dẫn giải:
Để thỏa mãn yêu cầu bài toán thì ta làm như sau:
- Gọi M(x;y) thuộc d, M’(x’;y’) thuộc d’. Giả sử tâm đối xứng là I(a;b), thì theo công thức chuyển trục:
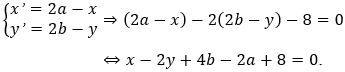
- Để trục Ox thành chính nó thì tâm đối xứng phải có dạng: I(a;0) tức là b = 0
- Từ hai kết quả trên ta có:
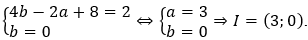
Ví dụ 3: Tìm tâm đối xứng của các hình sau
a) Hình tròn
b) Hình bình hành.
Hướng dẫn giải:
a)Tâm đối xứng của hình tròn là tâm của hình tròn đó.
b)Tâm đối xứng của hình hình bình hành là giao điểm của hai đường chéo.

C. Bài tập trắc nghiệm
Câu 1. Hình nào sau đây không có tâm đối xứng?
A. Hình vuông.
B. Hình tròn.
C. Hình tam giác đều.
D. Hình thoi.
Lời giải:
.
Chọn C.
(Hình vuông và hình thoi có tâm đối xứng là giao điểm của hai đường chéo).
Câu 2. Trong các hình sau đây, hình nào không có tâm đối xứng?
A. Hình gồm một đường tròn và một hình chữ nhật nội tiếp.
B. Hình gồm một đường tròn và một tam giác đều nội tiếp.
C. Hình lục giác đều.
D. Hình gồm một hình vuông và đường tròn nội tiếp.
Lời giải:
.
Chọn B.
Vì tam giác đều không có tâm đối xứng.
Câu 3. Trong các hình dưới đây hình nào không có tâm đối xứng ?
A. Đường elip.
B. Đường hypebol.
C. Đường parabol.
D. Đồ thị hàm số y=sinx.
Lời giải:
.
Chọn C.
Câu 4. Hình gồm hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng ?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Chọn B.
Có một tâm đối xứng chính là trung điểm của đoạn thẳng nối hai tâm của hai đường tròn.
Câu 5. Có bao nhiêu phép đối xứng tâm biến một đường thẳng a cho trước thành chính nó?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Chọn D.
Tâm đối xứng là điểm bất kỳ nằm trên đường thẳng a.
Câu 6. Cho hai đường thẳng song song d và d'. Có bao nhiêu phép đối xứng tâm biến mỗi đường thằng đó thành chính nó?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Tâm đối xứng phải nằm trên cả d và d' nên không có.
Chọn A.

Câu 7. Cho hai đường thẳng cắt nhau d và d'. Có bao nhiêu phép đối xứng tâm biến mỗi đường thẳng đó thành chính nó?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Chọn B.
Tâm đối xứng là giao điểm của d và d'.
Câu 8. Cho hai đường thẳng song song d và d'. Có bao nhiêu phép đối xứng tâm biến d thành d'?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Chọn D.
Tâm đối xứng là các điểm cách đều d và d'.
Câu 9. Cho bốn đường thẳng a, b, a', b' trong đó a||a', b||b' và a cắt b. Có bao nhiêu phép đối xứng tâm biến các đường thẳng a và b lần lượt thành các đường thẳng a' và b'?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
.
Chọn B.
Đó là phép đối xứng qua tâm hình bình hành tạo thành bởi bốn đường thẳng đã cho.
Câu 10. Hình nào sau đây vừa có tâm đối xứng, vừa có trục đối xứng?
A. Hình bình hành.
B. Hình bát giác đều.
C. Hình ngũ giác đều
D. Hình tam giác đều.
Lời giải:
.
Chọn B.
Câu 11. Hình nào sau đây có trục đối xứng nhưng không có tâm đối xứng?
A. Hình bình hành.
B. Hình bát giác đều.
C. Đường thẳng.
D. Hình tam giác đều.
Lời giải:
.
Chọn D.
Câu 12. Hình nào sau đây có tâm đối xứng (một hình là một chữ cái in hoa):
A. Q.
B. P.
C. N.
D. E.
Lời giải:
.
Chọn C.
Câu 13. Hình nào sau đây có trục đối xứng và đồng thời có tâm đối xứng?
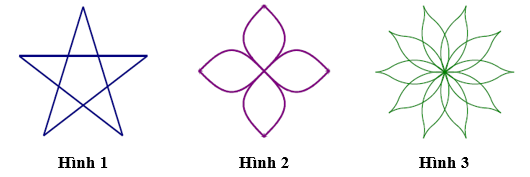
A. Hình 1 và Hình 2.
B. Hình 1 và Hình 3.
C. Hình 2 và Hình 3.
D. Hình 1, Hình 2 và Hình 3.
Lời giải:
.
Chọn C.
Câu 14. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Phép đối xứng tâm không có điểm nào biến thành chính nó.
B. Phép đối xứng tâm có đúng một điểm biến thành chính nó.
C. Có phép đối xứng tâm có hai điểm biến thành chính nó.
D. Có phép đối xứng tâm có vô số điểm biến thành chính nó.
Lời giải:
.
Chọn B.
Điểm đó là tâm đối xứng.

