Tìm ảnh của một đường thẳng qua phép vị tự cực hay - Toán lớp 11
Tìm ảnh của một đường thẳng qua phép vị tự cực hay
Với Tìm ảnh của một đường thẳng qua phép vị tự cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập ảnh của một đường thẳng qua phép vị tự từ đó đạt điểm cao trong bài thi môn Toán lớp 11.
A. Phương pháp giải
● Cách 1. Sử dụng tính chất: Phép vị tự biến một đường thẳng thành đường thẳng song song hoặc trùng với nói.
● Cách 2. Dùng biểu thức tọa độ của phép vị tự.
B. Ví dụ minh họa
Ví dụ 1: Trong mặt phẳng Oxy, cho đường thẳng d có phương trình 5x + 2y-7 = 0. Hãy viết phương trình của đường thẳng d' là ảnh của d qua phép vị tự tâm O tỉ số k = -2.
Hướng dẫn giải:
Cách 1: Lấy M(x;y) ∈ d ⇒ 5x + 2y - 7 = 0 (*).
Gọi M'(x';y') = V(O,-2)(M).
Theo biểu thức tọa độ ta có:
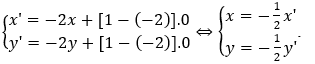
Thay vào (*) ta được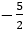 
x' - y' - 7 = 0 ⇔ 5x' + 2y' + 14 = 0
Vậy d': 5x + 2y + 14 = 0.
Cách 2: Do d' song song hoặc trùng với d nên phương trình có dạng : 5x + 2y+c = 0.
Lấy M(1;1) thuộc d. Gọi M'(x';y') = V(O,-2)(M) ta có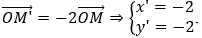 
Thay vào (*)ta được c = 14.
Vậy d': 5x + 2y + 14 = 0.
Ví dụ 2: Tìm ảnh của các đt d sau qua phép vị tự tâm O, tỉ số k, biết:
a) d: 4x – 3y + 1 = 0, k = -3
b) d: x – 4y + 2 = 0, k = 1/2
Hướng dẫn giải:
a)
* Cách 1: Gọi V(O,-3)(d) = d' ⇒ d’ // d nên PT đt d’ có dạng: 4x – 3y + C = 0
Chọn A(2; 3) ∈ d V(O,-3)(A) = A' (-6; -9) ∈ d’. Khi đó: -24 + 27 + C = 0 ⇔ C = -3
Vậy: PT đt d’ là: 4x – 2y – 3 = 0
* Cách 2: Chọn A(2; 3) ∈ d V(O,-3)(A) = A' (-6; -9) ∈ d’ và B(-1; -1) ∈ d V(O,-3)(B) = B' (3; 3) ∈ d’
PT đt d’ đi qua 2 điểm A’, B’ là:
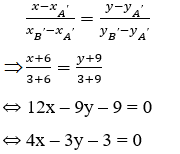
b)
* Cách 1: Gọi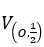 
(d) = d' ⇒ d’ // d nên PT đt d’ có dạng: x – 4y + C = 0
Chọn A(-2; 0) ∈ d 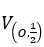(A) = A' (-1; 0) ∈ d’. Khi đó: -1 + C = 0 ⇔ C = 1
Vậy: PT đt d’ là: x – 4y + 1 = 0
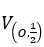
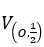
* Cách 2: Chọn A(-2; 0) ∈ d (A) = A' (-1; 0) ∈ d’ và B(6; 2) ∈ d (B) = B' (3; 1) ∈ d’
PT đt d’ đi qua 2 điểm A’, B’ là:
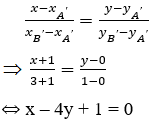
Ví dụ 3: Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d) có phương trình 2x + 3y - 1 = 0 và điểm I(-1;3), phép vị tự tâm I tỉ số k = -3 biến đường thẳng (d) thành đường thẳng (d'). Viết phương trình đường thẳng (d')
Hướng dẫn giải:
Chọn B
Đường thẳng (d') có dạng: 2x + 3y + m = 0.
Lấy A(-1;1) ∈ (d), gọi A'(x;y) là ảnh của A qua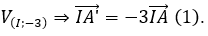 
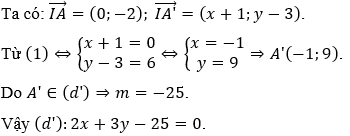
C. Bài tập trắc nghiệm
Câu 1. Trong mặt phẳng tọa độ Oxy cho đường thẳng d: 2x + y - 3 = 0. Phép vị tự tâm O, tỉ số k = 2 biến d thành đường thẳng nào trong các đường thẳng có phương trình sau?
A. 2x + y + 3 = 0.
B. 2x + y-6 = 0.
C. 4x - 2y - 3 = 0.
D. 4x + 2y - 5 = 0.
Lời giải:
.
Ta có V(O,2): d↦d' → d||d' nên d': 2x + y + c = 0 (c ≠ -3 do k ≠ 1).
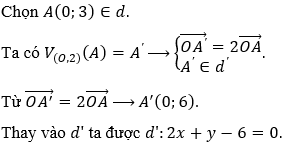
Chọn B.
Cách 2. Giả sử phép vị tự V(O,2) biến điểm M(x;y) thành điểm M'(x';y').
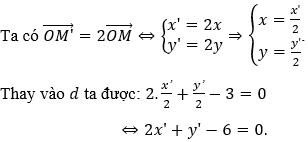
Câu 2. Trong mặt phẳng tọa độ Oxy cho đường thẳng Δ: x + 2y - 1 = 0 và điểm I(1;0). Phép vị tự tâm I tỉ số k biến đường thẳng Δ thành Δ' có phương trình là:
A. x - 2y + 3 = 0.
B. x + 2y - 1 = 0.
C. 2x - y + 1 = 0.
D. x + 2y + 3 = 0.
Lời giải:
.
Nhận xét. Mới đọc bài toán nghĩ rằng đề cho thiếu dữ kiện, cụ thể không cho k bằng bao nhiêu thì sao tìm được Δ'.
Để ý thấy I ∈ Δ do đó phép vị tự tâm I tỉ số k biến đường thẳng Δ thành Δ' trùng với Δ, với mọi k ≠ 0.
Chọn B.
Câu 3. Trong mặt phẳng tọa độ Oxy cho hai đường thẳng Δ1, Δ2 lần lượt có phương trình x - 2y + 1 = 0, x - 2y + 4 = 0 và điểm I(2;1). Phép vị tự tâm I tỉ số k biến đường thẳng Δ1 thành Δ2. Tìm k.
A. k = 1.
B. k = 2.
C. k = 3.
D. k = 4.
Lời giải:
.
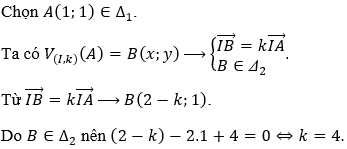
Chọn D.
Câu 4. Trong mặt phẳng tọa độ Oxy cho đường thẳng Δ: x + 2y - 1 = 0 và điểm I(1; 0). Phép vị tự tâm I tỉ số k biến đường thẳng Δ thành Δ' có phương trình là:
A. x - 2y + 3 = 0.
B. x + 2y - 1 = 0.
C. 2x - y + 1 = 0.
D. x + 2y + 3 = 0.
Lời giải:
Chọn B
Nhận xét. Mới đọc bài toán nghĩ rằng đề cho thiếu dữ kiện, cụ thể không cho k bằng bao nhiêu thì sao tìm được Δ'
Để ý thấy I ∈ Δ do đó phép vị tự tâm I tỉ số k biến đường thẳng Δ thành Δ' trùng với Δ, với mọi k ≠ 0.
Câu 5. Trong măt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Phép vị tự tâm O tỉ số k = -2 biến d thành đường thẳng nào trong các đường thẳng có phương trình sau?
A. 2x + 2y = 0.
B. 2x + 2y - 4 = 0.
C. x + y + 4 = 0.
D. x + y - 4 = 0.
Lời giải:
Chọn C
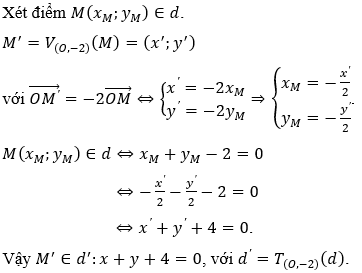
Câu 6. Cho phép biến hình F có quy tắc đặt ảnh tương ứng điểm M(x_M;y_M) có ảnh là điểm M'(x';y') theo công thức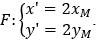 
. Viết phương trình đường thẳng d' là ảnh của đường thẳng d: x + 2y + 1 = 0 qua phép biến hình F.
A. d': 2x + y + 2 = 0.
B. d': x + 2y + 3 = 0.
C. d': x + 2y + 2 = 0.
D. d': x + 2y = 0.
Lời giải:
Chọn C
Cách 1:
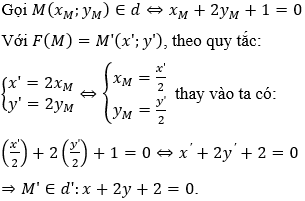
Cách 2: Chọn A-1;0) ∈ d, B(1;-1) ∈ d ⇒ F(A) = A'(-2;0) ∈ d', F(B) = B'(2;-2) ∈ d' ⇒ d'≡A'B'.
Đường thẳng d' qua A'(-2;0) và nhận vecto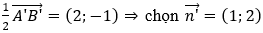 
làm 1 vecto pháp tuyến, suy ra d': 1(x + 2) + 2(y - 0) = 0 ⇔ x + 2y + 2 = 0
Câu 7. Trong măt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Phép vị tự tâm O tỉ số k = -2 biến d thành đường thẳng nào trong các đường thẳng có phương trình sau?
A. 2x + 2y = 0.
B. 2x + 2y - 4 = 0.
C. x + y + 4 = 0.
D. x + y - 4 = 0.
Lời giải:
Chọn C
V(O,k)(d) = d' ⇒ d': x + y + c = 0.
Ta có: M(1;1) ∈ d và V(O,k)(M) = M' ⇒ M'(-2;-2) ∈ d'.
Từ và ta có: c = 4.
Câu 8. Cho hai đường thẳng cắt nhau d và d'. Có bao nhiêu phép vị tự biến d thành đường thằng d'?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
Chọn A
Vì qua phép vị tự, đường thẳng biến thành đường thẳng song song hoặc trùng với nó.
Câu 9. Cho hai đường thẳng song song d và d'. Có bao nhiêu phép vị tự với tỉ số k = 20 biến đường thẳng d thành đường thẳng d'?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
Chọn D
Lấy hai điểm A và A' tùy ý trên d và d'. Chọn điểm O thỏa mãn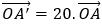 
. Khi đó phép vị tự tâm O tỉ số k = 20 sẽ biến d thành đường thẳng d'.
Do A và A' tùy ý trên d và d' nên suy ra có vô số phép vị tự.
Câu 10. Cho hai đường thẳng song song d và d' và một điểm O không nằm trên chúng. Có bao nhiêu phép vị tự tâm O biến đường thẳng d thành đường thằng d'?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
Chọn B
Kẻ đường thẳng Δ qua O, cắt d tại A và cắt d' tại A'.
Gọi k là số thỏa mãn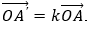 
Khi đó phép vị tự tâm O tỉ số k sẽ biến d thành đường thẳng d'.
Do k xác định duy nhất nên có duy nhất một phép vị tự.
Câu 11. Cho hai đường thẳng cắt nhau d và d'. Có bao nhiêu phép vị tự biến mỗi đường thẳng thành chính nó ?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải:
Chọn D
Tâm vị tự là giao điểm của d và d'. Tỉ số vị tự là số k khác 0.
