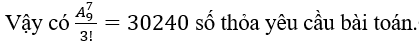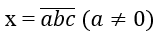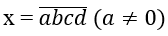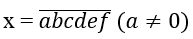Trắc nghiệm bài toán đếm số tự nhiên - Toán lớp 11
Trắc nghiệm bài toán đếm số tự nhiên
Với Trắc nghiệm bài toán đếm số tự nhiên Toán lớp 11 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập bài toán đếm số tự nhiên từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

Bài 1: Xếp 6 người A, B, C, D, E, F vào một ghế dài.Hỏi có bao nhiêu cách sắp xếp sao cho: A và F ngồi cạnh nhau
A. 242 B. 240 C. 244 D. 248
Lời giải:
Đáp án: B
Xem AF là một phần tử X, ta có: 5! = 120 số cách xếp X,B,C,D, E. Khi hoán vị A,F ta có thêm được một cách xếp
Vậy có 240 cách xếp thỏa yêu cầu bài toán. Chọn B.
Bài 2: Xếp 6 người A, B, C, D, E, F vào một ghế dài.Hỏi có bao nhiêu cách sắp xếp sao cho: A và F không ngồi cạnh nhau
A. 480 B. 460 C. 246 D. 260
Lời giải:
Đáp án: A
Ta có: 6! = 720 số cách xếp A,B,C,D, E,F. Dựa vào bài 1 số cách để A và F ngồi cạnh nhau là 240. Vậy số cách để A, F không ngồi cạnh nhau là: 720 – 240 = 480 cách. Chọn A.
Bài 3: Có bao nhiêu cách xếp n người ngồi vào một bàn tròn.
A. n! B. (n – 1)! C. 2(n – 1)! D. (n – 2)!
Lời giải:
Đáp án: B
Nếu xếp một người ngồi vào một vị trí nào đó thì ta có 1 cách xếp và n – 1 người còn lại được xếp vào n - 1 vị trí còn lại nên có (n – 1)! cách xếp.
Vậy có tất cả (n – 1)! cách xếp. Chọn B.
Bài 4: Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là:

Lời giải:
Đáp án: A
Số tập con có 3 phần tử của một tập hợp có 7 phần tử là số tổ hợp chập 3 của 7. Vậy chọn A.
Bài 5: Cho các số 1,2,4,5,7 có bao nhiêu cách tạo ra một số chẵn gồm 3 chữ số khác nhau từ 5 chữ số đã cho:
A. 120. B.256. C.24. D.36.
Lời giải:
Đáp án: C
Gọi số cần tìm có dạng :
Chọn c có 2 cách chọn (c ∈ {4,2} ).


Bài 6: Từ các số 1, 2, 3, 4, 5, 6 lập được bao nhiêu số tự nhiên?
Gồm 4 chữ số
A. 1296 B. 2019 C. 2110 D. 1297
Lời giải:
Đáp án: A
Gọi số cần lập là:
Ta chọn a,b,c,d theo thứ tự sau
a: có 6 cách chọn
b:có 6 cách chọn
c: có 6 cách chọn
d: có 6 cách chọn
Vậy có 64 = 1296 số. Chọn A
Bài 7: Từ các số 1, 2, 3, 4, 5, 6 lập được bao nhiêu số tự nhiên?
Gồm 3 chữ số đôi một khác nhau
A. 110 B. 121 C. 120 D. 125
Lời giải:
Đáp án: C
Mỗi số cần lập ứng với một chỉnh hợp chập 3 của 6 phần tử
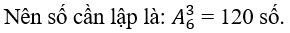
Bài 8: Từ các số 1, 2, 3, 4, 5, 6 lập được bao nhiêu số tự nhiên?
Gồm 4 chữ số đôi một khác nhau và là chữ số tự nhiên chẵn
A. 182 B. 180 C. 190 D. 192
Lời giải:
Đáp án: B
Gọi số cần lập là:
Vì x chẵn nên chọn d có 3 cách chọn.

Bài 9: Từ các số 1, 2, 3, 4, 5, 6 lập được bao nhiêu số tự nhiên?
Gồm 4 chữ số đôi một khác nhau và không bắt đầu bằng chữ số 1
A. 300 B. 320 C. 310 D. 330
Lời giải:
Đáp án: A
Gọi số cần lập là:
Vì a ≠ 1 nên chọn a có 5 cách chọn.

Bài 10: Từ các số 1, 2, 3, 4, 5, 6 lập được bao nhiêu số tự nhiên?
Gồm 6 chữ số đôi một khác nhau và hai chữ số 1 và 2 không đứng cạnh nhau.
A. 410 B. 480 C. 500 D. 512
Lời giải:
Đáp án: B
Ta tính số trường hợp để 1 và 2 đứng cạnh nhau:
Đặt y = 12, xét các số 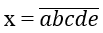
Số cách chọn một số thỏa mãn điều kiện trên là một hoán vị của 5 phần. Vậy có P5 số.
Khi ta hoán vị 2,1 trong y ta được hai số khác nhau
Nên có P5.2 = 240 số.
Số các số lập được từ 6 số trên là 6!.
Số các số thỏa mãn điều kiện đề bài cho là 6! – 240 =480. Chọn B

Bài 11: Từ 7 chữ số 1,2,3,4,5,6,7 có thể lập được bao nhiêu số từ 4 chữ số khác nhau?
A. 7!. B. 74. C. 7.6.5.4. D.7!.6!.5!.4!.
Lời giải:
Đáp án: C
Gọi số cần lập là:
Ta chọn a,b,c,d theo thứ tự sau
a: có 7 cách chọn
b: có 6 cách chọn
c: có 5 cách chọn
d: có 4 cách chọn
Vậy có 7.6.5.4 số. Chọn C.
Bài 12: Cho tập A = {1,2,3,4,5,6,7,8}. Có bao nhiêu tập con của A chứa số 2 mà không chứa số 3
A. 64 B. 83 C. 13 D. 41
Lời giải:
Đáp án: B
Xét tập B = {1,4,5,6,7,8}, ta có B không chứa số 3.
X là một tập con của A thỏa yêu cầu bài toán khi và chỉ khi X\{2} là một tập con của B. Do đo, số tập con của A thỏa yêu cầu bài toán bằng số tập con của B và bằng 26 = 64. Chọn A.
Bài 13: Từ các số của tập A = {1,2,3,4,5,6,7} lập được bao nhiêu số tự nhiên gồm
Năm chữ số đôi một khác nhau
A. 2520 B. 2510 C. 2398 D. 2096
Lời giải:
Đáp án: A
. Mỗi số cần lập thỏa yêu cầu bài toán sẽ ứng với mỗi chỉnh hợp chập 5 của 7 phần tử.
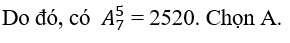
Bài 14: Từ các số của tập A = {1,2,3,4,5,6,7} lập được bao nhiêu số tự nhiên gồm
Sáu chữ số khác nhau và chia hết cho 5.
A. 720 B. 710 C. 820 D. 280
Lời giải:
Đáp án: A
Gọi số cần lập là
Vì x chia hết cho 5 nên f = 5 . Vậy f có một cách chọn
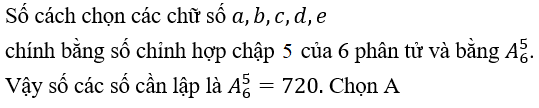
Bài 15: Từ các số của tập A = {1,2,3,4,5,6,7} lập được bao nhiêu số tự nhiên gồm
Bảy chữ số, trong đó chữ số 2 xuất hiện đúng ba lần.
A. 31203 B. 30240 C. 31220 D. 32220
Lời giải:
Đáp án: B
Xét các số tự nhiên có bảy chữ số được lập từ {1,2,2,2,3,4,5,6,7}
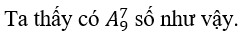
Tuy nhiên khi hoán vị vị trí của ba số 2 cho nhau thì số thu được không thay đổi.