Cách giải Bài toán tổ hợp trong hình học cực hay - Toán lớp 11
Cách giải Bài toán tổ hợp trong hình học cực hay
Với Cách giải Bài toán tổ hợp trong hình học cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tổ hợp trong hình học từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải & Ví dụ
Dựa vào hai quy tắc cộng, quy tắc nhân và các khái niệm hoán vị, chỉnh hợp, tổ hợp, đếm gián tiếp, đếm phần bù.
Một số dấu hiệu giúp chúng ta nhận biết được hoán vị, chỉnh hợp hay tổ hợp.
1) Hoán vị: Các dấu hiệu đặc trưng để giúp ta nhận dạng một hoán vị của n phần tử là:
♦ Tất cả n phần tử đều phải có mặt
♦ Mỗi phần tử xuất hiện một lần.
♦ Có thứ tự giữa các phần tử.
2) Chỉnh hợp: Ta sẽ sử dụng khái niệm chỉnh hợp khi
♦ Cần chọn k phần tử từ n phần tử, mỗi phần tử xuất hiện một lần
♦ k phần tử đã cho được sắp xếp thứ tự.
3) Tổ hợp: Ta sử dụng khái niệm tổ hợp khi
♦ Cần chọn k phần tử từ n phần tử, mỗi phần tử xuất hiện một lần
♦ Không quan tâm đến thứ tự k phần tử đã chọn.
Ví dụ minh họa
Bài 1: Cho hai đường thẳng song song d1, d2. Trên đường thẳng d1 lấy 10 điểm phân biệt, trên d2 lấy 15 điểm phân biệt. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 25 vừa nói trên.
Số tam giác lập được thuộc vào một trong hai loại sau
Bài 2: Số tam giác xác định bởi các đỉnh của một đa giác đều 10 cạnh là:


B. Bài tập vận dụng
Bài 1: Nếu tất cả các đường chéo của đa giác đều 12 cạnh được vẽ thì số đường chéo của đa giác đó là bao nhiêu?
Lời giải:
Cứ 2 đỉnh của đa giác sẽ tạo thành một đoạn thẳng (bao gồm cả cạnh đa giác và đường chéo).
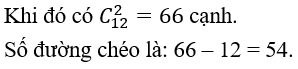
Bài 2: Nếu một đa giác đều có 44 đường chéo, thì số cạnh của đa giác đó là bao nhiêu?
Lời giải:
Cứ hai đỉnh của đa giác n (n ∈ N, n ≥ 3) đỉnh tạo thành một đoạn thẳng (bao gồn cả cạnh đa giác và đường chéo).
Khi đó số đường chéo là:
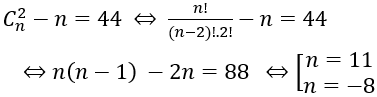
Vậy số cạnh của đa giác đó là 11.
Bài 3: Một đa giác đều có số đường chéo gấp đôi số cạnh. Hỏi đa giác đó có bao nhiêu cạnh?
Lời giải:
Đa giác có n (n ∈ N, n ≥ 3).

Vậy số cạnh của đa giác đó là 7.
Bài 4: Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt (n ≥ 2). Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?
Lời giải:
Tam giác cần lập thuộc hai loại

Theo bài ra ta có:
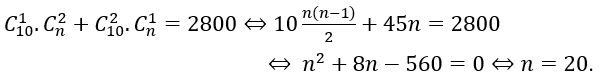
Bài 5: Cho hai đường thẳng song song d1, d2. Trên đường thẳng d1 lấy 10 điểm phân biệt, trên d2 lấy 5 điểm phân biệt. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 25 vừa nói trên.
Lời giải:
Số tam giác lập được thuộc vào một trong hai loại sau





