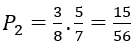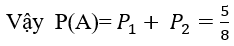Trắc nghiệm các quy tắc tính xác suất - Toán lớp 11
Trắc nghiệm các quy tắc tính xác suất
Với Trắc nghiệm các quy tắc tính xác suất Toán lớp 11 tổng hợp 10 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập quy tắc tính xác suất từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

Bài 1: Gieo hai con súc sắc. Xác suất để tổng số chấm trên hai mặt chia hết cho 3 là:
A.13/36 B. 11/36. C. 1/3. D. 1/6.
Lời giải:
Đáp án: C
Chọn C.
Số phần tử không gian mẫu:n(Ω)=6.6=36
Biến cố tổng hai mặt chia hết cho 3 là:
A={(1,2);(1,5);(2,1);(2,4);(3,3);(3,6);(4,2);(4,5);(5,1);(5,4);(6,3);(6,6)}
Nên n(A)=12
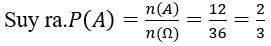
Bài 2: Gieo ba con súc sắc. Xác suất để nhiều nhất hai mặt 5 là:
A. 5/72. B. 1/216 C. 1/72. D.0
Lời giải:
Đáp án: D
Chọn D.
Số phần tử không gian mẫu: n(Ω)=6.6.6=216
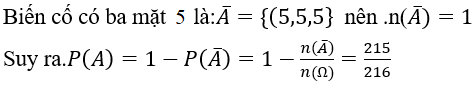
Bài 3: Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá át (A) là:
A. 2/13. B. 1/169. C. 1/13. D. 3/4 .
Lời giải:
Đáp án: C
Chọn C.
Số phần tử không gian mẫu: : n(Ω)=52
Số phần tử của biến cố xuất hiện lá ách: : n(A)=4
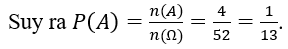
Bài 4: Rút ra một lá bài từ bộ bài lá. Xác suất để được lá ách (A) hay lá rô là:
A. 1/52. B. 2/13. C. 4/13. D. 17/52.
Lời giải:
Đáp án: C
Chọn C.
Số phần tử không gian mẫu: : n(Ω)=52
Số phần tử của biến cố xuất hiện lá ách : n(A)=4
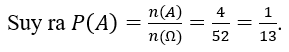
Bài 5: Một túi chứa 2 bi trắng và 3 bi đen. Rút ra 3 bi. Xác suất để được ít nhất 1 bi trắng là:
A. 1/5. B. 1/10. C. 9/10. D. 4/5.
Lời giải:
Đáp án: C
Số phần tử của không gian mẫu: n(Ω)=10
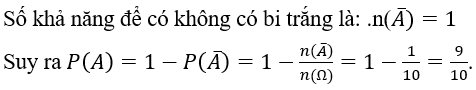

Bài 6: Một hộp đựng 4 bi xanh và bi đỏ lần lượt rút 2 viên bi. Xác suất để rút được một bi xanh và 1 bi đỏ là:
A. 2/15. B. 6/25. C. 8/25. D. 4/15.
Lời giải:
Đáp án: D
Phép thử : Rút lần lượt hai viên bi
Ta có n(Ω)=9.10=90
Biến cố A : Rút được một bi xanh, một bi đỏ n(Ω)=4.6=24
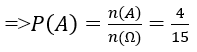
Bài 7: Một bình đựng 4 quả cầu xanh và 3 quả cầu đỏ và quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Xác suất để được 3 quả cầu khác màu là:
A. 3/5. B. 3/7. C. 3/11. D. 3/14.
Lời giải:
Đáp án: C
Phép thử : Rút ngẫu nhiên ba quả cầu
Ta có n(Ω)=220
Biến cố A : Rút được ba qua cầu khác màu n(A)=5.4.3=60
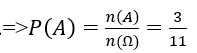
Bài 8: Một bình đựng viên bi xanh và viên bi đỏ (các viên bi chỉ khác nhau về màu sắc). Lấy ngẫu nhiên một viên bi, rồi lấy ngẫu nhiên một viên bi nữa. Khi tính xác suất của biến cố "Lấy lần thứ hai được một viên bi xanh", ta được kết quả
A. 5/8 B. 5/9 C. 5/7 D. 4/7
Lời giải:
Đáp án: A
Chọn A.
Gọi A là biến cố "Lấy lần thứ hai được một viên bi xanh". Có hai trường hợp xảy ra
Trường hợp 1. Lấy lần thứ nhất được bi xanh, lấy lần thứ hai cũng được một bi xanh. Xác suất trong trường hợp này là
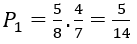
Trường hợp 2. Lấy lần thứ nhất được bi đỏ, lấy lần thứ hai được bi xanh. Xác suất trong trường hợp này là
Bài 9: Một hộp có 5 viên bi đỏ và 9 viên bi xanh. Chọn ngẫu nhiên 2 viên bi. Xác suất để chọn được 2 viên bi khác màu là:
A. 14/35. B. 45/91. C. 46/91. D. 15/22.
Lời giải:
Đáp án: B
Chọn B.
Gọi A là biến cố: "chọn được 2 viên bi khác màu."
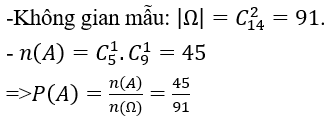
Bài 10: Một hộp chứa ba quả cầu trắng và hai quả cầu đen. Lấy ngẫu nhiên đồng thời hai quả. Xác suất để lấy được cả hai quả trắng là:
A. 2/10 B. 3/10 C. 4/10 D. 5/10
Lời giải:
Đáp án: B
Chọn B.
Gọi A là biến cố: "lấy được cả hai quả trắng."