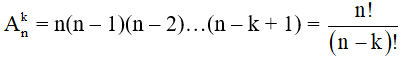Cách giải bài tập qui tắc hoán vị, chỉnh hợp, tổ hợp cực hay, chi tiết - Toán lớp 11

---

Cách giải bài tập qui tắc hoán vị, chỉnh hợp, tổ hợp cực hay, chi tiết

Với Cách giải bài tập qui tắc hoán vị, chỉnh hợp, tổ hợp cực hay, chi tiết Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập qui tắc hoán vị, chỉnh hợp, tổ hợp từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

I. Hoán vị

a) Định nghĩa hoán vị:

Một tập hợp gồm n phần tử (n 1). Mỗi cách sắp xếp n phần tử này theo một thứ tự nào đó được gọi là một hoán vị của n phần tử.

b) Số các hoán vị:

    P_n = n! = n(n – 1)(n – 2) … 1.

c) Hoán vị vòng quanh

Cho tập A gồm n phần tử. Một cách sắp xếp n phần tử của tập A thành một dãy kín được gọi là một hoán vị vòng quanh của n phần tử.

Số các hoán vị vòng quanh của n phần tử: Q_n = (n – 1)!

d) Ví dụ minh họa

Ví dụ 1. Lớp 11K có 10 học sinh. Ta muốn sắp xếp thành một hàng ngang thì có bao nhiêu cách xếp?

Hướng dẫn

Mỗi cách xếp 10 học sinh của lớp 11K thành một hàng ngang là một hoán vị của 10.

Vậy ta có tất cả: P₁₀ = 10! = 3628800 cách xếp.

Ví dụ 2. Lớp 11K có 10 học sinh. Ta muốn sắp xếp thành một vòng tròn thì có bao nhiêu cách xếp?

Hướng dẫn

Mỗi cách xếp 10 học sinh của lớp 11K thành một vòng tròn kín được gọi là một hoán vị vòng quanh của 10.

Vậy ta có tất cả: Q₁₀ = (10 – 1)! = 9! = 362880 cách xếp.

Ví dụ 3. Trong tủ sách có tất cả 5 quyển sách khác nhau. Hỏi có bao nhiêu cách xếp sao cho quyển sách thứ nhất kề quyển sách thứ hai.

Hướng dẫn

+ Chọn hai vị trí liên tiếp trong 5 vị trí gộp lại để xếp quyển thứ nhất và quyển thứ hai kề nhau. Suy ra có 4 vị trí để xếp hai quyển này, vậy có 4 cách.

+ Xếp hai quyển sách thứ nhất và thứ hai, có hai cách xếp (hoán vị cho nhau)

+ Sắp 3 quyển sách còn lại vào 3 vị trí, có 3! cách.

+ Vậy có tất cả: 4. 2. 3! = 8. 6 = 48 cách.

II. Chỉnh hợp

a) Định nghĩa

Cho tập hợp A gồm n phần tử. Mỗi cách sắp xếp k phần tử của A (1 ≤ k ≤ n) theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử của tập A.

b) Số các chỉnh hợp chập k của n phần tử

Chú ý:

- Công thức trên cũng đúng cho trường hợp k = 0 và k = n

Quy ước: 0! = 1 và A_n⁰ = 1

- Khi k = n thì A_nⁿ = P_n = n! (hoán vị)

Ví dụ minh họa

Ví dụ 1. Xếp 5 người vào mỗi băng ghế có 7 chỗ. Hỏi có bao nhiêu cách xếp? (mỗi người ngồi một ghế).

Hướng dẫn

+ Mỗi cách chọn ra 5 chỗ ngồi từ băng ghế 7 chỗ ngồi và xếp 5 người đó vào 5 vị trí ngồi chính là chỉnh hợp chập 5 của 7.

+ Vậy có: A₇⁵ = 2520 cách.

Ví dụ 2. Trong mặt phẳng, cho một tập gồm 7 điểm phân biệt. Có bao nhiêu vecto khác vecto 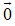có điểm đầu và điểm cuối thuộc tập hợp điểm này?

Hướng dẫn

+ Mỗi cặp sắp thứ tự gồm hai điểm (A, B) cho ta một vecto có điểm đầu là A, điểm cuối là B và ngược lại. Như vậy, mỗi vecto có thể xem là một chỉnh hợp chập 2 của tập hợp 7 điểm đã cho.

+ Vậy số vecto cần tìm là: A₇² = 42 (vecto).

III. Tổ hợp

a) Định nghĩa

Cho tập A gồm n phần tử. Mỗi tập con gồm k (1 ≤ k ≤ n) phần tử của A được gọi là một tổ hợp chập k của n phần tử.

b) Số các tổ hợp chập k của n phần tử

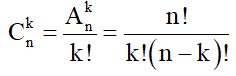
Lưu ý: Công thức này cũng đúng với k = 0

Quy ước: C_n⁰ = 1 (coi ∅ là tổ hợp chập 0 của tập hợp có n phần tử)

c) Ví dụ minh họa

Ví dụ 1. Có 10 cuốn sách khác nhau. Chọn ra 4 cuốn sách. Hỏi có bao nhiêu cách chọn.

Hướng dẫn

Mỗi cách chọn ra 4 cuốn sách trong 10 cuốn sách là một tổ hợp chập 4 của 10.

Vậy có C₁₀⁴ = 210 cách chọn.

Ví dụ 2. Lớp 11A có 19 học sinh nam và 15 học sinh nữ. Giáo viên chủ nhiệm cần chọn ra 4 bạn nam và 2 bạn nữ để đi tham gia chiến dịch phòng chống “Sốt xuất huyết” của Huyện Đoàn. Hỏi có bao nhiêu cách chọn.

Hướng dẫn

+ Chọn ra 4 bạn nam trong 19 bạn nam có: C₁₉⁴= 3876 cách chọn

+ Chọn ra 2 bạn nữ trong 15 bạn nữ có: C₁₅² = 105 cách chọn

+ Theo quy tắc nhân, số cách chọn là: 3876 . 105 = 406980 cách.

IV. Phân biệt hoán vị, chỉnh hợp và tổ hợp

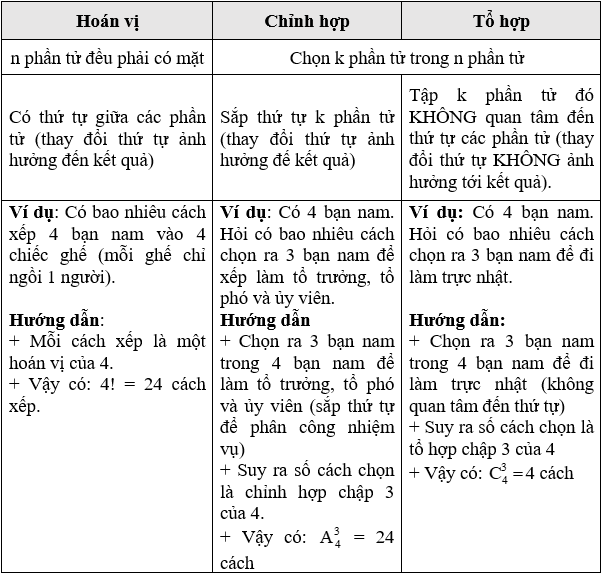
V. Các dạng toán thường gặp sử dụng kết hợp hoán vị, chỉnh hợp, tổ hợp

a) Dạng 1: Bài toán đếm

● Phương pháp giải:

Sử dụng hai quy tắc công và quy tắc nhân, các khái niệm hoán vị, chỉnh hợp và tổ hợp.

● Ví dụ minh họa

Ví dụ 1. Từ 7 chữ số 1, 2, 3, 4, 5, 6, 7, có thể lập được bao nhiêu số tự nhiên có 4 chữ số khác nhau gồm 2 chữ số chẵn và 2 chữ số lẻ?

A. 840

B. 432

C. 35

D. 576

Hướng dẫn

+ Các chữ số lẻ trong 7 chữ số trên là: 1, 3, 5, 7, có 4 số

Suy ra chọn hai chữ số lẻ có: C₄² cách

+ Các chữ số chẵn trong 7 chữ số trên là: 2, 4, 6, có 3 số

Suy ra chọn hai chữ số chẵn: có C₃² cách

+ Với 4 chữ số đã chọn ở trên, ta xếp vào 4 vị trí có: 4! cách

Theo quy tắc nhân, vậy có thể lập được: C₄².C₃².4! = 432 số.

Đáp án B

Ví dụ 2. Từ các chữ số của tập hợp {0; 1; 2; 3; 4; 5}, có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi mội khác nhau mà trong đó nhất thiết phải có mặt chữ số 0?

A. 120

B. 504

C. 720

D. 480

Hướng dẫn

Giả sử số tự nhiên có 5 chữ số có dạng: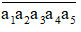

+ Ta có: a₁ ∈ {1;2;3;4;5} (vì chữ số đầu tiên không thể bằng 0) ⇒ Có 5 cách chọn a₁

+ Tiếp theo ta bỏ a1 và 0 thì tập hợp đã cho còn lại 4 chữ số. Ta chọn 3 chữ số từ 4 chữ số đó, ta có C₄³ cách chọn.

Chúng ta xếp chữ số 0 và 3 chữ số vừa chọn được vào 4 vị trí a₂; a₃; a₄; a₅ ta được 4! cách xếp.

Do đó chọn cho các chữ số a₂; a₃; a₄; a₅ có mặt chữ số 0 ta có: C₄³.4! cách.

+ Vậy theo quy tắc nhân, số số tự nhiên thỏa mãn yêu cầu đề bài có thể lập được là: 5.C₄³.4! = 480 số.

Đáp án D

Ví dụ 3. Một nhóm 6 bạn học sinh mua vé vào rạp chiếu phim. Các bạn mua 6 vé gồm 3 vé mang ghế số chẵn, 3 vé mang ghế số lẻ và không có hai vé nào cùng số. Trong 6 bạn thì hai bạn muốn ngồi bên ghế chẵn, hai bạn muốn ngồi bên ghế lẻ, hai bạn còn lại không có yêu cầu gì. Hỏi có bao nhiêu cách xếp chỗ để thỏa mãn yêu cầu của tất cả các bạn đó?

A. 36

B. 180

C. 72

D. 18

Hướng dẫn

+ Trong 6 vé có 3 vé mang ghế số chẵn, do đó xếp 2 bạn vào ghế mang số chẵn có A₃²cách (vì sắp thứ tự luôn hai bạn đó nên ta dùng chỉnh hợp).

+ Tương tự, xếp hai bạn vào ghế mang số lẻ có A₃² cách.

+ Vậy còn lại 2 bạn và 2 chỗ, Số cách xếp hai bạn còn lại vào hai vị trí còn lại là 2! cách.

+ Theo quy tắc nhân, vậy số cách xếp thỏa mãn yêu cầu của tất cả các bạn đó là: A₃².A₃².2! = 72 cách.

Đáp án C

b) Dạng 2: Bài toán chọn người (vật), xếp vị trí, công việc

● Phương pháp giải

Sử dụng các quy tắc cộng, quy tắc nhân, khái niêm hoán vị, chỉnh hợp và tổ hợp.

● Ví dụ minh họa

Ví dụ 1. Có 5 tem thư khác nhau và 6 bì thư cũng khác nhau. Người ta muốn chọn 3 tem thư, 3 bì thư và dán 3 tem thư ấy lên 3 bì thư đã chọn, mỗi bì thư chỉ dán một tem thư. Hỏi có bao nhiêu cách làm như vậy?

A. 1200

B. 1800

C. 1000

D. 200

Hướng dẫn

+ Chọn 3 bì thư trong 6 bì thư có C₆³ cách.

+ Chọn 3 tem thư trong 5 tem thư có C₅³ cách.

+ Dán 3 tem thư lên 3 bì thư thì có 3! cách dán.

+ Theo quy tắc nhân, vậy số cách chọn cần tìm là: C₆³.C₅³.3! = 1200 cách.

Đáp án A

Ví dụ 2. Có 2 học sinh lớp A, 3 học sinh lớp B và 4 học sinh lớp C xếp thành một hàng ngang sao cho giữa hai học sinh lớp A không có học sinh nào lớp B. Hỏi có bao nhiêu cách xếp hàng như vậy?

A. 80640

B. 108864

C. 145152

D. 217728

Hướng dẫn

Xét các trường hợp sau:

+ TH1: Hai học sinh lớp A đứng cạnh nhau

Gộp 2 học sinh lớp A lại thành một (để đứng cạnh nhau) và xếp cùng với 7 học sinh của hai lớp còn lại thì có 8! cách.

Xếp hai học sinh lớp A thì có 2! cách.

Vậy có: 2!.8! cách xếp để 2 học sinh lớp A đứng cạnh nhau.

+ TH2: Giữa hai học sinh lớp A có 1 học sinh lớp C.

Chọn 1 học sinh lớp C để xếp cùng 2 học sinh lớp A có A₄¹ cách.

Xếp hai học sinh lớp A thì có 2! cách.

Xếp 6 học sinh còn lại của hai lớp cùng với 1 nhóm 3 học sinh trên có 7! cách

Vậy có: 2!. A₄¹.7! cách xếp để có 1 học sinh lớp C đứng giữa hai học sinh lớp A.

+ TH3: Giữa hai học sinh lớp A có 2 học sinh lớp C.

Tương tự TH2, vậy ta có: 2!. A₄². 6! cách.

+ TH4: Giữa hai học sinh lớp A có 3 học sinh lớp C, có 2!.A₄³.5! cách.

+ TH5: Giữa hai học sinh lớp A có 4 học sinh lớp C, có 2!.A₄⁴.4! cách.

Vậy theo quy tắc cộng ta có:

 2!.8! + 2!. A₄¹.7! + 2!. A₄².6! + 2!. A₄³.5! + 2!.A₄⁴.4! = 145152 cách.

Đáp án C

Ví dụ 3. Ông và bà An cùng 6 đứa con đang lên máy bay theo một hàng dọc. Có bao nhiêu cách xếp hàng khác nhau nếu ông An hay bà An đứng ở đầu hàng hoặc cuối hàng.

A. 720

B. 1440

C. 18720

D. 40320

Hướng dẫn

Bài này ta dùng phần bù để giải quyết.

+ Có tất cả 8 người cùng lên máy bay, xếp 8 người thành một hàng dọc có 8! cách.

+ Xếp ông An và bà An vào 2 trong 6 vị trí ở giữa (8 vị trí trừ đi 2 vị trí ở đầu và cuối hàng) thì có A₆² cách.

Xếp 6 người con vào 6 vị trí còn lại có 6! cách.

Do đó số cách xếp để ông An và bà An không đứng ở vị trí đầu và cuối hàng là A₆².6! cách.

+ Vậy số cách xếp để ông An hay bà An đứng ở vị trí đầu hoặc cuối hàng là

    8! - A₆².6! = 10720 cách.

Đáp án C

c) Dạng 3: Bài toán liên quan đến hình học

● Phương pháp giải

- Sử dụng các quy tắc nhân, quy tắc cộng và các khái niệm hoán vị, chỉnh hợp và tổ hợp.

- Vận dụng các khái niệm hình học liên quan.

● Ví dụ minh họa

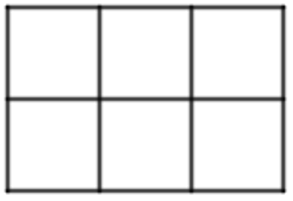
Ví dụ 1. Bé Minh có một bảng hình chữ nhật gồm 6 hình vuông đơn vị, cố định không xoay như hình vẽ dưới. Bé muốn dùng 3 màu để tô tất cả các cạnh của các hình vuông đơn vị, mỗi cạnh tô một lần sao cho mỗi hình vuông đơn vị được tô bởi đúng 2 màu, trong đó mỗi màu tô đúng 2 cạnh. Hỏi bé Minh có tất cả bao nhiêu cách tô màu bảng?

A. 4374

B. 139968

C. 576

D. 15552

Hướng dẫn

Tô màu theo nguyên tắc sau:

+ Tô 1 ô vuông 4 cạnh: Chọn 2 trong 3 màu, ứng với 2 màu được chọn có 6 cách tô. Do đó có 6.C₃² cách tô.

+ Tô 3 ô vuông 3 cạnh (có một cạnh đã được tô trước đó): ứng với một ô vuông có 3 cách tô màu 1 trong 3 cạnh theo màu của cạnh đã tô trước đó, chọn 1 trong hai màu còn lại tô hai cạnh còn lại, có 3. C₂¹ = 6 cách tô. Do đó có 6³ cách tô.

+ Tô 2 ô vuông 2 cạnh (có 2 cạnh đã được tô trước đó): ứng với mỗi ô vuông có 2 cách tô màu 2 cạnh ( 2 cạnh tô trước cùng màu hay khác màu nhau không ảnh hưởng đến số cách tô). Do đó có 2² cách tô.

+ Vậy có: 6. C₃².6³.2² = 15552 cách tô.

Đáp án D

d) Dạng 4: Giải phương trình, bất phương trình, hệ phương trình liên quan hoán vị, chỉnh hợp và tổ hợp.

● Phương pháp giải

- Dựa vào công thức hoán vị, chỉnh hợp, tổ hợp và một số tính chất của nó để chuyển phương trình, bất phương trình, hệ tổ hợp về dạng phương trình, bất phương trình, hệ phương trình đại số để giải.

- Một số công thức hoán vị, chỉnh hợp, tổ hợp và tính chất

Cho n là số nguyên dương và 0 ≤ k ≤ n, ta có:

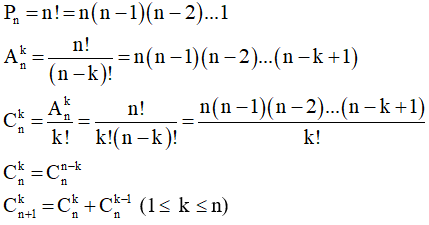
- Chú ý về điều kiện của phương trình, bất phương trình và hệ.

● Ví dụ minh họa

Ví dụ 1. Số các số nguyên dương n thỏa mãn 6n – 6 + C_n³ = C_{n + 1}³ là

A. 0

B. 1

C. 2

D. Vô số

Hướng dẫn

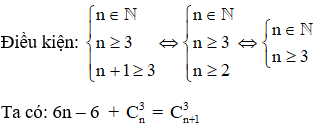
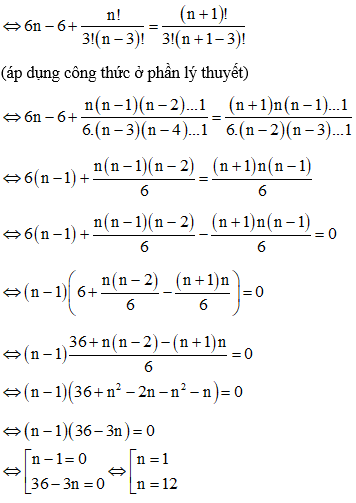
Đối chiếu điều kiện vậy n = 12

Vậy có 1 số nguyên dương n thỏa mãn bài toán.

Đáp án B

Ví dụ 2. Tính tổng tất cả các số nguyên dương n thỏa mãn A_n² - 3C_n² = 15 - 5n.

A. 13

B. 10

C. 12

D. 11

Hướng dẫn

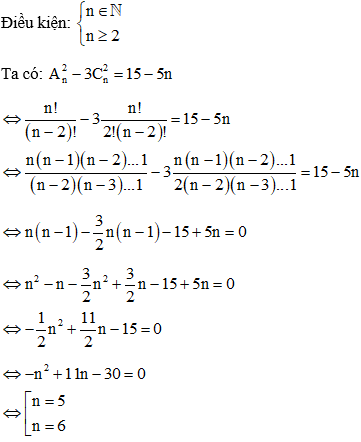
Đối chiếu điều kiện vậy n = 5 và n = 6.

Vậy tổng số nguyên dương n thỏa mãn yêu cầu là 5 + 6 = 11.

Đáp án D.

Ví dụ 3. Giải phương trình A_x³ + C_x^{x - 2} = 14x

A. Một số khác

B. x = 6

C. x = 5

D. x = 4

Hướng dẫn

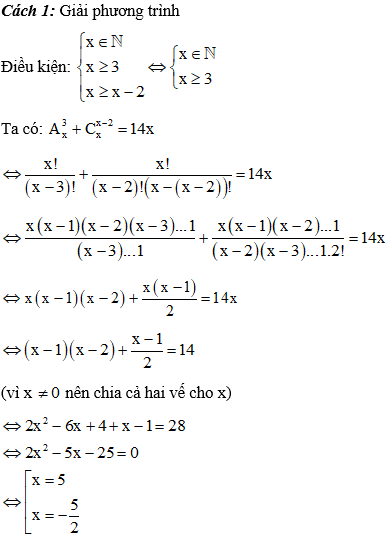
Kết hợp điều kiện vậy x = 5.

Cách 2: Thử các kết quả ở phần đáp án vào phương trình đã cho, thấy x = 5 thỏa mãn. (Cách này chỉ áp dụng cho trường hợp làm bài trắc nghiệm và có đáp án thỏa mãn)

Đáp án C

Ví dụ 4. Cho các số tự nhiên m, n thỏa mãn đồng thời các điều kiện C_m² = 153 và C_mⁿ = C_m^{n + 2}. Khi đó m + n bằng

A. 25

B. 24

C. 26

D. 23

Hướng dẫn

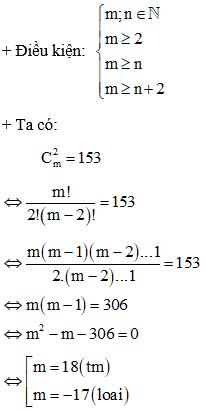
+ Theo tính chất C_n^k = C_n^{n - k}, vậy từ C_mⁿ = C_m^{n + 2}, suy ra n + 2 = m – n

⇔ 2n + 2 = m ⇔ 2n + 2 = 18 ⇔ n = 8(tm)

Vậy m + n = 18 + 8 = 26.

Đáp án C