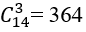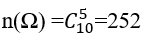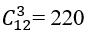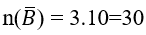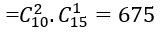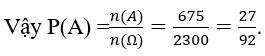Trắc nghiệm tính xác suất theo định nghĩa cổ điển - Toán lớp 11

---

Trắc nghiệm tính xác suất theo định nghĩa cổ điển

Với Trắc nghiệm tính xác suất theo định nghĩa cổ điển Toán lớp 11 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính xác suất theo định nghĩa từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

Bài 1: Một cái túi chứa 3 viên bi đỏ và 5 bi xanh, 6 viên bi vàng. Chọn ngẫu nhiên 3 viên bi. Xác suất để 3 viên bi có cả ba màu đỏ, xanh, vàng là:

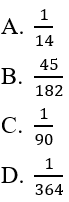
Lời giải:

Đáp án: B

Số các kết quả có thể xảy ra là

Gọi A là biến cố:" 3 bi xảy ra có cả 3 màu đỏ, xanh, vàng" thì

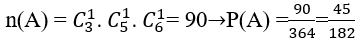
Bài 2: Gieo 3 con súc sắc cân đối, đồng chất và quan sát số chấm xuất hiện. Khi đó Xác suất để tổng số chấm xuất hiện trên mặt ba con súc sắc bằng 12 là:

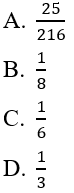
Lời giải:

Đáp án: A

Số khả năng xuất hiện S mỗi con xúc sắc là 6. Vì vậy số kết quả có thể xảy ra trên mặt xuất hiện của ba con xúc sắc là 6*6*6= 216

Gọi B là biến cố: " Tổng số chấm xuất hiện trên bề mặt con xúc sắc bằng 12"

Nhận thấy

12=4+4+4=5+4+3=5+5+2=6+4+2=6+5+1

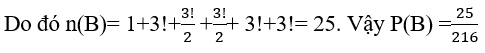
Bài 3: Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm. Tính xác suất để trong 5 sản phẩm được chọn đó không có phế phẩm nào:

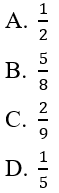
Lời giải:

Đáp án: C

Số khả năng chọn 5 sản phẩm trong 10 sản phẩm là

Gọi A là biến cố:" trong 5 sản phẩm được chọn không có phế phẩm nào"

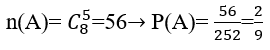
Bài 4: Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm. Tính xác suất để trong 5 sản phẩm được chọn co ít nhất 1 phế phẩm

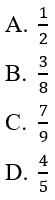
Lời giải:

Đáp án: D

Gọi B là biến cố:" trong 5 sản phẩm được chọn có ít nhất 1 phế phẩm" thì

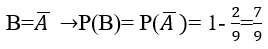
Bài 5: Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm. Tính xác suất để trong 5 sản phẩm được chọn có đúng 1 phế phẩm

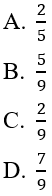
Lời giải:

Đáp án: B

Gọi C là biến cố:" trong 5 sản phẩm được chọn có đúng một phế phẩm"

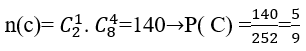
Bài 6: Trong một buổi liên hoan có 6 cặp nam nữ, trong đó có 3 cặp là vợ chồng. Chọn ngẫu nhiên 3 người trong số đó tham gia trò chơi. Tính xác suất để trong 3 người được chọn có đúng 1 người là nam

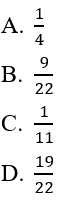
Lời giải:

Đáp án: B

Số khả năng chọn ngẫu nhiên 3 người từ 6*2= 12 người là

a. Gọi A là biến cố:" trong 3 người được chọn có đúng 1 nam"

Bài 7: Trong một bài thi trắc nghiệm khách quan có 20 câu, mỗi câu có 4 phương án trả lời trong đó chỉ có 1 phương án đúng. Một học sinh không học bài nên làm bài bài bằng cách chọn ngẫu nhiên mỗi câu một phương án. Tính xác suất để học sinh đó trả lời đúng 10 câu?

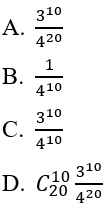
Lời giải:

Đáp án: D

Gọi Ai là biến cố:" học sinh chọn đúng ở câu i" i= 1,2,..,20

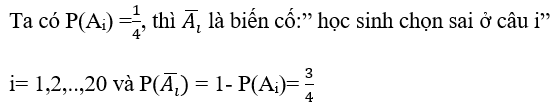
Gọi X là biến cố:" Học sinh trả lời đúng 10 câu trong 20 câu"

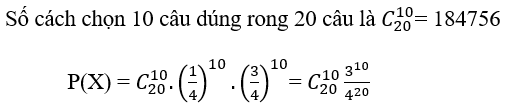
Bài 8: Có hai hộp bút chì. Hộp 1 có 3 bút đỏ và 4 bút xanh. Hộp II có 8 bút đỏ và 4 bút xanh. Chọn ngẫu nhiên từ mỗi hộp ra 1 bút. Tính xác suất để có 1 bút đỏ và 1 bút xanh.

Lời giải:

Đáp án: C

Gọi A là biến cố:" chọn bút đỏ ở hộ thứ i" i=1,2

B là biến cố:" chọn bút xanh ở hộp thứ i " i= 1,2

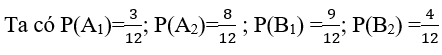
Gọi X là biến cố: " chọn được 1 bút đỏ và 1 bút xanh" thì X= A₁B₂ ∪ A₂ B₁

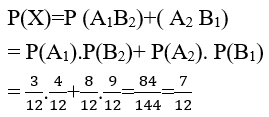
Bài 9: Một chiếc máy có ba động cơ I,II,III hoạt động độc lập với nhau. Xác xuất để động cơ I,II,III chạy tốt tương ứng là 0,7;0,8;0,9. Xác suất để cả 3 động cơ chạy tốt là:

Lời giải:

Đáp án: D

Gọi A_i là biến cố:" động cơ i chạy tốt" i=1,2,3

P(A₁)= 0,7 ; P(A₂).= 0,8 ; P(A₃)=0,9 và A₁, A₂, A₃ độc lập với nhau

A₁, A₂, A₃ là biến cố:" cả 3 biến cố đều chạy tốt "

P(A₁. A₂. A₃)= P(A₁). P(A₂). P(A₃)= 0,504

Bài 10: Một bộ bài tú lơ khơ gồm 53 con, lấy ngẫu nhiên lần lượt có hoàn lại từng con cho đến khi lần đầu tiên lấy được con át thì dừng. Tính xác suất sao cho quá trình dừng lại ở ngay lần thứ nhất:

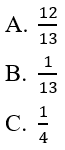
Lời giải:

Đáp án: B

Kí hiệu A_k: " lần thứ k lấy được con át" k ≥ 1 thì P(A₁)=4/52=1/13

Ta tính P(A₁)= 1/13

Bài 11: Trong một buổi liên hoan có 6 cặp nam nữ, trong đó có 3 cặp là vợ chồng. Chọn ngẫu nhiên 3 người trong số đó tham gia trò chơi. Tính xác suất để trong 3 người dược chọn không có cặp vợ chồng nào

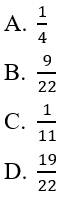
Lời giải:

Đáp án: D

Gọi B là biến cố :" trong 3 người được chọn không có cặp vợ chồng nào"

thì 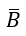là biến cố :" có đúng một cặp vợ chồng trong ba người được chọn"

Ta có

(vì có 3 cách chọn cặp vợ chồng, và 10 cách chọn người thứ 3 trong số 10 người còn lại) nên

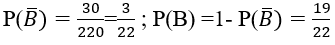
Bài 12: Hai xạ thủ cùng bắn mỗi nhười một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 1/2 và 1/3. Tính xác suất của biến cố X:"cả hai xạ thủ đều bắn trúng bia"

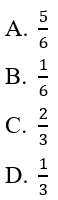
Lời giải:

Đáp án: B

.Gọi A là biến cố "Xạ thủ thứ i bắn trúng bia" i = 1,2.

Khi đó, P(A₁) =1/2; P(A₂) = 1/3; A₁ và A₂ độc lập với nhau

X =A₁ ∩ A₂ nên P(X) = P(A₁ ∩ A₂) = P(A₁.A₂) = P(A₁).P(A₂) = 1/6

Chọn đáp án là B

Bài 13: Lớp 11B có 25 đoàn viên trong đó có 10 nam và 15 nữ. Cho ngẫu nhiên 3 đoàn viên trong lớp để tham dự hội trại ngày 26 tháng 3. Tính xác suất để 3 đoàn viên được chọn có 2 nam và 1 nữ.

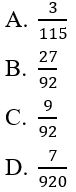
Lời giải:

Đáp án: D

Gọi A là biến cố:"3 đoàn viên được chọn có 2 nam và 1 nữ" thì số phần tử của tập A là

Bài 14: Một lớp học có 40 học sinh trong đó coa 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh. Xác suất của biến cố A:"học sinh được chọn giỏi Toán" là:

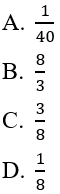
Lời giải:

Đáp án: C

Ta có n(Ω) = 40

Rõ ràng n(A) = 15 nên P(A) = 15/40 = 3/8

Chọn đáp án là C

Bài 15: Lấy ngẫu nhiên 1 thẻ từ 1 hộp 30 thẻ được đánh số từ 1 đến 30. Tính xác suất để thẻ được lấy ghi số 6

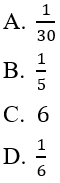
Lời giải:

Đáp án:

không gian mẫu Ω={1,2,..30}. kí hiệu A là biến cố " thẻ lấy ra ghi số 6", B là biến cố "thẻ lấy ra ghi số chia hết cho 5"

A={6}, n(A) =1,n(Ω) = 30

⇒ P(A) =1/30

Chọn đáp án A