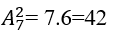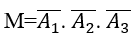Trắc nghiệm xác định phép thử, không gian mẫu và biến cố - Toán lớp 11
Trắc nghiệm xác định phép thử, không gian mẫu và biến cố
Với Trắc nghiệm xác định phép thử, không gian mẫu và biến cố Toán lớp 11 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập xác định phép thử, không gian mẫu và biến cố từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

Bài 1: Gieo hai đồng tiền một lần. Kí hiệu S,N để chỉ đông tiền lật sấp, lật ngửa.
Mô tả không gian mẫu
A. Ω ={SN,NS}
B. Ω ={NN,SS}
C. Ω ={S,N}
D. Ω ={SN,NS,SS,NN}
Lời giải:
Đáp án: D
Ω ={SN,NS,SS,NN}
Bài 2: Gieo hai đồng tiền một lần. Kí hiệu S,N để chỉ đông tiền lật sấp, lật ngửa.
Xác định biến cố M: "hai đông tiền xuất hiện hai mặt không giống nhau"
A. M={NN,SS}
B. M={NS,SN}
C. M={NS,NN}
D. M={SS,SN}
Lời giải:
Đáp án: B
M={NS,SN}
Bài 3: Một hộp có hai bi trắng được đánh số từ 1 đến 2, 3 viên bi xanh được đánh số từ 3 đến 5 và 2 viên bi đỏ được đánh số từ 6 đến 7. Lấy ngẫu nhiên hai viên bi:
Mô tả không gian mẫu
A. Ω ={(m,n)|1 ≤ m ≤ 7,1 ≤ n ≤ 7}
B. Ω ={(m,n)|1 ≤ m ≤ 7,1 ≤ n ≤ 7,m ≠ n}
C. Ω ={(m,n)|1 ≤ m ≤ 5,6 ≤ n ≤ 7}
D. Ω ={(m,n)|1 ≤ m ≤ 3,4 ≤ n ≤ 7}
Lời giải:
Đáp án: B
Mỗi viên bi đánh một số, nên 2 viên bi lấy ra mang số khác nhau. Vậy
Ω ={(m,n)|1 ≤ n ≤ 7 và m ≠ n}
Bài 4: Một hộp có hai bi trắng được đánh số từ 1 đến 2, 3 viên bi xanh được đánh số từ 3 đến 5 và 2 viên bi đỏ được đánh số từ 6 đến 7. Lấy ngẫu nhiên hai viên bi:
Số phần tử của không gian mẫu là:
A. 49
B. 42
C. 10
D. 12
Lời giải:
Đáp án: B
Mỗi phần tử của không gian mẫu là một chỉnh hợp chập 2 của 7 vì vậy số phần tử của không gian mẫu là
Bài 5: Một hộp có hai bi trắng được đánh số từ 1 đến 2, 3 viên bi xanh được đánh số từ 3 đến 5 và 2 viên bi đỏ được đánh số từ 6 đến 7. Lấy ngẫu nhiên hai viên bi:
Phát biểu biến cố M={(1,2),(3,4),(3,5),(4,5),(6,7)} dưới dạng mệnh đề
A. Hai bi lấy ra cùng màu trắng
B. Hai bi lấy ra cùng màu xanh
C. Hiệu hai số của hai bi không lớn hơn hai
D. Hai bi lấy ra cùng màu
Lời giải:
Đáp án: D
Có hai bi trắng được đánh số từ 1 đến 2, 3 viên bi xanh được đánh số từ 3 đến 5 và 2 viên bi đỏ được đánh số từ 6 đến 7 nên ta chọn D

Bài 6: Từ các chữ số 1,2,3,4 nhười ta lập các số tự nhiên có 3 chữ số khác nhau. Tính số phần tử không gian mẫu
A. 16 B. 24 C. 6 D. 4
Lời giải:
Đáp án: B
Ta lập được 4!=24 số
Bài 7: Từ các chữ số 1,2,3,4 nhười ta lập các số tự nhiên có 3 chữ số khác nhau.
Phát biểu biến cố A={123,234,124,134} dưới dạng mệnh đề
A. Số tự nhiên có ba chữ số được thành lập từ các chữ số 1,2,3,4
B. Số tự nhiên có ba chữ số được thành lập có chữ số đứng sau lớn hơn chữ số đứng trước
C. Số tự nhiên có ba chữ số được thành lập chia hết cho 2 hoặc 3
D. Số tự nhiên có ba chữ số được thành lập có chữ số tận cùng là 3 hoặc 4
Lời giải:
Đáp án: B
Ta thấy các chữ số hàng chục lớn hơn hàng đơn vị, hàng trăm lớn hơn hàng chục chọn B
Bài 8: Có hai hộp thẻ. Hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 5, hộp thứ hai chứa các thẻ được đánh số từ 6 đến 9. Lấy ngẫu nhiên ở mỗi hợp 1 thẻ
Hãy mô tả không gian mẫu, kí hiệu "ab" thể hiện hộp thứ nhất lấy thể đánh số a, hộp thứ hai lấy thẻ đánh số b.
A. Ω ={16,27,38,49,56}
B. Ω ={19,28,37,46,57}
C. Ω ={16,17,18,19,26,27,28,29,36,37,38,39,46,47,48,49,56,57,58,59}
D. Ω ={61,62,63,64,65,71,72,73,74,75,81,82,83,84,85,91,92,92,94,95}
Lời giải:
Đáp án: C
Ω ={16,17,18,19,26,27,28,29,36,37,38,39,46,47,48,49,56,57,58,59}
Vì hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 5, hộp thứ hai chứa các thẻ được đánh số từ 6 đến 9 chọn C
Bài 9: Có hai hộp thẻ. Hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 5, hộp thứ hai chứa các thẻ được đánh số từ 6 đến 9. Lấy ngẫu nhiên ở mỗi hợp 1 thẻ
Xác định biến cố M:"tổng các số ở hai thẻ lấy ra là số nguyên tố"
A. M={16,38,49,56}
B. M={16,29,38,47,49,56,58}
C. M={61,74,92,94,65}
D. M={16,38,56}
Lời giải:
Đáp án: B
M={16,29,38,47,49,56,58} tổng 2 chữ số là số nguyên tố
Bài 10: Có ba xạ thủ đi săn đêm. Gọi Ak là biến cố:"xạ thủ thứ k bắn trúng đích" với k = 1,2,3.
Hãy dùng các phép toán nêu các biến cố biểu thị qua A1, A2, A3.
Biến cố M: "không có xạ thủ nào bắn trúng đích"
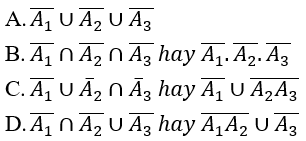
Lời giải:
Đáp án: B
: Theo bài ra biến cố Ak: " xạ thủ thứ k bắn trúng đích ", với k=1,2,3 thì biến cố đối 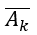
Biến cố M " không có xạ thủ nào bắn trúng đích" , tức là cả ba xạ thủ đều bắn trượt nên

Bài 11: Có ba xạ thủ đi săn đêm. Gọi Ak là biến cố:"xạ thủ thứ k bắn trúng đích" với k = 1,2,3.
Hãy dùng các phép toán nêu các biến cố biểu thị qua 1, A2, A3.
Biến cố N:"có đúng hai xạ thủ trúng đích"
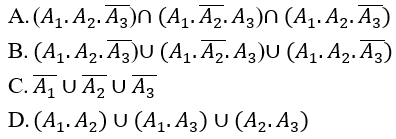
Lời giải:
Đáp án: B
Biến cố N: " có đúng hai xạ thủ bắn trúng đích" tức là trong ba xạ thủ có hai người bắn trúng và một người bắn trượt
Bài 12: Một nhóm bạn có 4 bạn gồm 2 bạn Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan
Tính số phần tử của không gian mẫu
A. 6 B. 24 C. 1 D. 4
Lời giải:
Đáp án: B
Mỗi cách xắp sêp 4 bạn vào 4 chỗ ngồi là một hoán vị của 4 phần tử. Vì vậy số phần tử của không gian mẫu là 4! =24
Bài 13: Một nhóm bạn có 4 bạn gồm 2 bạn Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan
Xác định biến cố M:"xếp hai nam ngồi cạnh nhau"
A. M={(MDHL),(HMDL),(HLMD)}
B. M={(MDHL),(LMDH),(LHMD)}
C. M={(MDHL),(MDLH),(HMDL),(LMDH),(HLMD),(LHMD)}
D. M={(MDHL),(DMHL),(MDLH),(DMLH),(HMDL),(HDML),(LMDH),(LDMH),(HLMD),(HLDM),(LHMD),(LHDM)}
Lời giải:
Đáp án: D
Đánh số ghế theo thứ tự 1,2,3,4. Hai bạn nam ngồi cạnh nhau ở vị trí ( 1 và 2) hoặc (2 và 3) hoặc (3 và 4). Nếu hai bạn nam đổi chỗ cho nhau( giữ nguyên chỗ hai bạn nữ) thì ta có một cách xếp mới . Vì vậy cần chọn phương án D
Bài 14: Một nhóm bạn có 4 bạn gồm 2 bạn Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan
Tìm số phần tử của biến cố N:"xếp nam và nữ ngồi xen kẽ nhau"
A. 24 B. 4 C. 8 D. 6
Lời giải:
Đáp án: C
Trường hợp 1: bạn nam ngồi đầu. khi dó 2 bạn nam xếp vào 2 chỗ ( số ghế 1 và 3), nữ xếp nốt vào hai chỗ còn lại ( ghế số 2 và 4), số cách xếp là 2!.2!=4
Trường hợp 2: bạn nữ ngồi đầu. Tương tự có 4 cách xếp . Vậy theo quy tắc cộng số phần tử của biến cố N là 4+4=8
Bài 15: Gieo ngẫu nhiên ba đồng xu phân biệt một lần. Kí hiệu S, N lần lượt chỉ đồng xu lật sấp, lật ngửa
Hãy mô tả không gian mẫu
A. Ω ={S,N,S}
B. Ω ={SSS,SSN,SNS,NSS}
C. Ω ={SSS,SSN,SNS,NSS,NNS,NSN,SNN,NNN}
D. Ω ={NNN,NSN,SNS}
Lời giải:
Đáp án: C
Mỗi phần tử của không gian mẫu chỉ rõ ba đồng tiền xuất hiện ngẫu nhiên mặt sấp hay mặt ngửa. Vì vậy cần chọn phương án C