Xác định giao điểm của đường thẳng và mặt phẳng lớp 11 (bài tập + lời giải)
Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Xác định giao điểm của đường thẳng và mặt phẳng lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Xác định giao điểm của đường thẳng và mặt phẳng.
Xác định giao điểm của đường thẳng và mặt phẳng lớp 11 (bài tập + lời giải)
1. Phương pháp giải
- Với bài toán tìm giao điểm của một đường thẳng d và mặt phẳng (P) cho trước:
+ Chọn một mặt phẳng phụ (M) chứa đường thẳng d.
+ Tìm giao tuyến của (P) và (M). Gọi .
+ Tìm giao điểm của a và d. Gọi .
+ A chính là giao điểm của d và (P).
2. Ví dụ minh họa
Ví dụ 1.
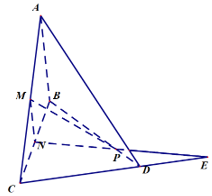
Cho 4 điểm A, B, C, D không đồng phẳng và không có 3 điểm nào thẳng hàng. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD. Xác định giao điểm của đường thẳng CD và mặt phẳng (MNP)?
Hướng dẫn giải:
Gọi giao điểm của NP và CD là E.
CD thuộc mặt phẳng (BCD).
Do nên .
N nằm trên BP, P nằm trên BD nên NP nằm trên mặt phẳng (BCP).
Do đó NP là giao tuyến của (MNP) và (BCD).
Mà nên E là giao điểm của CD và (MNP).
3. Bài tập tự luyện
Bài 1. Với một đường thẳng d bất kỳ và một mặt phẳng (P), trường hợp mối quan hệ có thể xảy ra là
A. d nằm trên (P);
B. d song song với (P);
C. d cắt (P);
D. Cả ba phương án trên.
Bài 2. Với đường thẳng d nằm trên mặt phẳng (P) thì d và (P) có
A. Không điểm chung;
B. Một điểm chung duy nhất;
C. Vô số điểm chung;
D. Cả ba phương án trên.
Bài 3. Với đường thẳng d song song với mặt phẳng (P) thì d và (P) có
A. Không điểm chung;
B. Một điểm chung duy nhất;
C. Vô số điểm chung;
D. Cả ba phương án trên.
Bài 4. Với đường thẳng d đi qua mặt phẳng (P) thì d và (P) có
A. Không điểm chung;
B. Một điểm chung duy nhất;
C. Vô số điểm chung;
D. Cả ba phương án trên.
Bài 5. Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng (ACD) là:
A. Điểm F;
B. Giao điểm của EG và AC;
C. Giao điểm của EG và CD;
D. Giao điểm của EG và AF.
Bài 6. Có 4 điểm A, B, C, D không đồng phẳng. Lấy hai điểm E và F trên AD và AB sao cho EF không song song với BD. Giao điểm của đường thẳng EF với (BCD) là
A. Giao điểm của EF và BD;
B. Giao điểm của EF và BC;
C. Giao điểm của EF và BA;
D. Giao điểm của EF và AD.
Bài 7. Cho hai mặt phẳng (M) và (P). Gọi a là giao tuyến của hai mặt phẳng này. Với một đường thẳng d bất kỳ thuộc mặt phẳng (M), giao điểm của d với (P) là
A. Một điểm nằm trên (M) và không nằm trên (P);
B. Một điểm nằm trên (P) và không nằm trên (M);
C. Một điểm không nằm trên cả (M) và (P);
D. Một điểm nằm trên cả (M) và (P).
Bài 8. Giao điểm của MN và (ABC) là
A. Điểm M;
B. Điểm N;
C. Điểm O;
D. Điểm B.
Bài 9. Giao điểm của BD và (SAC) là
A. Điểm M;
B. Điểm N;
C. Điểm O;
D. Điểm B.
Bài 10. Giao điểm của AM và (SBD) là
A. Giao điểm của AM và SO;
B. Giao điểm của AM và BD;
C. Giao điểm của AM và BC;
D. Giao điểm của AM và SC.