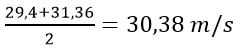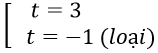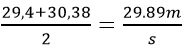Dạng bài tập Ý nghĩa của đạo hàm (Vật Lí, Cơ học, Hình học) hay, chi tiết - Toán lớp 11
Dạng bài tập Ý nghĩa của đạo hàm (Vật Lí, Cơ học, Hình học) hay, chi tiết
Với Dạng bài tập Ý nghĩa của đạo hàm (Vật Lí, Cơ học, Hình học) hay, chi tiết Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Ý nghĩa của đạo hàm (Vật Lí, Cơ học, Hình học) từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải & Ví dụ
Ví dụ minh họa
Ý nghĩa vật lí :
Vận tốc tức thời của chuyển động thẳng xác định bởi phương trình : s = s(t) tại thời điểm to là v(to) = s’(to)
Cường độ tức thời của điện lượng Q = Q(t) tại thời điểm to là : I(to) = Q’(to).
Ý nghĩa cơ học của đạo hàm cấp hai
Đạo hàm cấp hai f ''(x) là gia tốc tức thời cảu chuyển động s = f(t) tại thời điểm t
Ý nghĩa hình học của đạo hàm:
Nếu tồn tại, f '(xo ) là hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại Mo(xo; f(xo)). Khi đó phương trình tiếp tuyến của đồ thị hàm số tại là Mo
y - yo = f '(xo)(x - xo)
Bài 1: Một vật rơi tự do theo phương trình s = (1/2)gt2, trong đó g ≈ 9,8 m/s2 là gia tốc trọng trường. Tính vận tốc tức thời của chuyển động tại thời điểm t = 5s
Hướng dẫn:
Ta có vận tốc của chuyển động: v = (s)’ = gt
Khi đó vận tốc tức thời của chuyển động tại thời điểm t = 5s là: 9,8.5 = 49 m/s
Bài 2: Xét chuyển động có phương trình
s(t) = Asin(ωt + φ) (A, ω, φ là những hằng số).
Tìm gia tốc tức thời tại thời điểm t của chuyển động
Hướng dẫn:
Ta có gia tốc tức thời tại thời điểm t của chuyển động là:
a(t) = s '' (t) = (Aω cos(ωt + φ) )' = -Aω2 sin(ωt + φ)
Bài 3: Một chuyển động thẳng xác định bởi ph¬ương trình s = (1/3)t3 - t2 + 5t, trong đó t tính bằng giây và s tính bằng mét. Gia tốc của chuyển động khi t = 4 là bao nhiêu?
Hướng dẫn:
Gia tốc của chuyển động khi t là :
a(t) = (s(t)) '' = (t2-2t+5)' = 2t-2
Gia tốc của chuyển động khi t = 4 là : a(4) = 6 m/s2
Bài 4: Một vật rơi tự do theo phương trình s = (1/2)gt2, trong đó g ≈ 9,8 m/s2 là gia tốc trọng trường.Vận tốc trung bình của chuyển động trong khoảng thời gian t (t = 3s) đến t + Δt (Δt = 0,2s) là:
Hướng dẫn:
Vận tốc của chuyển động tại thời điểm t là:
v(t) = (s(t))' = gt
Tại t = 3: v = 29,4 m/s
Tại t + Δt = 3,2s: v = 31,36 m/s
Khi đó vận tốc trung bình là:
Bài 5: Một chuyển động thẳng xác định bởi ph¬ương trình s = 2t3+5t+2, trong đó t tính bằng giây và s tính bằng mét. Vận tốc của chuyển động khi t = 3 là
Hướng dẫn:
Vận tốc của chuyển động tại thời điểm t là:
v(t) = (s(t))' = 6t2 + 5
v(3) = 59 m/s
Bài 6: Một chuyển động thẳng xác định bởi ph¬ương trình s = t3-3t2-9t+2, trong đó t tính bằng giây và s tính bằng mét. Tính gia tốc tại thời điểm vận tốc triệt tiêu.
Hướng dẫn:
Vận tốc của chuyển động tại thời điểm t là:
v(t) = (s(t))' = 3t2 - 6t - 9
v(t) = 0 ⇔
Gia tốc của chuyển động khi t là :
a(t) = (v(t))' = 6t - 6
Ta có gia tốc tại thời điểm vận tốc triệt tiêu là: a(3) = 12 m/s2
Bài 7: Một chuyển động thẳng xác định bởi phương trình s = t3 - 3t2 + 9t, trong đó t tính bằng giây và s tính bằng mét. Tính vận tốc tại thời điểm gia tốc triệt tiêu.
Hướng dẫn:
Vận tốc của chuyển động tại thời điểm t là:
v(t) = (s(t))' = 3t2 - 6t + 9
Gia tốc của chuyển động khi t là :
a(t) = (v(t))' = 6t - 6
a(t) = 0 ⇔ t = 1
Ta có vận tốc tại thời điểm gia tốc triệt tiêu là v(1) = 6 m/s

B. Bài tập vận dụng
Bài 1: Một chuyển động thẳng xác định bởi phương trình s = t3-3t2+5t+2, trong đó t tính bằng giây và s tính bằng mét. Gia tốc của chuyển động khi t = 3 là:
A. 24 m/s2 B. 17 m/s2 C. 14 m/s2 D. 12 m/s2
Lời giải:
Đáp án: D
Đáp án D
Ta có gia tốc tức thời của chuyển động tại thời điểm t bằng đạo hàm cấp hai của phương trình chuyển động tại thời điểm t.
s ' = (t3-3t2+5t+2)' = 3t2-6t+5
s ' = 6t - 6 ⇒ s ''(3) = 12
Bài 2: Cho chuyển động thẳng xác định bởi phương trình s = t3-3t2-9t+2 (t tính bằng giây; s tính bằng mét). Khẳng định nào sau đây đúng ?
A. Vận tốc của chuyển động bằng 0 khi t = 0 hoặc t = 2
B. Vận tốc của chuyển động tại thời điểm t = 2 là v = 18 m/s
C. Gia tốc của chuyển động tại thời điểm t = 4 là a = 12 m/s2
D. Gia tốc của chuyển động bằng 0 khi t = 0
Lời giải:
Đáp án: C
Đáp án C
Ta có gia tốc tức thời của chuyển động tại thời điểm t bằng đạo hàm cấp hai của phương trình chuyển động tại thời điểm t.
s' =(t3-3t2+5t+2)' = 3t2-6t+5
s' = 6t-6 ⇒ s ''(3) = 12
Bài 3: Cho chuyển động thẳng xác định bởi phương trình s = t3-3t2 (t tính bằng giây; stính bằng mét). Khẳng định nào sau đây đúng?
A. Gia tốc của chuyển động khi t = 4s là a = 18 m/s2
B. Gia tốc của chuyển động khi t = 4s là a = 9 m/s2
C. Vận tốc của chuyển động khi t = 3s là v = 12 m/s
D. Vận tốc của chuyển động khi t = 3s là v = 24 m/s
Lời giải:
Đáp án: A
Đáp án A
s' = 3t2-6t ⇒ s '' = 6t - 6
s ''(4) = 18 m/s2
Bài 4: Một chất điểm chuyển động thẳng có phương trình S = (1/2)t2 (t là thời gian tính bằng giây (s), S là đường đi tính bằng mét). Tính vận tốc (m/s) của chất điểm tại thời điểm t0 = 5(s)
A. 5/2 B. 5 C. 25 D. 12,5
Lời giải:
Đáp án: B
s' = v(t) = t ⇒ v(5) = 5 m/s. Đáp án B
Bài 5: Cho biết điện lượng truyền trong dây dẫn theo thời gian biểu thị bởi hàm số Q(t) = 2t2 + t, trong đó t được tính bằng giây (s) và Q được tính theo Culong (C). Tính cường độ dòng điện tại thời điểm t = 4s.
A. 13
B. 16
C. 36
D. 17
Lời giải:
Đáp án: D
Q'(t) = I(t) = 4t + 1 ⇒ t(4) = 17. Đáp án D
Bài 6: Một chất điểm chuyển động thẳng, quãng đường đi được xác định bởi phương trình (t) = t3 - 4t2 - 2t + 1 , t tính bằng giây (s), S tính bằng mét. Gia tốc (m/s2) chuyển động của chất điểm khi t = 3s là:
A. 10
B. 8
C. 18
D. 1
Lời giải:
Đáp án: A
s' = v(t) = 3t2-8t-2, s'' = a(t) = 6t - 8 ⇒ a(3) = 10 m/s2. Đáp án A
Bài 7: Một chất điểm chuyển động thẳng, quãng đường đi được xác định bởi phương trình S = t3-5t2-9t+3, t tính bằng giây (s), S tính bằng mét. Gia tốc (m/s2) chuyển động của chất điểm khi t = 2s là:
A. 2
B. -5
C. -27
D. 22
Lời giải:
Đáp án: A
s' = v(t) = 3t2-10t-9, s'' = a(t) = 6t - 10 ⇒ a(2) = 2 m/s2. Đáp án A

Bài 8: Tính giá trị gần đúng (chính xác đến 3 chữ số thập phân, với π ≈ 3,141) của diện tích hình tròn có bán kính bằng 4,05 m.
A. 50,570 m2
B. 50,884 m2
C. 51,52 m2
D. 52 m2
Lời giải:
Đáp án: C
S = π.r2 = 3,141.4,052 = 51,52 m2. Đáp án C
Bài 9: Cho đường cong có phương trình y = x2 - 2x + 1. Hệ số góc của tiếp tuyến đường cong đó tại điểm có hoành độ bằng 1 là:
A. 1
B. -1
C. 0
D. 2
Lời giải:
Đáp án: C
y’ = 2x – 2. y’(1) = 0. Đáp án C
Bài 10: Cho đường cong có phương trình y = x4-x2+1. Tiếp tuyến của đường cong đó tại điểm có hoành độ bằng -1 đi qua điểm:
A. M(0, 4)
B. M(1, -3)
C. M(-2, -1)
D. N(2, -3)
Lời giải:
Đáp án: B
y' = 4x3-2x, y'(-1) = -2. Phương trình tiếp tuyến tại điểm có hoành độ -1 là:
y = -2(x + 1) + 1 = -2x – 1
Vậy tiếp tuyến qua điểm M(1; -3). Đáp án B
Bài 11: Cho biết điện lượng truyền trong dây dẫn theo thời gian biểu thị bởi hàm số Q(t)= 2t2 + t, trong đó t được tính bừng giây (s) và Q được tính theo culong (C). Tính cường độ dòng điện tại thời điểm t = 2s.
A. 9
B. 10
C. 9
D. 6
Cho bài toán sau:
Một chất điểm chuyển động thẳng có phương trình S = t3-3t2+5t+3 (t là thời gian tính bằng giây (s), S là đường tính bằng mét).
Lời giải:
Đáp án: A
Q'(t) = I(t) = 4t + 1 ⇒ t(2) = 9. Đáp án A
Bài 12: Tính vận tốc (m/s) của chất điểm tại thời điểm t0 = 2s
A. 9
B. 5
C. 9
D. 8
Lời giải:
Đáp án: B
s' = v(t) = 3t2-6t+5 ⇒ v(2) = 5 m/s. Đáp án B
Bài 13: Tính gia tốc (m/s2) của chất điểm tại thời điểm t0 = 2s
A. 12
B. 5
C. 11
D. 6
Cho bài toán sau:
Một vật rơi tự do theo phương trình s = (1/2)gt2, trong đó g ≈ 9,8 m/s2 là gia tốc trọng trường
Lời giải:
Đáp án: D
s'' = a(t) = 6t - 6 ⇒ a(2) = 6 m/s2. Đáp án D
Bài 14: Vận tốc trung bình của chuyển động trong khoảng thời gian t (t = 3s) đến t + Δt (Δt = 0,1s) là:
A. 30 m/s B. 29.89 m/s C. 30,56 m/s D. 30,51 m/s
Lời giải:
Đáp án: B
Vận tốc của chuyển động tại thời điểm t là:
v(t) = (s(t))' = gt
Tại t = 3: v = 29,4 m/s
Tại t + Δt = 3,1s : v = 30,38 m/s
Khi đó vận tốc trung bình là:
Đáp án B
Bài 15: Vận tốc tức thời của chuyển động tại thời điểm t = 2s là:
A. 19,05 m/s B. 19 m/s C. 19,6 m/s D. 10 m/s
Lời giải:
Đáp án: C
v(2) = 19,6 m/s. Đáp án C