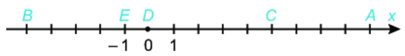Xác định phần dấu và phần số tự nhiên của một số nguyên. Tìm số đối của số nguyên lớp 6 (bài tập + lời giải)

---

Haylamdo biên soạn và sưu tầm chuyên đề phương pháp giải bài tập Xác định phần dấu và phần số tự nhiên của một số nguyên. Tìm số đối của số nguyên lớp 6 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Xác định phần dấu và phần số tự nhiên của một số nguyên. Tìm số đối của số nguyên.

Xác định phần dấu và phần số tự nhiên của một số nguyên. Tìm số đối của số nguyên lớp 6 (bài tập + lời giải)

1. Phương pháp giải

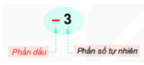
* Mỗi số nguyên (dương hoặc âm) có hai phần: phần dấu và phần số tự nhiên, phần dấu đúng trước phần số tự nhiên.

Ví dụ:

Cách xác định phần dấu và phần số tự nhiên của một số nguyên:

Bước 1: Xác định phần dấu. Phần dấu chính là phần đầu tiên của số, nếu trước số đó không có dấu gì thì chính là mang dấu +.

Bước 2: Phần đứng sau phần dấu chính là phần số tự nhiên. Lưu ý rằng phần số tự nhiên luôn là số nguyên lớn hơn hoặc bằng 0.

* Hai số đối nhau: Hai số đối nhau có tổng bằng 0.

Cho số nguyên a, số đối của số nguyên a là -a. Nghĩa là, muốn tìm số đối của một số, ta chỉ cần đổi dấu của nó. Đặc biệt, số đối của 0 chính là 0.

2. Ví dụ minh họa:

Ví dụ 1. Hãy xác định phần dấu và phần số tự nhiên của các số nguyên sau: -2; 7; -5; 4.

Hướng dẫn giải:

Số nguyên	Phần dấu	Phần số tự nhiên
-2	-	2
7	+	7
-5	-	5
4	+	4

Ví dụ 2. Tìm số đối của các số nguyên sau: 2; -4; 6; -7.

Hướng dẫn giải:

Theo nguyên tắc của tìm số đối của một đó là ta đổi dấu của số đó.

Vậy số đối của các số nguyên trên lần lượt là: -2; 4; -6; 7.

Ví dụ 3. Tìm số đối của 3 và -5, sau đó cho biết điểm biểu diễn hai số vừa tìm được trên hệ tọa độ cách nhau bao nhiêu đơn vị.

Hướng dẫn giải:

Số đối của 3 là -3, số đối của -5 là 5. Ta có hệ trục tọa độ biểu diễn:

Vậy điểm biểu diễn 2 số vừa tìm được cách nhau 8 đơn vị.

3. Bài tập tự luyện

Bài 1. Hãy xác định phần số tự nhiên của -4?

A. -4;

B. 4;

C. 2;

D. 1.

Bài 2. Hãy xác định phần dấu của -7?

A. +;                       

B. 7;

C. -;

D. -7.

Bài 3. Cho số nguyên sau: -10. Chọn phương án đúng?

A. Phần dấu của -10 là +;                       

B. Phần số tự nhiên của -10 là -10;

C. Phần số tự nhiên của -10 là 5;

D. Phần dấu của -10 là -.

Bài 4. Tìm số đối của số nguyên sau: -5.

A. 5;

B. 0;

C. 4;

D. -5.

Bài 5. Hãy xác định phần dấu và phần số tự nhiên của số đối của 15.

A. Số cần tìm có phần dấu là + và phần số tự nhiên là -15;

B. Số cần tìm có phần dấu là - và phần số tự nhiên là 15;

C. Số cần tìm có phần dấu là + và phần số tự nhiên là 15;

D. Số cần tìm có phần dấu là - và phần số tự nhiên là -15.

Bài 6. Cho hình vẽ sau. Hãy tìm số đối của số nguyên được biểu diễn bởi điểm E?

A. 1;

B. 0;

C. -4;

D. -1.

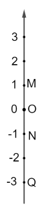
Bài 7. Số đối của các số nguyên được biểu diễn bới các điểm M, N và Q trong hình dưới đây lần lượt là?

A. -3, -1, 1;

B. -2, -1, 0;

C. -1, -1, -3;

D. -1, 1, 3.

Bài 8. Cho tập hợp E = {2; 4; -4; 5; 7; 0}. Hãy viết tập hợp D gồm các phần tử là số đối của các phần tử thuộc tập hợp E.

A. D = {2; -4; 4; -5; 7; 0};

B. D = {-2; -4; 4; -5; -7; 0};

C. D = {2; 4; -4; -5; 7; 0};

D. D = {2; -4; 4; 5; -7; 0}.

Bài 9. Cho tập hợp A = {-1; 2; -5; 3; -8}. Hãy viết tập hợp B gồm các phần tử là số đối của các phần tử thuộc tập hợp A.

A. B = {1; -2; 5; -3; 8};

B. B = {-1; -2; 5; -3; 8};

C. B = {1; -2; -5; -3; 8};

D. B = {1; -2; 5; -3; -8}.

Bài 10. Cho tập hợp I = {0; -3; 1; -5; 4; -6}. Tập hợp K gồm các phần tử là số đối của các phần tử thuộc tập hợp I. Khẳng định nào sau đây là đúng?

A. $-5\in K$ ;

B. $-4\notin K$;

C. $5\in K$;

D. $6\notin K$.