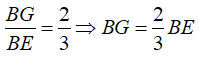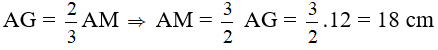Bài tập Tính chất ba đường trung tuyến của tam giác có lời giải - Toán lớp 7
Bài tập Tính chất ba đường trung tuyến của tam giác có lời giải
Với bộ Bài tập Tính chất ba đường trung tuyến của tam giác Toán lớp 7 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 7.

Bài 1: Chọn câu sai:
A. Trong một tam giác có ba đường trung tuyến
B. Các đường trung tuyến của tam giác cắt tại một điểm
C. Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó
D. Một tam giác có hai trọng tâm
Một tam giác chỉ có một trọng tâm nên D sai.
Chọn đáp án D.
Bài 2: Điền số thích hợp vào chỗ trống: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy”
A. 2/3 B. 3/2 C. 3 D. 2
Định lý: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy
Số cần điền là 2/3.
Chọn đáp án A.
Bài 3: Cho hình vẽ sau:
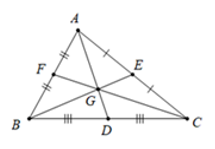
Điền số thích hợp vào chỗ chấm: BG = ....BE
A. 2 B. 3 C. 1/3 D. 2/3
Ta có AD, BE, CF là ba đường trung tuyến của tam giác ABC và chúng cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Theo tính chất ba đường trung tuyến của tam giác ta có:
Vậy số thích hợp điền vào chỗ chấm là: 2/3
Chọn đáp án D.
Bài 4: Cho hình vẽ sau:

Điền số thích hợp vào chỗ chấm: AG = ....GD
A. 2 B. 3 C. 1/3 D. 2/3
Ta có AD, BE, CF là ba đường trung tuyến của tam giác ABC và chúng cắt nhau tại G nên G là trọng tâm của tam giác ABC .
Theo tính chất ba đường trung tuyến của tam giác ta có:
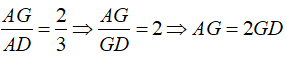
Vậy số thích hợp điền vào chỗ chấm là: 2
Chọn đáp án A.
Bài 5: Tam giác ABC có trung tuyến AM = 9cm và trọng tâm G. Độ dài đoạn AG là:
A. 4,5cm B. 3cm C. 6cm D. 4cm
Vì G là trọng tâm của tam giác ABC và AM là đường trung tuyến nên AG = (2/3)AM (tính chất ba đường trung tuyến của tam giác)
Do đó: AG = (2/3).9 = 6cm
Chọn đáp án C.
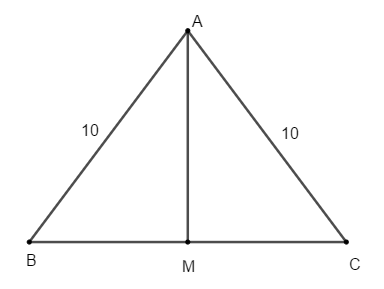
Bài 6: Cho ΔABC cân. Biết AB = AC = 10cm, BC = 12cm. M là trung điểm B
C. Độ dài trung tuyến AM là:
A. 22cm.
B. 4cm.
C. 8cm.
D. 6cm.
Chọn đáp án C
Bài 7: Cho ΔABC có M là trung điểm của BC. G là trọng tâm của tam giác và AG = 12cm. Độ dài đoạn thẳng AM =?
A. 18cm.
B. 16cm.
C. 14cm.
D. 13cm.
M là trung điểm của BC nên AM là đường trung tuyến kẻ từ A của tam giác ABC
Mà G là trọng tâm của tam giác ABC
Do đó:
Vậy AM = 18 cm.
Chọn đáp án A
Bài 8: Cho ΔABC vuông tại A. Nếu AM là đường trung tuyến thì:
A. AM ⊥ BC
B. AM = MC.
C. M trùng với đỉnh A.
D. M nằm ở trong ΔABC
+ Ta có AM là trung tuyến thì M là trung điểm cạnh BC, nên M ≠ A nên C sai.
+ Tương tự M nằm trên cạnh BC nên M không nằm trong tam giác ABC, nên D sai.
+ AM ⊥ BC khi tam giác ABC là tam giác cân (Theo chứng minh ở câu 6), nên A sai.
Vậy B là đáp án đúng.
Ta chứng minh B đúng như sau:
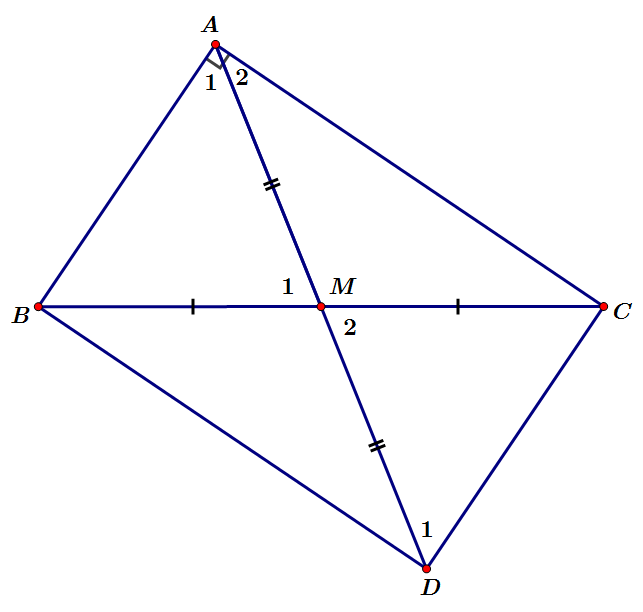
Trên tia đối của tia MA lấy điểm D sao cho MA = MD
Xét tam giác AMB và tam giác DMC, ta có:
MA = MD (ta dựng)
MB = MC (M là trung điểm BC)
Chọn đáp án B
Bài 9: Cho tam giác ABC. Trên đường trung tuyến AM của tam giác đó, lấy hai điểm D và E sao cho AD = DE = EM. Gọi O là trung điểm của đoạn thẳng DE. Khi đó trọng tâm của tam giác ABC là:
A. Điểm D
B. Điểm E
C. Điểm O
D. Cả A, B, C đều sai
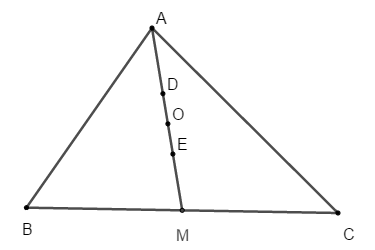
Ta có: D, E, O thuộc trung tuyến AM
Mà AD = DE = EM; O là trung điểm của DE
Nên AD = 1/3 AM; AE = 2/3 AM;
O là trung điểm của AM
Khi đó E là trọng tâm của tam giác ABC
(khoảng cách từ đỉnh tới trọng tâm của tam giác bằng 2/3 độ dài đường trung tuyến kẻ từ đỉnh đó).
Chọn đáp án B
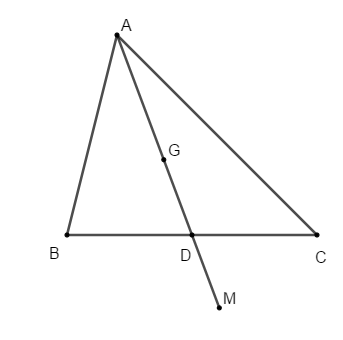
Bài 10: Cho tam giác ABC có G là trọng tâm, đường trung tuyến AD. Trên tia đối của tia DA lấy điểm M sao cho DM = 1/3 AD. Khẳng định nào là đúng trong số các khẳng định dưới đây?
A. D là trung điểm của GM.
B. G là trung điểm của AD.
C. AD = 3/4 GM.
D. AG = 3DM.
Chọn đáp án A