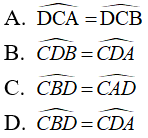Bài tập Tính chất đường trung trực của một đoạn thẳng có lời giải - Toán lớp 7
Bài tập Tính chất đường trung trực của một đoạn thẳng có lời giải
Với bộ Bài tập Tính chất đường trung trực của một đoạn thẳng Toán lớp 7 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 7.

Bài 1: Cho điểm C thuộc trung trực của đoạn thẳng AB. Biết CA = 10 cm. Độ dài đoạn thẳng CB là:
A. CB = 10 cm
B. CB = 20 cm
C. CB = 30 cm
D. CB = 40 cm
Mà CA = 10 cm
Do đó CB = 10 cm.
Chọn đáp án A
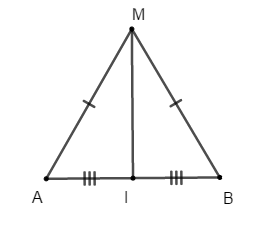
Bài 2: Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
A. Tam giác vuông
B. Tam giác cân
C. Tam giác đều
D. Tam giác vuông cân
Giả sử ΔABC có AM là trung tuyến đồng thời là đường trung trực. Ta sẽ chứng minh ΔABC là tam giác cân. Thật vậy, vì AM là trung tuyến của ΔABC (gt) ⇒ BM = MC (tính chất trung tuyến)
Vì AM là trung trực của BC ⇒ AM ⊥ BC
Xét hai tam giác vuông ΔABM và ΔACM có:
BM = CM (cmt)
AM chung
Do đó ΔABM = ΔACM (2 cạnh góc vuông)
⇒ AB = AC (2 cạnh tương ứng) ⇒ ΔABC cân tại A
Chọn đáp án B
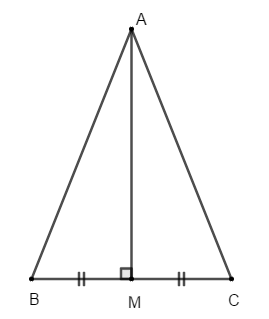
Bài 3: Cho ΔABC cân tại A , có ∠A = 40°, đường trung trực của AB cắt BC tại D . Tính ∠CAD
A. 30° B. 45° C. 60° D. 40°
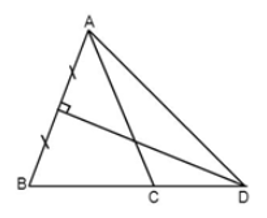

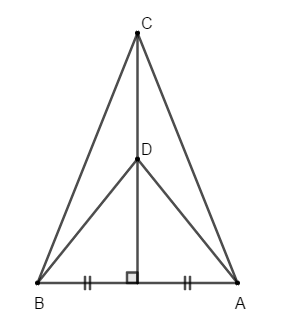
Bài 4: Cho ΔABC cân tại A. Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của ∠ACB. Tính các góc của ΔABC
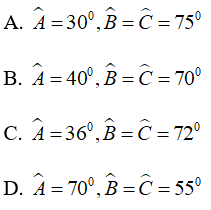
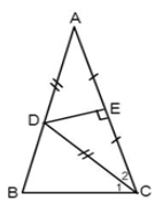
Vì đường trung trực của AC cắt AB ở D nên suy ra DA = DC (Tính chất đường trung trực của đoạn thẳng)
⇒ ΔDAC là tam giác cân tại D (dấu hiệu nhận biết tam giác cân)
Chọn đáp án C
Bài 5: Cho ΔABC vuông tại A, có ∠C = 30°, đường trung trực của BC cắt AC tại M. Em hãy chọn câu đúng:
A. BM là đường trung tuyến của ΔABC
B. BM = AB
C. BM là phân giác của ∠ABC
D. BM là đường trung trực của ΔABC
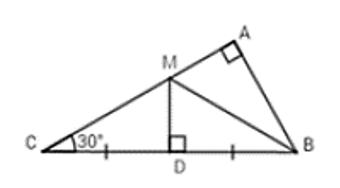
Vì M thuộc đường trung trực của BC ⇒ BM = MC (tính chất điểm thuộc đường trung trực của đoạn thẳng)
ΔBMC cân tại M (dấu hiệu nhận biết tam giác cân)

Bài 6: Chọn đáp án sai.
Cho C và D thuộc đường trung trực của đoạn thẳng AB. Khi đó ta có:
Chọn đáp án D
Bài 7: Cho tam giác ABC vuông tại A. Từ A kẻ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD. Khi đó ta có:
A. Tam giác BCD là tam giác nhọn
B. Tam giác BCD là tam giác vuông tại B
C. Tam giác BCD là tam giác vuông tại D
D. Tam giác BCD là tam giác vuông tại C
Chọn đáp án C
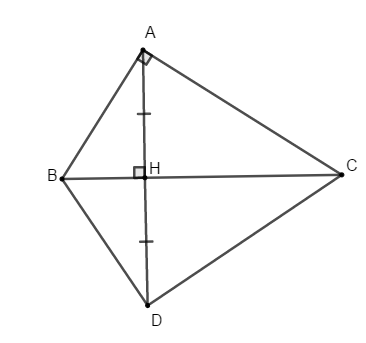
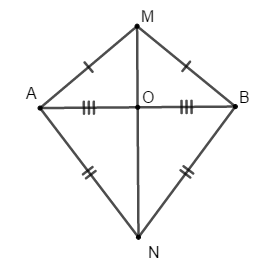
Bài 8: Cho đoạn thẳng AB. Gọi O là trung điểm của AB. Trong hai nửa mặt phẳng bờ là đường thẳng AB lấy hai điểm M và N sao cho MA = MB và NA = NB.
A. Đường thẳng MN đi qua O
B. Đường thẳng MN vuông góc với AB
C. Đường thẳng MN vuông góc với AB tại O
D. Đường thẳng MN song song với AB
Ta có: MA = MB nên M thuộc đường trung trực của đoạn thẳng AB
Tương tự NA = NB nên N thuộc đường trung trực của đoạn thẳng AB
Suy ra MN là đường trung trực của đoạn thẳng AB
Mà O là trung điểm của AB
Vậy MN vuông góc với AB tại O.
Chọn đáp án C
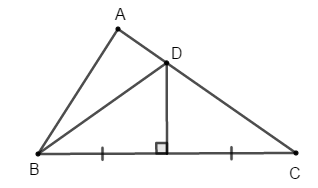
Bài 9: Cho tam giác ABC có AB = 16 cm; AC = 25 cm. Vẽ đường trung trực của BC cắt AC tại D. Chu vi tam giác ABD là:
A. 40 cm
B. 41 cm
C. 42 cm
D. 43 cm
D thuộc đường trung trực của đoạn thẳng BC nên DB = DC (tính chất điểm thuộc đường trung trực của đoạn thẳng)
Chu vi tam giác ABD là:
AB + DB + AD = AB + DC + AD = AB + (CD + AD) = AB + AC = 16 + 25 = 41 cm
Vậy chu vi tam giác ABC là 41 cm.
Chọn đáp án B
Bài 10: Cho đoạn thẳng AB có độ dài bằng 12 cm. Gọi I là trung điểm của AB. Điểm M thuộc đường trung trực của đoạn thẳng AB sao cho MA = 10 cm. Chọn câu sai trong các câu sau đây:
A. MB = 10 cm
B. MI = 8 cm
C. 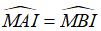
D. MA = MB = MI
Chọn đáp án D