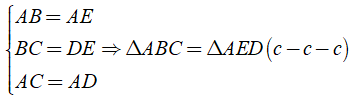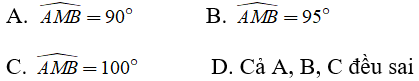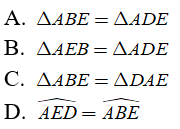Bài tập Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh (c.c.c) có lời giải - Toán lớp 7
Bài tập Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh (c.c.c) có lời giải
Với bộ Bài tập Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh (c.c.c) Toán lớp 7 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 7.

Bài 1: Cho hình vẽ sau. Tam giác nào bằng với tam giác ABC?
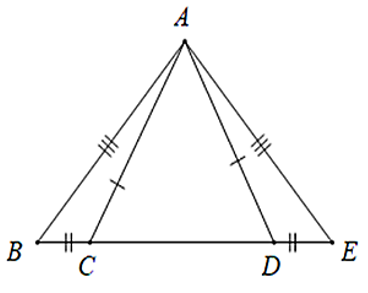
A. ΔABC = ΔEDA
B. ΔABC = ΔEAD
C. ΔABC = ΔAED
D. ΔABC = ΔADE
Ta có:
Chọn đáp án C.
Bài 2: Cho hai tam giác ABD và CDB có cạnh chung là BD. Biết AB = DC và AD = CB. Phát biểu nào sau đây sai?

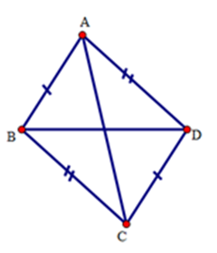
Xét ΔABC và ΔCDA có:
AB = CD (gt)
Cạnh AC chung.
AD = BC (gt)
⇒ ΔABC = ΔCDA (c - c - c)
⇒ ∠ABC = ∠CDA; ∠BAC = ∠DCA; ∠BCA = ∠DAC (góc tương ứng bằng nhau)
Vậy đáp án C sai.
Chọn đáp án C.
Bài 3: Cho hình dưới đây. Chọn đáp án sai
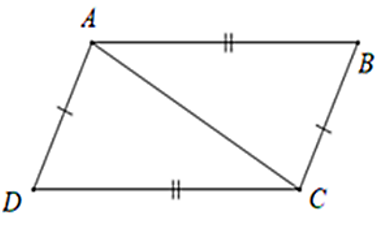
A. AD // BC
B. AB // CD
C. ΔABC = ΔCDA
D. ΔABC = ΔADC
Xét tam giác ADC và CBA ta có:
AB = CD
AD = BC
AC chung
⇒ ΔADC = ΔCBA (c-c-c)
Do đó: ∠DAC = ∠BCA (hai góc tương ứng) mà hai góc ở vị trí sole nên AD // BC
Tương tự AB // CD
Vậy đáp án A, B, C đúng và D sai.
Chọn đáp án D.
Bài 4: Cho tam giác ABD và tam giác IKH có AB = KI, AD = KH, DB = IH. Phát biểu nào sau đây đúng?
A. ΔBAD = ΔHIK
B. ΔABD = ΔKHI
c. ΔDAB = ΔHIK
D. ΔABD = ΔKIH
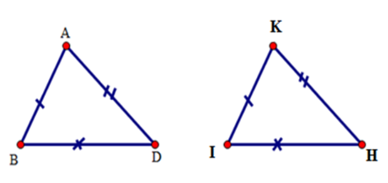
Xét tam giác ABD và tam giác KIH có AB = KI, AD = KH, DB = IH.
⇒ ΔABD = ΔKIH (c-c-c)
Chọn đáp án D.
Bài 5: Cho đoạn thẳng AB = 6cm. Trên một nửa mặt phẳng bờ AB vẽ tam giác ABC sao cho AC = 4cm, BC = 5cm, trên nửa mặt phẳng còn lại vẽ tam giác ABD sao cho BD = 4cm, AD = 5cm. Chọn đáp án đúng?
A. ΔCAB = ΔDAB
B. ΔABC = ΔBDA
C. ΔCAB = ΔDBA
D. ΔCAB = ΔABD
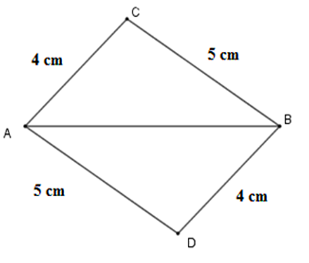
Từ bài ra ta có: AC = BD = 4cm; BC = AD = 5cm
Xét ΔCAB và ΔDBA có:
AC = BD
AB chung
BC = AD
⇒ ΔCAB = ΔDBA (c-c-c)
Chọn đáp án C.
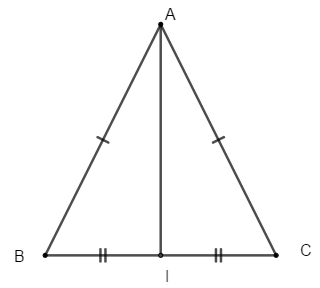
Bài 6: Cho tam giác ABC có AB = AC và I là trung điểm của BC. Khi đó:
Chọn đáp án D
Bài 7: Cho tam giác MNP và tam giác DEF có MN = ED, MP = EF và NP = DF. Phát biểu nào sau đây đúng?
A. ΔNPM = ΔFDE
B. ΔMNP = ΔFDE
C. ΔMNP = ΔEDF
D. ΔNMP = ΔEDF
Xét ΔMNP và ΔEDF có:
MN = ED (gt)
MP = EF (gt)
NP = DF (gt)
Suy ra ΔMNP = ΔEDF (c – c – c)
Chọn đáp án c
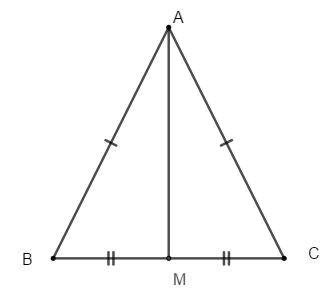
Bài 8: Cho tam giác ABC có AB = AC và M là trung điểm của BC. Tính số đo góc
Chọn đáp án A
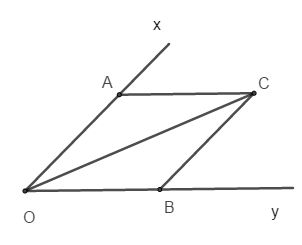
Bài 9: Cho góc xOy. Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự ở A và B. Vẽ hai cung tròn tâm A và B có cùng bán kính sao cho chúng cắt nhau tại điểm C nằm trong góc xOy.
Câu nào sau đây sai?
A. 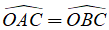
B. OC là tia phân giác của góc xOy
C. CO là tia phân giác của góc ACB
D. A, B đúng, C sai
Chọn đáp án D
Bài 10: Cho tam giác ABC có AB < AC. Điểm D thuộc AC sao cho AD = AB. Gọi E là điểm nằm trong tam giác ABC sao cho EB = ED. Khi đó
Chọn đáp án A