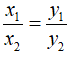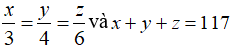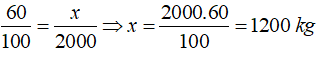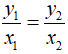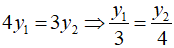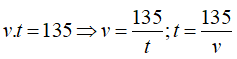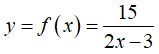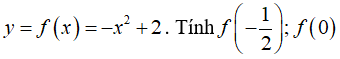Tổng hợp Trắc nghiệm Chương 2 Đại Số 7 có lời giải - Toán lớp 7
Tổng hợp Trắc nghiệm Chương 2 Đại Số 7 có lời giải
Với bộ Tổng hợp Trắc nghiệm Chương 2 Đại Số 7 Toán lớp 7 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 7.

Bài 1: Cho biết x và y là hai đại lượng tỉ lệ thuận theo hệ số -2. Hãy biểu diễn theo y theo x.
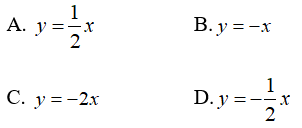
Vì x và y là hai đại lượng tỉ lệ thuận theo hệ số -2 nên y cũng tỉ lệ thuận với x theo hệ số tỉ lệ -1/2
Suy ra y = -(1/2)x
Chọn đáp án D
Bài 2: Cho biết x và y là hai đại lượng tỉ lệ thuận theo hệ số k. Khi x = 12 thì y = -3. Hệ số tỉ lệ là
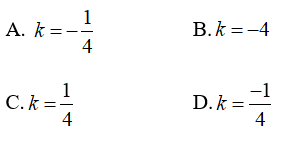
Vì x và y là hai đại lượng tỉ lệ thuận theo hệ số k nên x = ky
Ta có 12 = k.(-3) ⇒ k = -4
Hay x = (-4)y
Chọn đáp án B
Bài 3: Cho biết x và y là hai đại lượng tỉ lệ thuận theo hệ số k. Khi x = 12 thì y = -3. Công thức biểu diễn y theo x là:
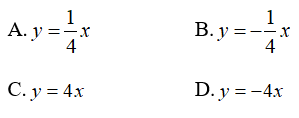
Từ câu trước ta có: x = (-4)y ⇒ y = (-1/4)x
Chọn đáp án B
Bài 4: Cho biết x và y là hai đại lượng tỉ lệ thuận theo hệ số tỉ lệ k = -3.Cho giá trị bảng sau
| x | -4 | x2 | 1 |
| y | y1 | 2/3 | y3 |
Khi đó:
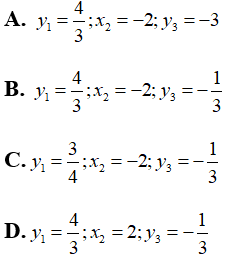
Vì x và y là hai đại lượng tỉ lệ thuận theo hệ số -3 nên x = -3y
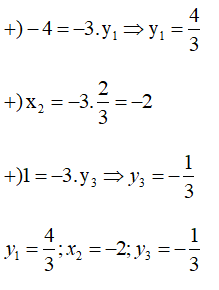
Chọn đáp án B
Bài 5: Giả sử x và y là hai đại lượng tỉ lệ thuận; x1, x2 là hai giá trị khác nhau của x và y1, y2 là hai giá trị tương ứng của y. Tính x1 biết x2 = 3, y1 = -3/5, y2 = 1/10
A. x1 = -18 B. x1 = 18 C. x1 = -6 D. x1 = 6
Vì x và y là hai đại lượng tỉ lệ thuận nên
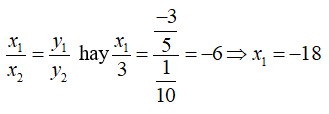
Chọn đáp án A
Bài 6: Cho hai đại lượng x và y có bảng giá trị sau:
| x | 2,3 | 4,8 | -9 | -6 | -5 |
| y | 4,8 | 2,3 | -5 | -6 | -9 |
Kết luận nào sau đây đúng
A. x và y là hai đại lượng tỉ lệ thuận với nhau theo hệ số tỉ lệ 23/48
B. x và y là hai đại lượng tỉ lệ thuận với nhau theo hệ số tỉ lệ 9/5
C. x và y không tỉ lệ thuận với nhau
D. y và x tỉ lệ thuận theo hệ số tỉ lệ 5/9
Ta thấy 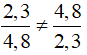
Chọn đáp án C
Bài 7: Giả sử x và y là hai đại lượng tỉ lệ thuận x1, x2; là hai giá trị khác nhau của x và y1, y2 là hai giá trị tương ứng của y. Tính x1, y1 biết 2y1 + 3x1 = 24, x2 = -6, y2 = 3
A. x1 = 12; y1 = 6
B. x1 = -12; y1 = -6
C. x1 = 12; y1 = -6
D. x1 = -12; y1 = 6
Vì x và y là hai đại lượng tỉ lệ thuận nên
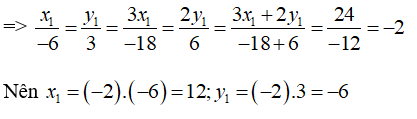
Chọn đáp án C
Bài 8: Chia số 117 thành ba phần x, y, z (0 < x, y, z < 117) tỉ lệ thuận với 3; 4; 6. Khi đó phần lớn nhất là số
A. 36 B. 54 C. 27 D. 45
Chia số 117 thành ba phần x, y, z tỉ lệ thuận với 3; 4; 6
Ta có
Áp dụng tính chất dãy tỉ số bằng nhau ta có
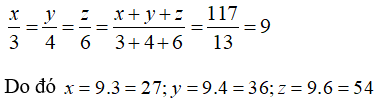
Phần lớn nhất là 54
Chọn đáp án B
Bài 9: Cứ 100kg thóc thì cho 60kg gạo. Hỏi 2 tấn thóc thì cho bao nhiêu kilogam gạo?
A. 200 kg B. 12 kg C. 120 kg D. 1200 kg
Đổi 2 tấn = 2000 kg
Gọi x (x > 0) là số kilogam gạo có trong hai tấn thóc
Ta thấy số tấn thóc và số gạo là hai đại lượng tỉ lệ thuận
Ta có
Vậy 2 tấn thóc có 1200 kg
Chọn đáp án D
Bài 10: Cho x, y là hai đại lượng tỉ lệ thuận. Biết rằng với hai giá trị x1, x2 của có tổng bằng 1 thì hai giá trị tương ứng y1, y2 có tổng bằng 5. Biểu diễn y theo x ta được
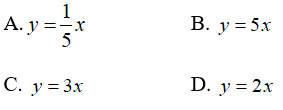
Vì x và y là hai đại lượng tỉ lệ thuận nên theo tính chất của đại lượng tỉ lệ thuận ta có
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
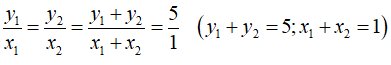
Vậy y và x tỉ lệ thuận với nhau theo hệ số tỉ lệ là 5
Suy ra y = 5x
Chọn đáp án B.
Bài 11: Khi có xy = a với a là hằng số khác 0, ta nói
A. y tỉ lệ với x
B. y tỉ lệ nghịch với x theo hệ số tỉ lệ a
C. y tỉ lệ thuận với x
D. x tỉ lệ thuận với y
Nếu đại lượng y liên hệ với đại lượng x theo công thức xy = a thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a
Chọn đáp án B
Bài 12: Cho x và y là hai đại lượng tỉ lệ nghịch và y = a/x. Gọi x1, x2, x3 là các giá trị của x và y1, y2, y3 là các giá trị tương ứng của y. Ta có:
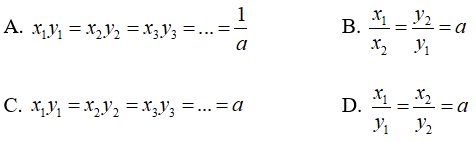
Nếu hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ a thì:
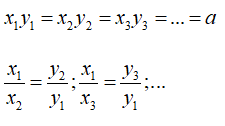
Chọn đáp án C
Bài 13: Cho bảng sau:
| x | 10 | 20 | 25 | 30 | 40 |
| y | 10 | 5 | 4 | 10/3 | 2,5 |
Khi đó:
A. y tỉ lệ với x
B. y và x là hai đại lượng tỉ lệ thuận
C. y và x là hai đại lượng tỉ lệ nghịch.
D. y và x là hai đại lượng bất kì
Xét các tích giá trị của và ta được: 10.10 = 20.5 = 25.4 = 30.(10/3) = 40.2,5 = 100
Nên y và x là hai đại lượng tỉ lệ nghịch
Chọn đáp án C
Bài 14: Cho biết x và y là hai đại lượng tỉ lệ nghịch. Khi x = 7 thì y = 4. Tìm y khi x = 5
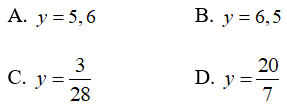
Vì x và y là hai đại lượng tỉ lệ nghịch nên ta có 7.4 = 5.y ⇒ y = 28/5 = 5,6
Chọn đáp án A
Bài 15: Cho biết x và y là hai đại lượng tỉ lệ nghịch với nhau. Khi x = -1/2 thì y = 8. Khi đó hệ số tỉ lệ a và công thức biểu diễn y theo x là:
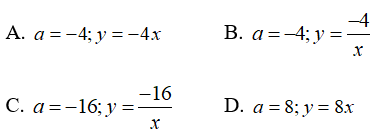
Vì x và y là hai đại lượng tỉ lệ nghịch với nhau và x = -1/2 thì y = 8
Nên hệ số tỉ lệ là a = x.y = (-1.2).8 = -4
Công thức biểu diễn y theo x là y = -4/x
Vậy a = -4 ; y = -4/x
Chọn đáp án B
Bài 16: Cho hai đại lượng tỉ lệ nghịch x và y; x1, x2 là hai giá trị khác nhau của x và y1, y2 là hai giá trị tương ứng của y. Biết x1 = 4; x2 = 3 và y1 + y2 = 14. Khi đó y2 = ?
A. y2 = 5 B. y2 = 7 C. y2 = 6 D. y2 = 8
Vì x và y là hai đại lượng tỉ lệ nghịch nên x1y1 = x2y2 mà x1 = 4; x2 = 3 và y1 + y2 = 14
Do đó
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
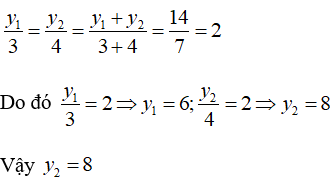
Chọn đáp án D
Bài 17: Cho hai đại lượng tỉ lệ nghịch x và y; x1, x2 là hai giá trị khác nhau của x và y1, y2 là hai giá trị tương ứng của y. Biết x2 = -4 và y1 = -10 và 3x1 - 2y2 = 32. Tính x1 và y2
A. x1 = 16; y2 = 40
B. x1 = -40; y2 = -16
C. x1 = 16; y2 = -40
D. x1 = -16; y2 = -40
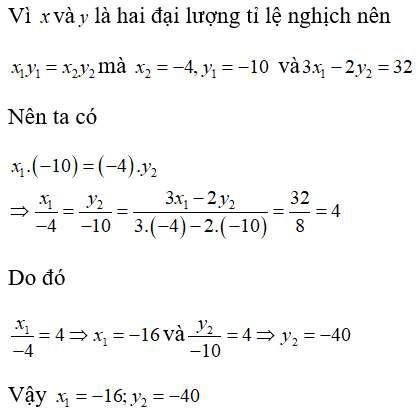
Chọn đáp án D
Bài 18: Một ô tô đi quãng đường 135 km với vận tốc v (km/h) và thời gian t (h). Chọn câu đúng về mối quan hệ của v và t
A. v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 1/135
B. v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 135
C. v và t là hai đại lượng tỉ lệ thuậnvới hệ số tỉ lệ 135
D. v và t là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ 1/135
Từ bài ra ta có:
Nên v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 135
Chọn đáp án B
Bài 19: Để làm một công việc trong 8 giờ cần 30 công nhân. Nếu có 40 công nhân thì công việc đó được hoàn thành trong mấy giờ?
A. 5 giờ B. 8 giờ C. 6 giờ D. 7 giờ
Gọi thời gian 40 công nhân làm một công việc đó là x (x > 0) (giờ)
Vì số công nhân và thời gian làm của công nhận là đại lượng tỉ lệ nghịch nên theo bài ra ta có 8.30 = 40.x ⇒ x = 240/40 = 6 giờ
Vậy 40 công nhận thì công việc đó được hoàn thành trong 6 giờ
Chọn đáp án C
Bài 20: Cho biết y tỉ lệ nghịch với x theo tỉ số k1 (k1 ≠ 0) và x tỉ lệ nghịch với z theo tỉ số k2 (k2 ≠ 0). Chọn câu đúng
A. y và z tỉ lệ nghịch với nhau theo hệ số tỉ lệ k1/k2
B. y và z tỉ lệ nghịch với nhau theo hệ số tỉ lệ k2/k1
C. y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ k1.k2
D. y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ k1/k2

Chọn đáp án D
Bài 21: Cho bảng giá trị sau. Chọn câu đúng
| x | -12 | -3 | 10 | 12 |
| y | 2 | 4 | 1 | 3 |
A. Đại lượng y là hàm số của đại lượng x
B. Đại lượng y là không hàm số của đại lượng x
C. Đại lượng y tỉ lệ thuận với đại lượng x
D. Đại lượng y tỉ lệ nghịch với đại lượng x
Từ bảng giá trị ta thấy với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x
Chọn đáp án A
Bài 22: Cho các công thức y - 3 = x; -2y = x; y2 = x. Có bao nhiêu công thức chứng tỏ rằng y là hàm số của x
A. 0 B. 1 C. 2 D. 3
Nhận thấy y - 3 = x ⇒ y = x + 3 là một hàm số
-2y = x ⇒ y = -x/2 là một hàm số
Với y2 = x ta thấy khi x = 4 thì y2 = 4 suy ra y = 2 hoặc y = -2 nên với một giá trị của x cho hai giá trị của y nên y không là hàm số của x
Chọn đáp án C
Bài 23: Cho hàm số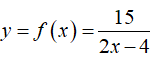
A. x ≠ 4 B. x = 4 C. x ≠ 2 D. x = 2
Hàm số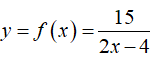
Chọn đáp án C
Bài 24: Bảng giá trị nào sau đây là đúng với hàm số


Chọn đáp án A
Bài 25: Một hàm số được cho bằng công thức
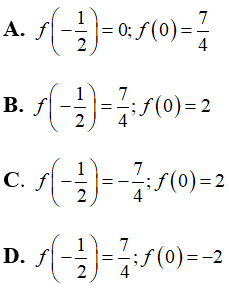
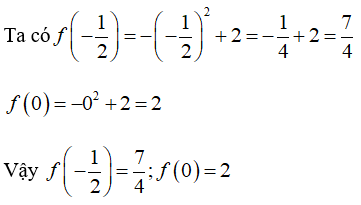
Chọn đáp án B
Bài 26: Một hàm số được cho bẳng công thức y = f(x) = x2. Tính f(5) + f(-5)
A. 0 B. 25 C. 50 D. 10
Ta có f(-5) = (-5)2 = 25 và f(5) = 52 = 25
Nên f(5) + f(-5) = 25 + 25 = 50
Chọn đáp án C
Bài 27: Tìm tọa độ điểm M trên hình vẽ sau
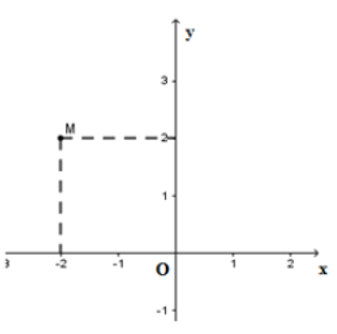
A. (-2, -2) B. (-2, 2) C. (2, -2) D. (2, 2)
Tọa độ điểm M là (-2, 2)
Chọn đáp án B
Bài 28: Điểm nào dưới đây có tọa độ (1, -3)
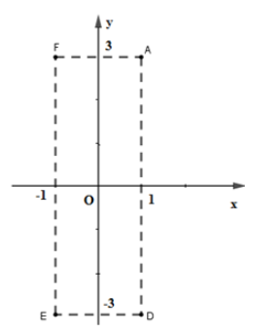
A. D B. E C. A D. F
Từ hình vẽ ta có A(1, 3) ; F(-1, 3) ; D(1, -3) ; E(-1, -3)
Nên điểm có tọa độ (1, -3) là điểm D
Chọn đáp án A
Bài 29: Trên mặt phẳng tọa độ, các điểm có hoành độ bằng 0 là
A. Nằm trên trục hoành
B. Nằm trên trục tung
C. Điểm A(0, 3)
D. Gốc tọa độ
Các điểm nằm trên trục hoành đều có tung độ bằng 0
Các điểm nằm trên trục tung đều có hoành độ bằng 0
Chọn đáp án B
Bài 30: Trong các điểm M(3, -3) ; N(4, 2) ; P(-3, -3) ; Q(-2, 1) ; H(-1, 3) có bao nhiêu điểm thuộc góc phần tư thứ hai?
A. 0 B. 1 C. 4 D. 2
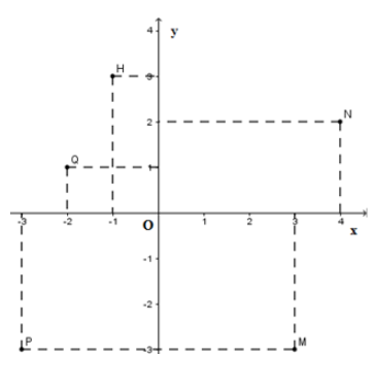
Vẽ các điểm M(3, -3) ; N(4, 2) ; P(-3, -3) ; Q(-2, 1) ; H(-1, 3) trên cùng mặt phẳng tọa độ.
Ta thấy có hai điểm thuộc góc phần tư thứ hai là Q(-2, 1) ; H(-1, 3)
Chọn đáp án D
Bài 31: Đồ thị hàm số y = ax (a ≠ 0) là:
A. Một đường thẳng
B. Đi qua gốc tọa độ
C. Một đường thẳng đi qua gốc tọa độ
D. Một đoạn thẳng đi qua gốc tọa độ
Theo định nghĩa đồ thị hàm số y = ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ
Chọn đáp án C
Bài 32: Điểm thuộc đồ thị hàm số y = -2x là:
A. M(-2, -2) B. N(1, 4) C. P(-1, -2) D. Q(-1, 2)
Thay các điểm M, N, P vào hàm số đều không thỏa mãn, chỉ có điểm Q(-1, 2) thỏa mãn vì 2 = (-2).(-1)
Chọn đáp án D
Bài 33: Đồ thị hàm số y = -5x không đi qua điểm
A. M(1, 5) B. N(-2, 10) C. P(-1, 5) D. Q(2, -10)
Thay điểm M(1, 5) vào hàm số y = -5x ta thấy 5 ≠ 1.(-5) = -5 nên đồ thị hàm số y = -5x không đi qua điểm M(1, 5)
Chọn đáp án A
Bài 34: Điểm B(-2, 6) không thuộc đồ thị hàm số
A. y = -3x B. y = x + 8 C. y = 4 - x D. y = x2
Ta thấy 6 ≠ (-2)2 = 4 nên điểm B(-2, 6) không thuộc đồ thị hàm số y = x2
Chọn đáp án D
Bài 35: Cho hàm số y = 5x. Trong các điểm A(1, 2); B(2, 10); C(-2, 10); D(-1/5, -1) có bao nhiêu điểm thuộc đồ thị hàm số y = 5x
A. 2 B. 1 C. 3 D. 4
Đặt y = f(x) = 5x
Xét A(1, 2) có x = 1; y = 2. Khi đó f(1) = 5.1 = 5 ≠ 2 tức 2 ≠ f(1)
Vậy điểm A không thuộc đồ thị hàm số y = 5x
Xét điểm B(2, 10) có x = 2, y = 10. Khi đó f(2) = 5.2 = 10 tức là 10 = f(2)
Vậy điểm B thuộc đồ thị hàm số
Tương tự ta có f(-2) = -10 ≠ 10; f(-1/5) = -1 nên C không thuộc đồ thị, điểm D thuộc đồ thị trên
Vậy có hai điểm thuộc đồ thị hàm số y = 5x là điểm B(2, 10) và D(-1/5, -1)
Chọn đáp án A
Bài 36: Đồ thị hàm số y = -4x nằm ở những góc phần tư nào của hệ trục tọa độ?
A. (I), (II) B. (II), (IV) C. (I), (III) D. (III), (IV)
Ta có đồ thị hàm số y = -4x là đường thẳng đi qua hai điểm O(0, 0), A(-1, 4) như hình vẽ
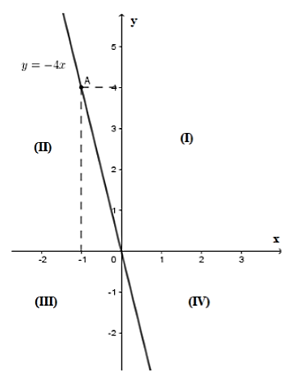
Nên đồ thị hàm số y = -4x thuộc góc phần tư thứ hai và thứ tư
Chọn đáp án B
Bài 37: Cho đồ thị hàm số y = ax (a ≠ 0) là đường thẳng OM trên hình vẽ. Khi đó hệ số a bằng
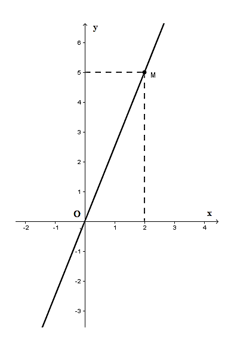
A. 5 B. 5/2 C. 2/5 D. 1
Từ đồ thị hàm số ta thấy điểm M(2, 5) thuộc đồ thị hàm số nên ta thay x = 2, y = 5 vào hàm số y = ax (a ≠ 0) ta được 5 = a.2 ⇒ a = 5/2 (TM)
Vậy a = 5/2
Chọn đáp án B
Bài 38: Trong mặt phẳng tọa độ Oxy cho đồ thị hàm số y = ax (a ≠ 0) là đường thẳng OA với điểm A(-1, -3). Hãy xác định công thức của đồ thị hàm số trên
A. y = (1/3)x B. y = 2x C. y = -3x D. y = 3x
Đồ thị hàm số y = ax (a ≠ 0) là đường thẳng OA với điểm A(-1, -3) do đó khi x = -1 thì y = -3
Nên ta có -3 = a.(-1) ⇒ a = 3 (TM)
Công thức của hàm số đã cho là y = 3x
Chọn đáp án D
Bài 39: Cho hình vẽ sau
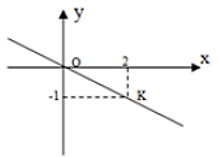
Đường thẳng OK là đồ thị hàm số nào dưới đây
A. y = -2x B. y = -0,5x C. y = (1/2)x D. y = 2x
Ta gọi hàm số cần tìm là y = ax (a ≠ 0). Khi đó thay x = 2; y = -1 vào y = ax ta được -1 = a.2 ⇒ a = -1/2
Từ hình vẽ ta thấy đồ thị hàm số đi qua điểm (2; - 1)
Nên y = -0,5x
Chọn đáp án B
Bài 40: Đồ thị của hàm số y = (1/5)x là đường thẳng OA với O(0, 0) và:
A. A(1, 5) B. A(-1, -5) C. A(5, 1) D. A(-5, 1)
Ta thấy A(5, 1) thỏa mãn hàm số y = (1/5)x vì 1 = (1/5).5 ⇔ 1 = 1 (luôn đúng)
Nên đồ thị của hàm số y = (1/5)x đi qua điểm A(5, 1)
Chọn đáp án C