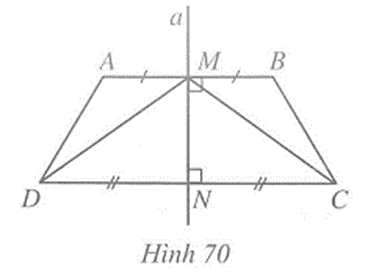
Trong Hình 70 đường thẳng a là đường trung trực của đoạn thẳng AB và CD

Trong đường thẳng a là đường trung trực của đoạn thẳng AB và CD. Chứng minh:

Giải vở bài tập Toán 7 Bài 9: Đường trung trực của một đoạn thẳng

Câu 2 trang 103 vở bài tập Toán lớp 7 Tập 2: Trong Hình 70 đường thẳng a là đường trung trực của đoạn thẳng AB và CD. Chứng minh:

a) AB // CD;

b) ∆MNC = ∆MND;

c) $\hat{AMD}$ = $\hat{BMC}$ ;

d) AD = BC, $\hat{A}$ = $\hat{B}$ ;

e) $\hat{ADC}$ = $\hat{BCD}$ .

Trong Hình 70 đường thẳng a là đường trung trực của đoạn thẳng AB và CD

Lời giải:

a) Vì a là đường trung trực của cả hai đoạn thẳng AB và CD nên AB $⊥$ a; CD $⊥$ a. Suy ra AB // CD.

b) Xét hai tam giác vuông MNC và MND, ta có:

NC = ND (giả thiết); MN là cạnh chung.

Suy ra ∆MNC = ∆MND (cạnh huyền – cạnh góc vuông).

c) Vì ∆MNC = ∆MND nên $\hat{DMN}$ = $\hat{CMN}$ (1)

Ta có: $\hat{AMD}$ và $\hat{DMN}$ , $\hat{BMC}$ và $\hat{CMN}$ là các cặp góc kề nhau; $\hat{AMN}$ = $\hat{BMN}$ = 90^o

Suy ra $\hat{AMD}$ + $\hat{DMN}$ = $\hat{AMN}$ = 90^o và $\hat{BMC}$ + $\hat{CMN}$ = $\hat{BMN}$ = 90^o

Do đó $\hat{AMD}$ = 90^o – $\hat{DMN}$ và $\hat{BMC}$ = 90^o – $\hat{CMN}$ (2)

Từ (1) và (2) suy ra $\hat{AMD}$ = $\hat{BMC}$

d) Vì ∆MNC = ∆MND nên MC = MD

Xét hai tam giác AMD và BMC, ta có:

AM = BM (giả thiết), $\hat{AMD}$ = $\hat{BMC}$ , MD = MC (chứng minh ở trên)

Suy ra ∆AMD = ∆BMC (c.g.c)

Do đó AD = BC ( hai cạnh tương ứng); $\hat{A}$ = $\hat{B}$ (hai góc tương ứng)

e) Vì ∆MNC = ∆MND nên $\hat{MCN}$ = $\hat{MDN}$ (hai góc tương ứng)

Vì ∆BMC = ∆AMD nên $\hat{BCM}$ = $\hat{ADM}$ (hai góc tương ứng)

Suy ra $\hat{MCN}$ + $\hat{BCM}$ = $\hat{MDN}$ + $\hat{ADM}$

Mà $\hat{MCN}$ và $\hat{BCM}$ , $\hat{MDN}$ và $\hat{ADM}$ là các cặp góc kề nhau nên từ đó suy ra: $\hat{ADC} = \hat{BCD}$