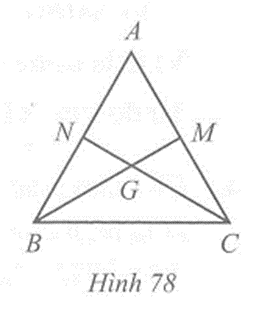
Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G

Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:

Giải vở bài tập Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác

Câu 2 trang 107 vở bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:

a) BM = CN;

b) ∆GBC cân tại G.

Lời giải:

a) Vì M, N lần lượt là trung điểm của AC và AB nên AM = $\frac{1}{2}$AC, AN = $\frac{1}{2}$AB.

Mà tam giác ABC cân tại A nên AB = AC, suy ra AM = AN.

Xét hai tam giác ABM và ACN, ta có:

AB = AC, $\hat{A}$ là góc chung, AM = AN (chứng minh trên).

Suy ra ∆ABM = ∆ACN (c.g.c)

Do đó BM = CN (hai cạnh tương ứng).

b) Vì G là trọng tâm và BM, CN là các đường trung tuyến của tam giác ABC nên GB = $\frac{2}{3}$BM, GC = $\frac{2}{3}$CN. Mà BM = CN (chứng minh trên), suy ra GB = GC

Do đó ∆GBC cân tại G