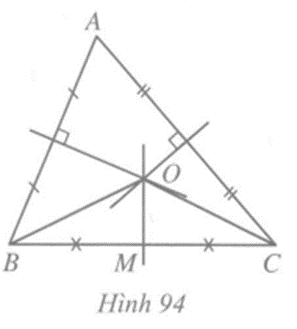
Tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại O

Tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại O nằm trong tam giác. M là trung điểm của BC. Chứng minh:

Giải vở bài tập Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác

Câu 5 trang 117 vở bài tập Toán lớp 7 Tập 2: Tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại O nằm trong tam giác. M là trung điểm của BC. Chứng minh:

a) OM $\perp$ BC;

b) $\widehat{MOB}$ = $\widehat{MOC}$.

Lời giải:

a) Vì ba đường trung trực của tam giác ABC cùng đi qua một điểm nên giao điểm O của hai đường trung trực của các cạnh AB và AC cũng thuộc đường trung trực của cạnh BC.

Vì BM = CM nên M thuộc đường trung trực của đoạn thẳng BC.

Suy ra OM là trung trực của đoạn thẳng BC hay OM ⊥ BC.

b) Xét hai tam giác vuông OMB và OMC, ta có

OM là cạnh chung, MB = MC (giả thiết)

Suy ra ∆OMB = ∆OMC (hai cạnh góc vuông).

Do đó $\widehat{MOB}$ = $\widehat{MOC}$ (hai góc tương ứng).