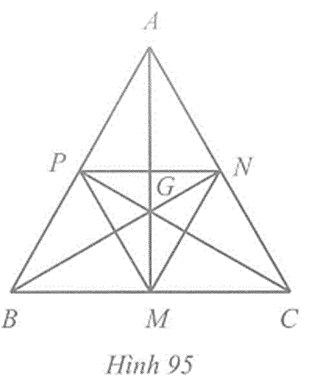
Tam giác ABC có ba đường trung tuyến AM, BN, CP cắt nhau tại G

Tam giác ABC có ba đường trung tuyến AM, BN, CP cắt nhau tại G. Biết rằng G cũng là giao điểm ba đường trung trực của tam giác MNP. Chứng minh tam giác ABC đều.

Giải vở bài tập Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác

Câu 6 trang 117 vở bài tập Toán lớp 7 Tập 2: Tam giác ABC có ba đường trung tuyến AM, BN, CP cắt nhau tại G. Biết rằng G cũng là giao điểm ba đường trung trực của tam giác MNP. Chứng minh tam giác ABC đều.

Lời giải:

Do G là giao điểm các đường trung trực của tam giác MNP nên GM = GN = GP.

Do G là trọng tâm tam giác ABC nên GA = 2GM, GB = 2GN, GC = 2GP

Suy ra GA = GB = GC.

Do GB = GC, MB = MC nên GM là đường trung trực của đoạn thẳng BC. Mà A thuộc đường thẳng GM nên AB = AC.

Do GC = GA, NC = NA nên GN là đường trung trực của đoạn thẳng CA. Mà B thuộc đường thẳng GN nên BA = BC

Suy ra AB = AC = BC. Vậy tam giác ABC là tam giác đều.