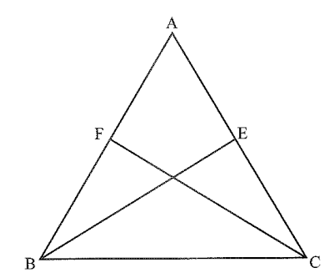
Cho tam giác ABC, có BE vuông góc với AC và CF vuông góc với AB

Cho tam giác ABC, có BE vuông góc với AC và CF vuông góc với AB. Cho biết góc FCB = góc EBC. Chứng minh góc ABC = góc ACB.

Giải vở thực hành Toán 7 Bài 2: Tam giác bằng nhau

Bài 5 trang 39 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC, có BE vuông góc với AC và CF vuông góc với AB. Cho biết góc FCB = góc EBC. Chứng minh góc ABC = góc ACB.

Lời giải:

Xét ∆ EBC vuông tại E và ∆ FCB vuông tại F.

Theo giả thiết ta có: góc FCB = góc EBC.

BC là cạnh chung.

Vậy, hai tam giác vuông EBC và FCB bằng nhau theo trường hợp cạnh huyền và một góc nhọn.

Suy ra, góc FBC = góc ECB hay góc ABC = góc ACB.