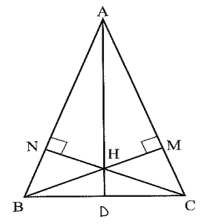
Hai đường cao BM và CN của tam giác nhọn ABC cân tại A cắt nhau ở H

Hai đường cao B và CN của tam giác nhọn ABC cân tại A cắt nhau ở H. Chứng minh đường thẳng AH đi qua trung điểm của BC.

Giải vở thực hành Toán 7 Bài 8: Tính chất ba đường cao của tam giác

Bài 7 trang 59 Vở thực hành Toán 7 Tập 2: Hai đường cao BM và CN của tam giác nhọn ABC cân tại A cắt nhau ở H. Chứng minh đường thẳng AH đi qua trung điểm của BC.

Lời giải:

Vì ba đường cao giao nhau tại một điểm nên AH vuông góc với BC.

Gọi D là giao điểm của AH với BC.

Xét tam giác ADB vuông tại D và tam giác ADC vuông tại D.

AB = AC ( do tam giác ABC cân tại A).

Cạnh chung AD.

Vậy tam giác ADB bằng tam giác ADC theo trường hợp cạnh huyền – cạnh góc vuông.

Suy ra BD = CD. Như vậy D là trung điểm của BC hay đường thẳng AH đi qua trung điểm của BC.