Giải Vở thực hành Toán 7 trang 60 Tập 2 Chân trời sáng tạo
Với Giải VTH Toán 7 trang 60 Tập 2 trong Bài 9: Tính chất ba đường phân giác của tam giác Vở thực hành Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 60.
Giải VTH Toán 7 trang 60 Tập 2 Chân trời sáng tạo
Câu 1 trang 60 Vở thực hành Toán 7 Tập 2: Khẳng định nào sau đây là đúng?
A. Đường phân giác của tam giác xuất phát từ một đỉnh chia cạnh đối diện thành hai phần bằng nhau;
B. Đường phân giác của tam giác phát xuất từ một đỉnh vuông góc với cạnh đối diện;
C. Đường phân giác đi qua trung điểm và vuông góc với cạnh đó;
D. Cho tam giác ABC, tia phân giác của góc A cắt cạnh BC tại D. Khi đó AD được gọi là đường phân giác cuả tam giác ABC.
Lời giải:
Theo định nghĩa về đường phân giác của tam giác, khi cho tam giác ABC, tia phân giác của góc A cắt cạnh BC tại D. Khi đó AD được gọi là đường phân giác của tam giác ABC.
Chọn đáp án D.
Câu 2 trang 60 Vở thực hành Toán 7 Tập 2: Khẳng định nào sau đây là đúng?
A. Ba đường phân giác giao nhau tại một điểm, điểm đó cách đều ba đỉnh của tam giác.
B. Ba đường phân giác giao nhau tại một điểm, điểm đó cách đều ba cạnh của tam giác.
C. Ba đường phân giác không đồng quy.
D. Ba đường cao của tam giác có thể giao nhau tại một điểm nằm trên cạnh của tam giác.
Lời giải:
Ta có định lí về tính chất ba đường phân giác của tam giác: Ba đường phân giác giao nhau tại một điểm, điểm đó cách đều ba cạnh của tam giác.
Chọn đáp án B.
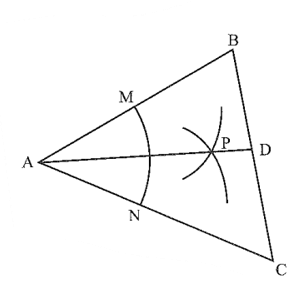
Bài 1 trang 60 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC như hình bên dưới. Kẻ đường tròn tâm A cắt AB tại M và AC tại N. Từ M và N kẻ hai cung tròn có cùng bán kính cắt nhau tại P. Đường thẳng AP cắt BC tại D. Chứng minh AD là đường phân giác của góc A.
Lời giải:
Theo đề bài, đường tròn tâm A cắt AB và AC lần lượt tại M và N, suy ra AM = AN.
Từ M và N kẻ hai cung tròn có cùng bán kính cắt nhau tại P, ta được MP = NP.
Xét tam giác AMP và tam giác ANP
AM = AN.
MP = NP.
Chung AP.
Vậy tam giác AMP bằng tam giác ANP theo trường hợp c.c.c.
Suy ra hay .
Như vậy AD là đường phân giác của góc A.
Lời giải Vở thực hành Toán 7 Bài 9: Tính chất ba đường phân giác của tam giác Chân trời sáng tạo hay khác: