Giải Vở thực hành Toán 7 trang 61 Tập 2 Chân trời sáng tạo

---

Với Giải VTH Toán 7 trang 61 Tập 2 trong Bài 9: Tính chất ba đường phân giác của tam giác Vở thực hành Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 61.

Giải VTH Toán 7 trang 61 Tập 2 Chân trời sáng tạo

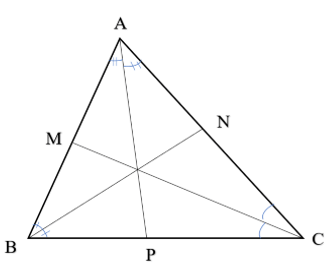
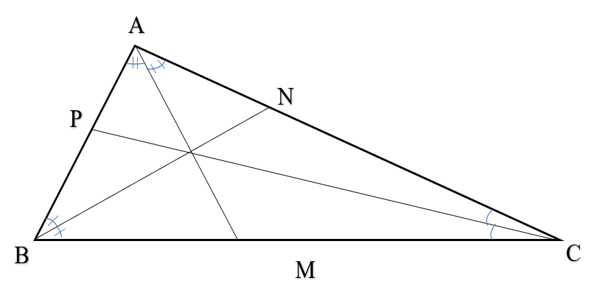
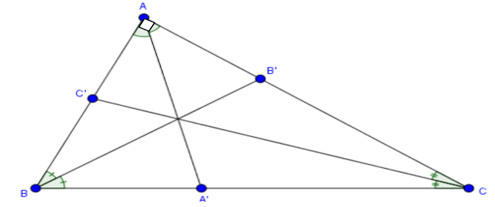
Bài 2 trang 61 Vở thực hành Toán 7 Tập 2: Vẽ ba tam giác nhọn, tù, vuông và với mỗi tam giác, vẽ ba đường phân giác của chúng.

Lời giải:

Tam giác nhọn ABC có các đường phân giác AP, CM, CN.

Tam giác tù ABC các đường phân giác AM, BN, CP.

Tam giác AOB vuông tại A có các đườnng phân giác AA’, BB’, CC’.

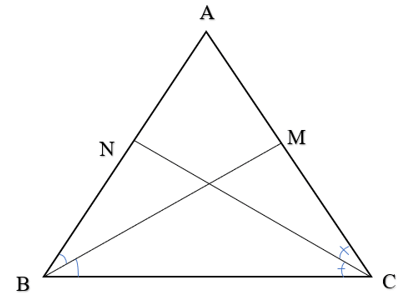
Bài 3 trang 61 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC cân tại A có BM, CN là hai đường phân giác. Chứng minh BM = CN.

Lời giải:

Tam giác ABC cân tại A nên $\widehat{\text{ABC}}=\widehat{\text{ACB}}$và AC = AB.

BM là đường phân giác của tam giác ABC nên $\widehat{\text{ABM}}=\frac{1}{2}\widehat{\text{ABC}}\text{}$.

CN là đường phân giác của tam giác ABC nên $\widehat{\text{ACN}}=\frac{1}{2}\widehat{\text{ACB}}\text{}$.

Suy ra $\widehat{\text{ABM}}\text{}$= $\widehat{\text{ACN}}$.

Xét tam giác ABM và tam giác ACN.

AB = AC.

Chung góc A.

$\widehat{\text{ABM}}\text{}$= $\widehat{\text{ACN}}$.

Vậy tam giác ABM bằng tam giác ACN theo trường hợp g.c.g. Suy ra BM = CN.

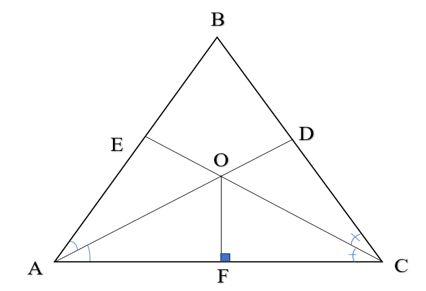
Bài 4 trang 61 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC cân tại B, hai đường phân giác AD và CE cắt nhau tại O. Từ O kẻ đường thẳng OF vuông góc với AC ( F thuộc đoạn thẳng AC). Chứng minh BF cũng là đường phân gác của góc B.

Lời giải:

Trong tam giác ABC, hai đường phân giác AD và CE cắt nhau tại O nên O là giao điểm ba đường phân giác của tam giác ABC ( tính chất ba đường phân giác của tam giác). Suy ra BO cũng là đường phân giác của tam giác ABC.

Kéo dài BO cắt AC tại F’ ta có $\widehat{\text{ABF'}}=\widehat{\text{CBF'}}$. Xét tam giác ABF’ và CBF’.

AB = CB ( do tam giác ABC cân tại B).

$\widehat{\text{ABF'}}=\widehat{\text{CBF'}}$.

Cạnh chung BF’.

Vậy tam giác ABF’ bằng tam giác CBF’ theo trường hợp c.g.c. Suy ra $\widehat{\mathrm{BF}\text{'}A}=\widehat{\text{BF'C}}$ (hai góc tương ứng) mà $\widehat{\mathrm{BF}\text{'}A}+\widehat{\text{BF'C}}=180°$ nên $\widehat{\mathrm{BF}\text{'}A}=\widehat{\text{BF'C}}=90°$ hay BF’ ⊥ AC hay OF’ ⊥ AC.

Theo đề bài OF ⊥ AC, nên F’ trùng với F.

Vậy BF cũng là đường phân giác của góc B.

Lời giải Vở thực hành Toán 7 Bài 9: Tính chất ba đường phân giác của tam giác Chân trời sáng tạo hay khác:

• Giải VTH Toán 7 trang 60 Tập 2

• Giải VTH Toán 7 trang 62 Tập 2

• Giải VTH Toán 7 trang 63 Tập 2