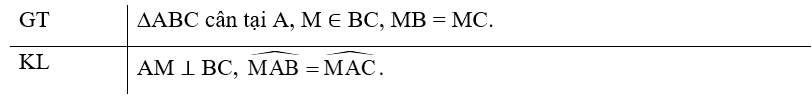Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC

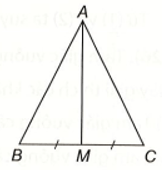
Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.

Giải Vở thực hành Toán 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

Bài 2 (4.24) trang 73 vở thực hành Toán lớp 7 Tập 1: Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.

Lời giải:

Xét tam giác ABM và tam giác ACM, ta có:

AB = AC (do ∆ABC cân tại A)

$\widehat{ABM}=\widehat{ACM}$ (do ∆ABC cân tại A)

MB = MC (theo giả thiết)

Vậy ∆ABM = ∆ACM (c – g – c)

Do đó $\widehat{MAB}=\widehat{MAC}$ (2 góc tương ứng), hay AM là tia phân giác của góc BAC.

Đồng thời $\widehat{AMB}=\widehat{AMC}=\frac{\widehat{AMB}+\widehat{AMC}}{2}=\frac{180°}{2}=90°$, hay AM ⊥ BC.