Gọi AI và AM lần lượt là đường cao và đường trung tuyến

Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng:

Giải vở thực hành Toán 7 Bài tập cuối chương 9

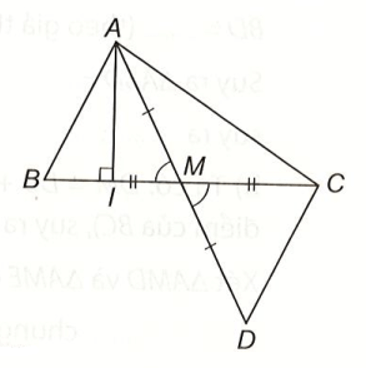
Bài 3 (9.38) trang 87 vở thực hành Toán lớp 7 Tập 2: Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng:

a) AI < $\frac{1}{2}$(AB + AC);

b) AM < $\frac{1}{2}$(AB + AC).

Lời giải:

a) Trong tam giác vuông ABI có AB là cạnh huyền nên AI < AB.

Trong tam giác vuông ACI có AC là cạnh huyền nên AI < AC.

Suy ra 2AI < AB + AC hay AI < $\frac{1}{2}$(AB + AC).

b) Lấy điểm D sao cho M là trung điểm của AD.

Xét ∆ABM và ∆DCM có: BM = CM; AM = MD; $\widehat{AMB}=\widehat{CMD}$,

do đó ∆ABM = ∆DCM (c.g.c). Suy ra AB = CD.

Trong tam giác ACD, ta có AD < CD + AC hay 2AM < AB + AC.

Suy ra AM < $\frac{1}{2}$(AB + AC).