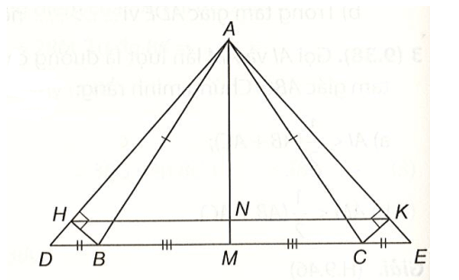
Cho tam giác ABC cân tại A. Trên tia đối của tia BC và tia đối của tia CB
Cho tam giác ABC cân tại A. Trên tia đối của tia BC và tia đối của tia CB theo thứ tự lấy hai điểm D và E sao cho BD = CE.
Giải vở thực hành Toán 7 Bài tập cuối chương 9
Bài 5 trang 88 vở thực hành Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A. Trên tia đối của tia BC và tia đối của tia CB theo thứ tự lấy hai điểm D và E sao cho BD = CE.
a) Chứng minh ∆ADE cân.
b) Gọi M là trung điểm của BC. Chứng minh AM là tia phân giác của góc DAE và AM ⊥ DE.
c) Từ B và C kẻ BH, CK theo thứ tự vuông góc với AD, AE. Chứng minh: BH = CK.
d) Chứng minh: HK // BC.
Lời giải:
a) Do ∆ABC cân tại A nên suy ra (cùng bù với góc , ).
Xét ∆ABD và ∆ACE có:
AB = AC (do tam giác ABC cân tại A)
(chứng minh trên),
BD = CE (theo giả thiết).
Suy ra ∆ABD = ∆ACE (c.g.c), do đó AD = AE (hai cạnh tương ứng), suy ra tam giác ADE cân tại A.
b) Ta có: DM = DB + BM, EM = EC + CM, mà BD = CE (gt), BM = CM (M là trung điểm của BC), suy ra DM = EM.
Xét ∆AMD và ∆AME có:
AM chung,
AD = AE (chứng minh trên),
DM = EM (chứng minh trên).
Do đó ∆AMD = ∆AME (c.c.c), suy ra và , suy ra AM là phân giác của góc DAE.
Mặt khác do và là hai góc bù nhau nên = 90° hay AM ⊥ DE.
c) Vì ∆ABD = ∆ACE (chứng minh trên) nên .
Xét tam giác vuông ABH và tam giác vuông ACK, ta có:
AB = AC (do tam giác ABC cân tại A); , do đó ∆ABH = ∆ACK (cạnh huyền – góc nhọn), suy ra BH = CK (hai cạnh tương ứng).
d) Gọi giao điểm của AM và HK là N.
Xét ∆ANH và ∆ANK, có: AH = AK (do ∆ABH = ∆ACK), (chứng minh trên), AN là cạnh chung. Do đó ∆ANH = ∆ANK, suy ra (hai góc tương ứng), mà hai góc này bù nhau nên = 90°, suy ra AM ⊥ HK.
Ta có AM ⊥ HK, mà AM ⊥ BC (do AM ⊥ DE) nên HK // BC.