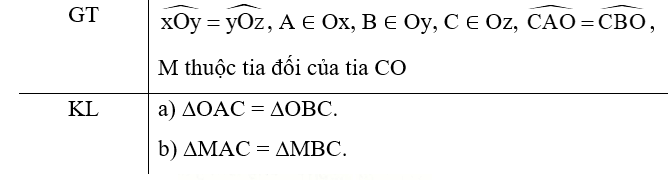Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz

Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho

Giải Vở thực hành Toán 7 Luyện tập chung trang 66, 67, 68

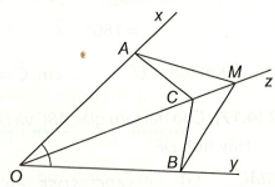
Bài 4 (4.19) trang 67 vở thực hành Toán lớp 7 Tập 1: Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho $\widehat{CAO}=\widehat{CBO}.$

a) Chứng minh rằng ∆OAC = ∆OBC.

b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng ∆MAC = ∆MBC.

Lời giải:

a) Xét hai tam giác OAC và OBC, ta có:

$\widehat{COA}=\widehat{COB}$ (OC là tia phân giác của góc AOB);

OC là cạnh chung;

$\widehat{ACO}=180°-\widehat{CAO}-\widehat{COA}$

$=180°-\widehat{CBO}-\widehat{COB}=\widehat{BCO}$

Vậy ∆OAC = ∆OBC (g – c – g).

b) Xét hai tam giác MAC và MBC có:

C A= CB (do ∆OAC = ∆OBC),

$\widehat{MCA}=180°-\widehat{ACO}=180°-\widehat{BCO}=\widehat{MCB}$ (do ∆OAC = ∆OBC),

MC là cạnh chung.

Vậy ∆MAC = ∆MBC (c – g – c).