Cho hình thang ABCD (AB song song CD). Kẻ đường thẳng vuông góc với AC tại C

Giải vở thực hành Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

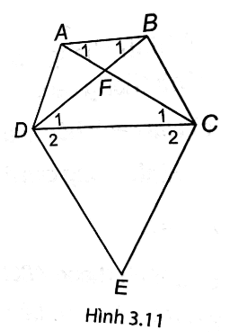
Bài 3 trang 48 vở thực hành Toán 8 Tập 1: Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.

Lời giải:

(H.3.11). Ta có EC = ED nên tam giác ECD cân tại E, suy ra ${\widehat{D}}_2={\widehat{C}}_2.$ (1)

Do AC ⊥ CE, BD ⊥ DE nên ${\widehat{D}}_1+{\widehat{D}}_2=\widehat{BDE}=90°,$ ${\widehat{C}}_1+{\widehat{C}}_2=\widehat{ACE}=90°.$ (2)

Gọi F là giao điểm của AC và BD.

Từ (1) và (2) suy ra ${\widehat{D}}_1={\widehat{C}}_1$ ⇒ ∆DCF cân tại F ⇒ DF = CF (3)

Do AB // CD nên ${\widehat{D}}_1={\widehat{B}}_1,{\widehat{C}}_1={\widehat{A}}_1$ (hai góc so le trong).

$\Rightarrow {\widehat{A}}_1={\widehat{B}}_1$ ⇒ ∆ABF cân tại F ⇒ AF = BF (4)

Từ (3) và (4) suy ra AC = AF + CF = BF + DF = BD.

Suy ra hình thang ABCD có hai đường chéo bằng nhau nên nó là hình thang cân.

Lời giải vở thực hành Toán 8 Bài 11: Hình thang cân hay khác:

• Câu 1 trang 47 vở thực hành Toán 8 Tập 1: Điền cụm từ thích hợp vào chỗ trống. a) Hình thang cân là ...

• Câu 2 trang 47 vở thực hành Toán 8 Tập 1: Cho hình thang ABCD cân (AB // CD) có $\widehat{C}=60°$ (H.3.7). ...

• Câu 3 trang 47 vở thực hành Toán 8 Tập 1: Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho ...

• Bài 1 trang 48 vở thực hành Toán 8 Tập 1: Hình thang trong Hình 3.9 có là hình thang cân không? Vì sao? ...

• Bài 2 trang 48 vở thực hành Toán 8 Tập 1: Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD ...

• Bài 4 trang 49 vở thực hành Toán 8 Tập 1: Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I ...

• Bài 5 trang 49 vở thực hành Toán 8 Tập 1: Cho hình thang cân ABCD có đáy nhỏ BC. Hạ BH ⊥ AD, CE ⊥ AD ...