Hình thang cân ABCD (AB song song CD, AB nhỏ hơn CD) có các đường thẳng AD
Giải vở thực hành Toán 8 Bài 11: Hình thang cân - Kết nối tri thức
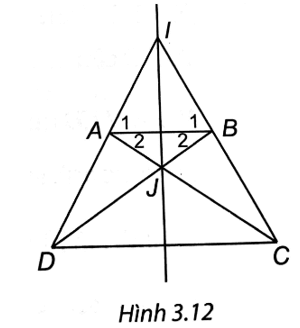
Bài 4 trang 49 vở thực hành Toán 8 Tập 1: Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.
Lời giải:
(H.3.12). Hình thang ABCD cân nên ta có AD = BC, AC = BD.
Suy ra nên tam giác IAB cân tại I, do đó IA = IB hay I cách đều đoạn thẳng AB.
Xét ∆ABD = ∆BAC có: AD = BC, AB chung, BD = AC.
Do đó ∆ABD = ∆BAC (c.c.c), suy ra nên tam giác JAB cân tại J, do đó JA = JB hay J cách đều đoạn thẳng AB.
Vậy I, J nằm trên đường trung trực của AB hay đường thẳng IJ là đường trung trực của đoạn AB.
Lời giải vở thực hành Toán 8 Bài 11: Hình thang cân hay khác: