Cho dây AB không qua tâm của đường tròn (O). Gọi A' và B' là hai điểm lần lượt đối xứng
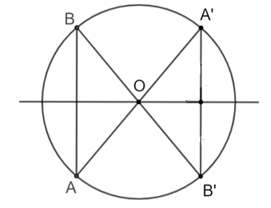
Cho dây AB không qua tâm của đường tròn (O). Gọi A' và B' là hai điểm lần lượt đối xứng với A và B qua O. Hỏi đường trung trực của A'B' có phải là trục đối xứng của (O) hay không? Tại sao?
Giải vở thực hành Toán 9 Luyện tập chung trang 107 - Kết nối tri thức
Bài 1 trang 107 VTH Toán 9 Tập 1: Cho dây AB không qua tâm của đường tròn (O). Gọi A' và B' là hai điểm lần lượt đối xứng với A và B qua O. Hỏi đường trung trực của A'B' có phải là trục đối xứng của (O) hay không? Tại sao?
Lời giải:
Do tính đối xứng tâm của (O) nên A' và B' cũng thuộc (O).
Do đó OA = OB = OA' = OB', suy ra đường trung trực của A'B' đi qua O.
Vậy đường trung trực của A'B' là trục đối xứng của (O).
Lời giải vở thực hành Toán 9 Luyện tập chung trang 107 hay khác: