Cho tam giác đều ABC có AB = 2.căn bậc hai 3. Nửa đường tròn đường kính BC cắt hai cạnh AB

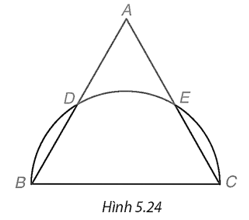
Cho tam giác đều ABC có cm. Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C) (H.5.24).

Giải vở thực hành Toán 9 Luyện tập chung trang 107 - Kết nối tri thức

Bài 6 trang 110 VTH Toán 9 Tập 1: Cho tam giác đều ABC có $AB=2\sqrt{3}$ cm. Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C) (H.5.24).

a) Chứng tỏ rằng ba cung nhỏ BD, DE và EC bằng nhau. Tính số đo mỗi cung ấy.

b) Tính diện tích của hình viên phân giới hạn bởi dây BD và cung nhỏ BD.

Lời giải:

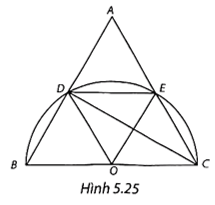
(H.5.25)

a) Gọi O là trung điểm của BC.

Tam giác DBC có đường trung tuyến OD bằng OB và OC (bằng $\frac{1}{2}BC$ ) nên DBC là tam giác vuông tại D.

Do đó, CD là đường cao của tam giác đều ABC, suy ra D là trung điểm của AB.

Tương tự, E là trung điểm của AC.

Từ đó suy ra bốn tam giác ADE, OEC, OBD, ODE là những tam giác đều, với độ dài cạnh bằng một nửa cạnh của tam giác đều ABC, tức là bằng $\frac{2\sqrt{3}}{2}=\sqrt{3}$ cm.

Ba cung nhỏ $\stackrel{⏜}{BD},$ $\stackrel{⏜}{DE}$ và $\stackrel{⏜}{EC}$ lần lượt bị chắn bởi các góc ở tâm $\widehat{BOD},$ $\widehat{DOE}$ và $\widehat{EOC}$ mà các góc này đều bằng 60° (các góc của tam giác đều) nên các cung đang xét đều bằng nhau và cùng có số đo bằng 60°.

b) Diện tích hình quạt tròn ứng với cung BD là

$S_q=\frac{60}{360}\pi {\left(\sqrt{3}\right)}^2=\frac{\pi }{2}$ (cm²).

Diện tích của tam giác BOD là

$S_{BOD}=\frac{1}{2}{\left(\sqrt{3}\right)}^2.\sin 60°=\frac{3\sqrt{3}}{4}$ (cm²).

Diện tích của hình viên phân là

$S=S_q-S_{BOD}=\frac{\pi }{2}-\frac{3\sqrt{3}}{4}\approx 0,27$ (cm²).

Lời giải vở thực hành Toán 9 Luyện tập chung trang 107 hay khác:

• Bài 1 trang 107 VTH Toán 9 Tập 1: Cho dây AB không qua tâm của đường tròn (O). Gọi A' và B' là hai điểm lần lượt đối xứng ...

• Bài 2 trang 108 VTH Toán 9 Tập 1: Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc ...

• Bài 3 trang 108 VTH Toán 9 Tập 1: Có thể xem guồng nước (còn gọi là cọn nước) là một công cụ hay cỗ máy có dạng hình tròn ...

• Bài 4 trang 109 VTH Toán 9 Tập 1: Cho đường tròn (O; 5 cm) ...

• Bài 5 trang 109 VTH Toán 9 Tập 1: Ba bộ phận truyền chuyển động của một chiếc xe đạp gồm một giò đĩa ...

• Bài 7 trang 111 VTH Toán 9 Tập 1: Cho đường tròn (O), đường kính $AB=4\sqrt{3}$ cm. Điểm C thuộc đường tròn tâm O ...