Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc
Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng:
Giải vở thực hành Toán 9 Luyện tập chung trang 107 - Kết nối tri thức
Bài 2 trang 108 VTH Toán 9 Tập 1: Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng:
a) Đường tròn đường kính BC đi qua các điểm H và K;
b) KH < BC.
Lời giải:
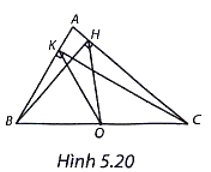
(H.5.20)
a) Gọi O là trung điểm của BC.
Do nên trong các tam giác BHC và BKC có đường trung tuyến bằng cạnh huyền.
Ta có:
Do đó, đường tròn đường kính BC đi qua các điểm H và K.
b) Theo câu a, HK là dây cung của đường tròn đường kính BC. Do đó KH < BC.
Lời giải vở thực hành Toán 9 Luyện tập chung trang 107 hay khác: