Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB
Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).
Giải vở thực hành Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn - Kết nối tri thức
Bài 3 trang 113 VTH Toán 9 Tập 1: Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).
Lời giải:
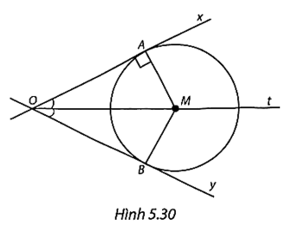
(H.5.30)
Theo đề bài, ta có Ox ⊥ MA tại A nên Ox là tiếp tuyến của (M) tại A.
Do Ot là tia phân giác của góc xOy và M ∈ Ot nên MA = MB.
Hai tam giác OMA và OMB có:
Cạnh OM chung; MA = MB;
Do đó ∆OMA = ∆OMB (c.g.c).
Suy ra tức là Oy ⊥ MB tại B.
Do vậy OB là tiếp tuyến của (M) tại B (theo dấu hiệu nhận biết tiếp tuyến).
Lời giải vở thực hành Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn hay khác: