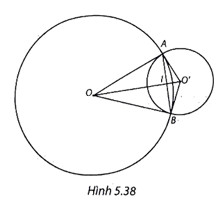
Cho hai đường tròn (O; R) và (O'; r) với R = 12 cm, r = 5 cm, OO' = 13 cm
Cho hai đường tròn (O; R) và (O'; r) với R = 12 cm, r = 5 cm, OO' = 13 cm.
Giải vở thực hành Toán 9 Bài 17: Vị trí tương đối của hai đường tròn - Kết nối tri thức
Bài 5 trang 118 VTH Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O'; r) với R = 12 cm, r = 5 cm, OO' = 13 cm.
a) Chứng minh hai đường tròn (O) và (O') cắt nhau tại hai điểm A, B và OO' là đường trung trực của AB.
b) Chứng minh AO là tiếp tuyến của đường tròn (O'; r).
Lời giải:
(H.5.38)
a) Vì 12 – 5 = 7 < 13 < 12 + 5 = 17 nên R – r < OO' < R + r.
Vậy hai đường tròn (O) và (O') cắt nhau tại hai điểm A, B.
Ta có: OA = OB = R và O'A = O'B = r nên OO' là đường trung trực của AB.
b) Ta có: nên tam giác AOO' vuông tại A (theo định lí Pythagore đảo), suy ra OA ⊥ O'A tại A.
Do đó OA là tiếp tuyến của (O'; r).
Lời giải vở thực hành Toán 9 Bài 17: Vị trí tương đối của hai đường tròn hay khác: